Bucky Balls and Phi

Bucky balls are based on sixty coordinates all based on phi.

Bucky balls are named after Buckminster Fuller, who popularized the geodesic dome.  The shape defined by Bucky balls is also found in the Carbon 60 molecule, a form of pure carbon with 60 atoms in a nearly spherical configuration, the truncated icosahedron and soccer balls.

Bucky balls consist of 60 points on the surface of a spherical shape where the distance from any point to its nearest neighboring three points on the sphere is identical for all points.

Bucky ball

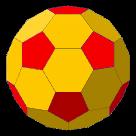
Truncated
icosahedron

Soccer ball
(A very phine sport)

Geodesic dome

Note that the surface consists of twelve phi-based pentagons, each one of which is connected to five of the twenty hexagons, shown unfolded below:

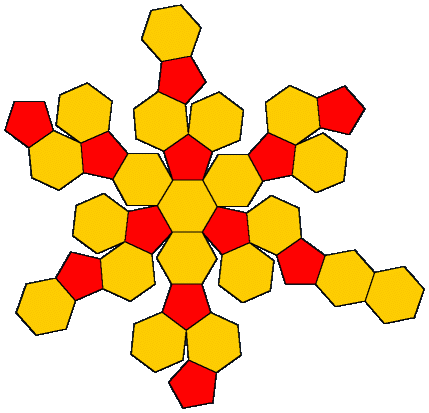
In the geodesic dome, each pentagon and hexagon is divided into identically shaped triangles, bringing the shape closer yet to a sphere.

The coordinates of the 60 vertices of a Bucky ball centered on the origin of a 3D axis are all based on phi!

These coordintates are the same as the corners of the following three rectangles shown on the Geometry page:

(0,+-1,+-3Φ), (+-1,+-3Φ,0), (+-3Φ,0,+-1)

They also can be defined by the following six 3D bricks:

(+-2,+-(1+2Φ),+-Φ)

(+-(1+2Φ),+-Φ,+-2)

(+-Φ,+-2,+-(1+2Φ))

(+-1,+-(2+Φ),+-2Φ)

(+-(2+Φ),+-2Φ,+-1)

(+-2Φ,+-1,+-(2+Φ))

Here is a complete list of all the coordinates:

(0,1,3Φ)

(0,1,-3Φ)

(0,-1,3Φ)

(0,-1,-3Φ)

 

(1,3Φ,0)

(1,-3Φ,0)

(-1,3Φ,0)

(-1,-3Φ,0)

 

(3Φ,0,1)

(3Φ,0,-1)

(-3Φ,0,1)

(-3Φ,0,-1)

 

(2,(1+2Φ),Φ)

(2,(1+2Φ),-Φ)

(2,-(1+2Φ),Φ)

(2,-(1+2Φ),-Φ)

(-2,(1+2Φ),Φ)

(-2,(1+2Φ),-Φ)

(-2,-(1+2Φ),Φ)

(-2,-(1+2Φ),-Φ)

 

((1+2Φ),Φ,2)

((1+2Φ),Φ,-2)

((1+2Φ),-Φ,2)

((1+2Φ),-Φ,-2)

(-(1+2Φ),Φ,2)

(-(1+2Φ),Φ,-2)

(-(1+2Φ),-Φ,2)

(-(1+2Φ),-Φ,-2)

 

(Φ,2,(1+2Φ))

(Φ,2,-(1+2Φ))

(Φ,-2,(1+2Φ))

(Φ,-2,-(1+2Φ))

(-Φ,2,(1+2Φ))

(-Φ,2,-(1+2Φ))

(-Φ,-2,(1+2Φ))

(-Φ,-2,-(1+2Φ))

 

(1,(2+Φ),2Φ)

(1,(2+Φ),-2Φ)

(1,-(2+Φ),2Φ)

(1,-(2+Φ),-2Φ)

(-1,(2+Φ),2Φ)

(-1,(2+Φ),-2Φ)

(-1,-(2+Φ),2Φ)

(-1,-(2+Φ),-2Φ)

 

((2+Φ),2Φ,1)

((2+Φ),2Φ,-1)

((2+Φ),-2Φ,1)

((2+Φ),-2Φ,-1)

(-(2+Φ),2Φ,1)

(-(2+Φ),2Φ,-1)

(-(2+Φ),-2Φ,1)

(-(2+Φ),-2Φ,-1)

 

(2Φ,1,(2+Φ))

(2Φ,1,-(2+Φ))

(2Φ,-1,(2+Φ))

(2Φ,-1,-(2+Φ))

(-2Φ,1,(2+Φ))

(-2Φ,1,-(2+Φ))

(-2Φ,-1,(2+Φ))

(-2Φ,-1,-(2+Φ))

Thanks to Eric Manning for bringing this insight on bucky ball coordinates to my attention.