Debunking the Debunkers of Golden Ratio Myths.
Overview: This article reviews Dr. George Markowsky’s article on eight misconceptions about the golden ratio. He starts his analysis by establishing a very generous ±2% range for considering evidences of the golden ratio as acceptable. In four cases though, evidences for the original claims are missed or ignored. In two cases, the measurements are taken incorrectly. In two cases, the measurements taken are too limited to be conclusive. In one case, no measurements are taken at all. The arguments are accompanied by weak or incomplete evidence, which is used to dismiss the measurements that vary from the golden ratio by less than 1%. A flawed assumption is made that there are “infinitely numbers near Phi” that could have been used instead. This is of course true in theoretical mathematics, but false with respect to physical measurements in the real world, which are limited by significant figures of accuracy. In addition, the number of reasonable, viable options based on integers, simple fractions, square roots or geometric constructions are far more limited. Here there are less than two dozen likely choices, and the geometric construction of the golden ratio is the simplest of all of them. Many of the conclusions presented are incorrect and incomplete, and new misconceptions are created.
Readers pressed for time: Just read the titles and overviews in bold and view the images shown as supporting evidence.
One of the more commonly referenced articles to “debunk” the golden ratio is “Misconceptions about the Golden Ratio” by Dr. George Markowsky. Dr. Markowsky has a B.S. in Mathematics from Columbia, both a M.A. and Ph.D. in Mathematics from Harvard University and worked in IBM’s research center for ten years. These are very solid credentials indeed. The article’s title, however, is rather unfortunately descriptive of much of its content and conclusions, as you will see in the analysis below.
To be fair, Dr. Markowsky provides accurate information on some common misconceptions about the golden ratio. The article was written before the Internet was widely used, so perhaps some of the information wasn’t as readily available as it is now. To his credit, he actually gathers and analyzes some measurements as evidence, which is far more than can be said of many skeptics and debunkers.
He notes, with the precision of a theoretical mathematician, that “measurements of real objects can only be approximations.” He accordingly proposes a guideline, saying:
I will consider a claim for the golden ratio to be at least reasonable if the computed ratio is within about 2% of Φ.”
He then generously rounds that tolerance up to an “acceptance range” of 1.58 to 1.66. I’m admittedly a golden ratio enthusiast, and that’s a much greater range than I allow for any of my own articles. I usually like to see accuracy to within a pixel or two on high resolution images, or variance of less than 1% from Phi at most. We should be off to a good start.
Dr. Markowsky then adds one other qualification:
Since the acceptance range includes infinitely many numbers near Phi it is necessary to justify that the claim that Phi is the preferred number. Some other ratio coincidentally near Phi might be the important one.”
This sounds reasonable enough on the surface, but this is where the article begins to lose validity. It introduces a flawed assumption that Phi is just like “infinitely many other numbers,” and misses the fact that real world measurements are limited to a small number of significant digits. It also changes the nature of the investigation from one of objective evidence to subjective opinion, deciding what evidence should be included and what constitutes a justification. Many of the “justifications” do not demonstrate a solid investigation and understanding of the claims that are being refuted. As a result, many of his assessments are incomplete and inaccurate.
Let’s review Dr. Markowsky’s analysis of these purported “misconceptions.”
#1. The Name “Golden Ratio” was used in Antiquity
Overview: It is correctly pointed out that the term “golden ratio” didn’t not come about until its use in the 1800’s.
The term to describe the number or ratio 1.618…, what we now usually call the golden ratio, has gone under a variety of different names. Euclid described it as the “extreme and mean ratio.” Renaissance artists of the 1400 and 1500’s knew it as the Divine proportion. It has also been called the golden mean, golden section and golden proportion, and has been represented by the Greek letters phi and tau.
#2. The Great Pyramid was designed to conform to Phi
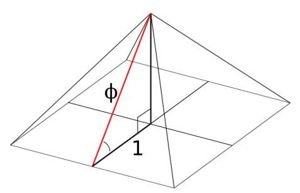
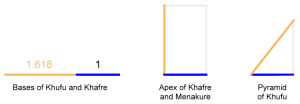
Overview: The Pyramid, completed in 2450 BC, measures to within 0.09% of the golden ratio. This relationship is dismissed though, largely because of ambiguity in the interpretation of a Greek text written about it 2,000 years later in 425 BC. In addition to the golden ratio that appears in the dimensions of the Great Pyramid, golden ratios can also be found in the relative sizes and positions of all three pyramids.
Dr. Markowsky researched the dimensions of the Great Pyramid of Giza and determined that the best available measurements are this:
- The base is 755.79 feet, so the half base of 377.895. (a)
- The height is 481.4 feet. (b)
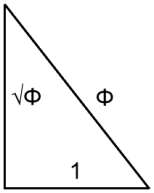
The Pythagorean theorem (a² + b² = c²) reveals the hypotenuse (c) of this triangle to be 612.005 feet. The ratio of the hypotenuse (c) to the height (b) is thus 1.6195.
Eureka! The variance from the golden ratio of 1.618 is only 0.09%. This is a difference of just 7″ in the height of the pyramid from the exact golden ratio.
So can we chalk this one up to a good example of the golden ratio? No, not so fast. Dr. Markowsky references a quote from Herodotus’ History (written about 425 BC) which describes the dimensions of the Great Pyramid. This is followed by a page and a half of narrative discussing the merits of various interpretations of the Greek text. One interpretation reveals a very simple geometry that produces an exact golden ratio relationship – when the area of the face equals the area of the square formed by the height. He concludes, however, that ambiguities in the wording make this interpretation uncertain and summarily dismisses it ALL – despite the FACT the measurements themselves have an astonishingly high degree of accuracy and were well within the acceptance range he just proposed. No other theory is offered to explain its very close correlation to the golden ratio. No other ratio or geometry is offered as a better explanation of its proportions. No rationale is offered as to why a single Greek text written 2,000 years after the pyramid’s construction should establish the validity of the claim.
Dr. Markowsky’s opening premise was that the appearance of Phi has to be justified as the “preferred number” because some other ratio might be the important one, but none is presented. The typical approach in science is to use the best theory available that fits the evidence, not to reject the only reasonable explanation you have without proposing another one. A more scientific approach would be to develop and compare competing theories and then select the one that best explains the known data. The Occam’s Razor principle would require that the simplest of competing theories be preferred to the more complex. As discussed below in this article, golden ratios are easy to create with a variety of simple geometric constructions. One select integer ratio (14/11) is within 0.06% of the height of this Phi-based triangle, and is related to a known method of pyramid construction. This may have been an integer approximation of the golden ratio the Egyptians found in nature, just as the ancients used 22/7 as an approximation of Pi. These approaches provide a much simpler and more rational explanation than the notion that one of the other “infinitely many numbers” available was used.
See my full articles on the Great Pyramid of Giza and on the evidence of the golden ratio in the design of the Giza site. The latter article provides evidence that the use of the golden ratio at Giza is not based on just one isolated instance. The apexes of the pyramids form golden rectangles to within 0.5%, and the bases of Khafre and Khufu are in golden ratio proportion to within 0.3%.
#3. The Greeks used Phi in the Parthenon
Overview: The appearance of the golden ratio in the Parthenon is dismissed because of a single measure that is taken incorrectly from the base of the columns rather than from the base of the steps, which is the traditional approach. Golden ratio relationships in other elements of its construction are ignored.
Dr. Markowsky references nine sources that claim the dimensions of the Parthenon to be based on the golden ratio. He then provides the measurements and presents these dimensions:
- The length is 228′ 1/8″, or 228.0104′ (a)
- The width is 101′ 3.75″, or 101.3125′ (b)
- The height to the base of the triangular apex from the base of the columns (stylobate) is 45′ 1″, or 45.0833′ (c)
- The height to the top of the triangular apex from the base of the columns (stylobate) is 59′ (d)
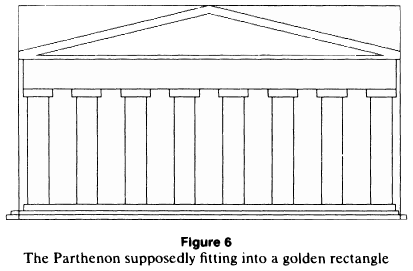
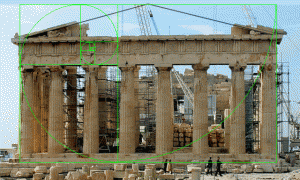
He shows an image (Figure 6) of the Parthenon’s “supposed fit.” For whatever reason, the image has been stretched horizontally to deform it to a ratio of 1.77, and does not represent the Parthenon’s real proportions. This is revealed by an overlay of his image to a photograph of the Parthenon, below center. Note in the image on the right how closely the claimed golden ratio fits the actual structure, with a golden rectangle enclosing the Parthenon, and the two golden ratios (base-column top-apex and column top-beam top-apex) in its height. Click on images for full resolution.
- Markowsky Parthenon illustration
- Markowsky illustration overlayed to actual Parthenon Photo
- Golden rectangle with two golden ratios based on height
He then makes these calculations:
- The ratio of the length (a) to width (b) is 2.25
- The ratio of the width (b) to height (c) is 2.25
- The ratio of the height (b) to width (d) is 1.72
These ratios are all outside his acceptance range. The only one that was even relevant though was the third one (b) to (d), the fit of the face of the Parthenon at its apex within a golden rectangle. He concludes that the claim for use of the golden ratio here is erroneous and proven false. How could all nine of those sources have missed it by so much?
There’s a critical fact that he misses or doesn’t mention. The claims for the appearance of the golden ratio in the Parthenon are not based on just this one measurement. Furthermore, the one measure he does take is from the base of the columns on the floor, while the other claims measure from the steps leading up to the floor. Even his Figure 6 illustration uses the base of the steps, so why is this not used? There is admittedly some room here for interpretation in the proper starting place, but the corrected analysis has a much closer correlation to the golden ratio, as shown in the images above and below. Starting from the second step, we find alignment with the golden ratio, and it’s not just in its overall dimensions fitting inside a golden rectangle. It’s also from the bottom to the top of the columns to the top of the beam, and again from the top of the columns to the top of the beam to the apex of the roof.
These other elements of the building’s design actually provide better evidence yet of its golden ratio relationships, as shown below. None of these examples were addressed in the article, or considered in its conclusion that the golden ratio cannot be found in the Parthenon’s design.
See my full article on the golden ratios in the design of the Parthenon here.
#4. Many painters, including Leonardo da Vinci, used Phi
Overview: Insignificant unfinished works by Leonardo da Vinci are submitted as evidence, along with the lack of any reference to his use of the golden ratio in two biographies written many years later about him. Conclusions are drawn without ever taking a single measurement of the most famous works of any of the artists.
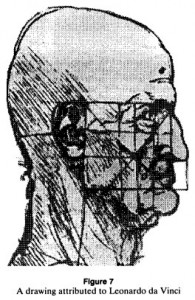
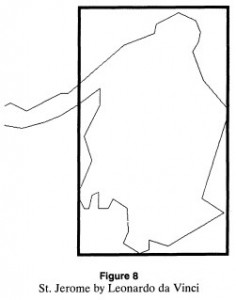
In this instance, Dr. Markowsky quotes claims from various sources and takes no measurements at all. From all of Leonardo da Vinci’s brilliant paintings and illustrations, we’re presented with just these examples as our evidence:
- Human face proportion illustration
- St. Jerome proportion illustration
- Actual image of St. Jerome painting
With these two feable strawmen images now selected for his argument, their shortcomings are presented and the conclusion is drawn that Leonardo did not use the golden ratio in any of his other creations. He also points out that neither of the two biographies on Leonardo da Vinci he reviewed give any mention of Leonardo using the golden ratio.
If some simple measurements of Leonardo’s most famous paintings had been taken, particularly those of religious topics, it would have revealed more than enough evidence to show that Leonardo used this “Divine Proportion” quite extensively and exquisitely in their composition. See the examples below and my full articles on Leonardo’s use of Divine Proportion and his Salvator Mundi. The video below shows dozens of golden ratios incorporated into the exquisite painting “Salvator Mundi.” Furthermore, Leonardo created the illustrations for Luca Pacioli’s book “The Divine Proportion.” The first third of the book is devoted to the importance of the golden ratio in art, so Leonardo would certainly have known of it.
- The Annunciation
- The Last Supper by Leonardo da Vinci
It was said that artist Georges Seurat “attacked every painting with the golden ratio.” Dr. Markowsky summarily dismisses Seurat’s use of the golden ratio without taking a single measure of Seurat’s hundred plus paintings and illustrations. He simply references one study that found “no justification” for the golden ratio lines drawn by someone on Seurat’s paintings, and another study whose author was unable to find any golden ratios at all. These findings are surprising, because it’s not that difficult to find clear examples. Seurat’s use of the golden ratio are shown below.
- Seurat painting with golden ratios at horizon, pier and sail
- White lines – horizontal golden ratios. Red lines – vertical.
- Golden ratio at horizon, knees and ankles
- Sail boat within golden ratios
- Horizon and smoke stack at golden ratios
In addition, Seurat created two dozen or more paintings on small wood panels that were cut to golden rectangle proportions, as illustrated below:
See my article on Seurat’s use of the golden ratio, which shows many more examples.
The use of the golden ratio by Botticelli, Raphael, Michelangelo, Dali or others is never explored. He simply concludes this topic with one final sentence referencing someone else’s study of “the alleged use of the golden ratio by other painters, including Le Corbusier.”
Ironically, Le Corbusier is best known as an architect. Among his most prominent projects is the UN Secretariat Building, which brings us to #5.
#5. The UN Building embodies the Ratio Phi
Overview: The ratio is simplistically and incorrectly calculated using the wrong dimensions of the building. The correct measures are within 0.9% of the golden ratio. No awareness is shown that the building’s lead architect was a pioneer and advocate of the golden ratio in design.
Dr. Markowsky called the UN and received these measurements for the UN Secretariat Building:
- Height of 505′ (with heights at other elevations of 544′ and 550′)
- Width of 287′
- Depth of 72′
He then very simplistically divided 505 by 287 to get a ratio of 1.76. He tried again with 544′ and 550′ and calculated ratios of 1.90 and 1.92. He saw that these ratios were outside his acceptance range, aborted any efforts to understand the claims and concluded “the Secretariat building does not appear to be designed on the basis of the golden ratio.” He also consulted “several architecture books” and could not find the golden ratio in their indexes. End of story. Another myth debunked.
Here’s what was missed:
- The design is based on three stacked golden rectangles – Anyone who’s ever seen the very popular 1959 Disney classic educational short “Donald in Mathmagic Land” is likely to know this: The design of the UN Building is based on three golden rectangles stacked on their sides, not its simple height and width. This Academy Award-nominated movie has been shown in math classes for decades. Dr. Markowsky even acknowledges his familiarity with this work in a book review he later wrote. The three stacked golden rectangles result in the following relationships:
- Divide the width of 287 by 1.618 to get 177.38 feet as the rectangle’s side.
- Multiply 177.38 by 3 to get the height of the three stacked rectangles at 532′.
- Take the elevations of 505′ and 550′ to get an average of 527.5′.
- The golden rectangle-based height of 532 is only 0.9% greater than the average height of 527.5′, which is well within Dr. Markowksy’s “acceptance range.”
- The building’s architect was a golden ratio advocate – Le Corbusier, one of the building’s lead architects was passionate about the golden ratio in design.
- He developed a golden-ratio based design system called “Le Modulor” in 1943.
- He presented it in the United States in 1946.
- He led the architectural design project for the UN Secretariat building, which was constructed in 1947 through 1952.
- The evidence is easily measured – Image analysis of the UN Secretariat Building shows that it embodies many golden ratios in its design.
- Design with 3 stacked golden rectangles
- UN Secretariat Building dividing lines based on golden ratios
- UN Secretariat window configuration reveal golden proportions
See my full article on the UN Secretariat Building’s design.
#6. A Golden Rectangle is the Most Aesthetically Pleasing Rectangle
Overview: A survey from 1860 of people’s “favorite rectangle” showed a preference for the golden ratio, and the ratios closest to it. The survey is recognized as having questionable relevance and lacks context. Dr. Markowsky expands the selection to 48 choices, making the selection more difficult and less relevant yet. Data gathered from surveys he conducted with this 48 choice version is used this to conclude that a preference for the golden ratio is false. A more relevant survey would be to test this with images that have context, such as a human face.
Dr. Markowsky references five articles/books which discuss studies that show that people prefer a golden rectangle to rectangles with other dimensions. He notes that most of these are based on the original research in the 1860’s by Gustav Fechner that had study participants choose from 10 rectangles. Rectangles with ratios of 0.57, 0.62 and 0.67 (i.e. approximating the golden ratio of 0.618) were chosen 76% of the time. Dr. Markowsky expanded this test to include 48 rectangles, which obviously makes it hard to even distinguish a golden rectangle from all the others. Is there any science to suggest that this plethora of choices makes the test more accurate or meaningful? Would the test be better yet with 100 rectangles from which to choose? He concluded that people prefer rectangles in a certain range, but found no evidence to show people specifically preferred a golden rectangle.
- Fechner’s 10 rectangles – Select your favorite
- Markowsky’s 48 rectangles – Select your favorite (Good luck!)
- The 48 rectangles by size. Imperceptible variations.
This is an interesting study, but I have to question its validity. Others do as well, including Gustav Fechner who developed it. It shows a collection of rectangles with no context. Asking people to select a favorite rectangle from a group of random rectangles is a bit like playing dozens of musical notes and asking them to select their favorite. Musical notes only have context in relation to music created. Golden ratios only have context in relation to aesthetics of the creations in which they appear.
People have favorites of many things, but have you ever heard anyone talk about their favorite rectangle? For what? For a dinner plate? A memo pad? A desktop? An eraser? Wouldn’t anyone’s “favorite” rectangle depend on its context and purpose?

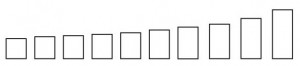
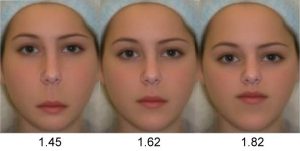
The human head often has near golden ratio proportions in its height to width. To test if the golden ratio is intrinsically related to aesthetics and beauty, a much more relevant and meaningful question would have been this: “Which of the following facial images do you find most attractive?”
Which one do you think most people would select as the most attractive rectangle, now that there is some context to the question?
The rectangles of the heads (from hair top to chin, and where the inner upper ears meet the head) have the following ratios:
2.59, 2.30, 2.06, 1.80, 1.62, 1.40, 1.26, 1.11
The fifth head from the left has golden rectangle proportions.
The appearance of the golden ratio in nature and the arts is generally based on a dividing point of a line or dimension into two parts, not by forming a rectangle. As another example, which ratio below results in the most attractive position of the mouth in relation to the eyes and chin?
This brings us to #7.
#7. The Human Body Exhibits Phi
Overview: Dr. Markowsky’s own family members average to within 0.7% of the golden ratio on the measure of their navel to their height. The relationship to the golden ratio is then dismissed because of general uncertainties as to exactly where to take the measurements, and the fact that a book he reviews uses too many significant decimal places (1.61803) in their examples of the golden ratio in two old statues and several animals. Other appearances of the golden ratio in the human form and facial features are ignored.
Dr. Markowsky knew that the navel is often said to be positioned at a golden ratio of one’s height. He took measurements of his own family members and found all their measures to be within his “acceptance range.” The average was 1.63, which is only a 0.7% variance from the golden ratio. Eureka! This claim must be true, right? Not so fast.
He raises an objection about the “precise location of the navel” rather than simply using its midpoint. A ±2% variance on a 5’6″ person gives us 2.64″ range in which to find a valid golden ratio measuring point with Dr. Markowsky’s “acceptance range.” It would be a rare person with a navel anywhere near that large. He then proceeds to discuss unseen sketches of two Greek statues with missing body parts as his evidence. His main objection is that some body parts do not offer just a single measurement point, and that the proportions in the book he reviewed cannot be accurate to the five significant decimal places of Phi, as was referenced by the authors. What happened to the “acceptance range?” Next he makes reference to some unseen images of golden ratios in animals and there takes objection again to the author’s reference to 1.61803 because of it’s excessive significant decimal places of accuracy. He ignores his own body measurement experiment that was within the “acceptance range” and dismisses the concept of the golden ratio in the human body entirely.
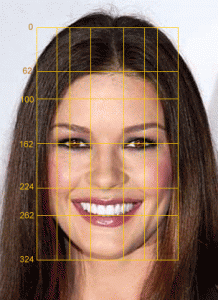
Dr. Markowsky never mentions, let alone measures, the perhaps most interesting appearances of the golden ratio in living creatures. These are found in the human face, and impact our perceptions of beauty.
- Animation of common golden ratios
- Facial golden ratios, vertical and horizontal
- Golden ratio facial analysis
See my series of articles on the golden ratio and beauty.
#8. Virgil’s Aeneid Exhibits Phi
Overview: Dr. Markowsky references a claim by one person that Virgil’s Aeneid is based on Phi. This straw man claim is rarely used as a good example of the golden ratio, so it doesn’t merit trying to prove or disprove it.
This claim is based on the assertion by one person, Professor George Eckel Duckworth, that Virgil used Phi as a key element in this writing. Maybe, or maybe not, but the example is so arcane that it is rarely offered as a great example of the golden ratio. It hardly belongs in any overall assessment of the validity of the golden ratio’s appearances or applications. In my fifteen plus years of running GoldenNumber.net, the only people I’ve ever heard make reference to this claimed application are the debunkers who are looking for a quick and easy win. Let’s let them have this one.
Recap of the “Misconceptions” about the Golden Ratio.
Dr. Markowsky presents what looks to be an objective, scholarly attempt to investigate and correct various misconceptions about the golden ratio. There are only eight examples given, and in my analysis we find:
- Four cases in which evidences for the original claims are missed or ignored (Parthenon, UN Secretariat Building, famous artists, human body)
- Two cases in which the measurements were taken incorrectly. (Parthenon, UN Secretariat Building)
- Two cases in which the measurements taken were far too limited to be conclusive. (Parthenon, human body)
- One case in which no measurements were taken at all. (Famous artists)
- Five cases in which actual results are far better than his acceptance range, but were dismissed due to subjective reasoning, inadequate evidence or misunderstanding of the basis of the original claim. (Great Pyramid, Parthenon, famous artists, UN Secretariat Building, human body)
- Two cases in which the claim examined was not viewed by most informed people as a meaningful or significant claim anyway. (Favorite rectangles, Virgil’s Aeneid)
You can decide whether this meets your own “acceptance range” for an objective, credible academic analysis of appearances and applications of the golden ratio.
Flawed assumptions can lead to flawed conclusions
In addition to the above errors in method, there is an critical flaw in Dr. Markowsky’s opening statement:
Since the acceptance range includes infinitely many numbers near Phi it is necessary to justify that the claim that Phi is the preferred number. Some other ratio coincidentally near Phi might be the important one.”
With this assumption, he turns his investigation into one of looking for a needle in an infinitely large haystack. The odds of finding anything that fits the golden ratio exactly, with its infinite number of decimal places, become infinitely small. This is not the case in the real world, where we routinely use meaningful, discernible, finite physical measurements. That’s why your ruler only has a limited number of dividing lines. There are physical and engineering limitations on our ability to build something with much more than four or five decimal places of accuracy, and there is often any no need for any more precision. When you’re measuring the Great Pyramid, getting a golden ratio to within mere inches of its 481.4′ height (5776 inches) should be close enough to come to a reasonable conclusion that it might well have been a factor in its design. It only takes four significant decimal places to do that, not an infinite number. There are only 33 numbers with four significant decimal places that have a variance from Phi of less than 1%, not “infinitely many numbers.” These range in increments of 0.001 from 1.602 to 1.634, so those are really the only relevant ratios to use. As, I’ll illustrate below, there are only a handful of integer relationships and triangles that produce a result this close to phi. If phi is not the likely or “preferred” number, then wouldn’t a scientific approach require that one propose a better or competing theory rather than simply dismissing the best available explanation?
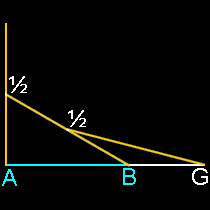
Many basic geometric constructions create golden ratio proportions
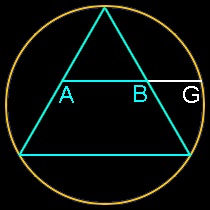
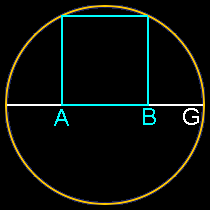
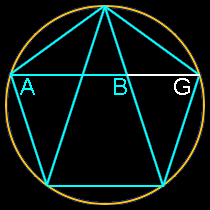
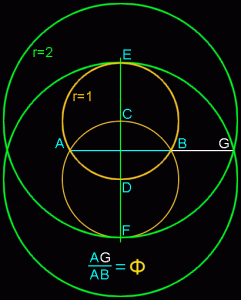
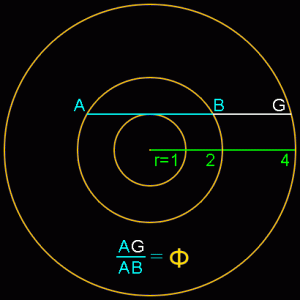
It’s also unreasonable to assume that any artist or architect would set out to base a proportion on number that was very, very close to phi, but decidedly not phi. Would the ancient Egyptians, Greeks or even a genius like Leonardo da Vinci set out to create a work of art based on some number close to Phi but not Phi, such as 1.618123456789? The exercise would be meaningless because no one could achieve that level of precision. Any proportion these artists would have used would likely be the result of some integer ratio, say 8/5, or the result of a simple geometric construction. Golden ratios are rather easy to find and create in geometry, even if you’re not trying. Look at all these relatively simple constructions which all produce golden ratios (AG/AB):
 |
 |
Note how this section of the Parthenon below mirrors the two most basic golden ratio constructions above. These are formed by simply swinging an arc on a rectangle with one side twice as long as its other side. There’s simply no need here for complicated ratios or theoretical mathematics with infinite possibilities.

Parthenon: Alternative ratios of design
In practice, it’s frankly much easier and more feasible to incorporate a golden ratio in a design and be off by a very small margin in the execution, than it is to find some other ratio close to Phi and hit it with exacting precision. Can anyone show a single simple geometric construction that produces a proportion close to Phi, but not Phi? I’ve not seen one so what else would these designers and architects have been using?
See also my articles on Phi and Geometry.
Very few opportunities exist to construct ratios that are near the Golden Ratio
There may be infinitely many numbers near Phi, but precious few that can be created by simple integer ratios. Consider this:
- Only 10 ratios near Phi – If you take all possible ratios of the integer numbers from 1 to 50, there are 1275 that are greater than or equal to one. Only 10 of these result in a unique ratio with a variance from Phi of less than 1%.
| Ratio | Decimal | Variance |
| 13/8 | 1.625 | 0.43% |
| 21/13 | 1.615 | -0.16% |
| 29/18 | 1.611 | -0.43% |
| 31/19 | 1.632 | 0.84% |
| 34/21 | 1.619 | 0.06% |
| 37/23 | 1.609 | -0.58% |
| 44/27 | 1.630 | 0.72% |
| 45/28 | 1.607 | -0.67% |
| 47/29 | 1.621 | 0.16% |
| 49/30 | 1.633 | 0.95% |
Note: 13/8 can also be expressed as 26/16 and 39/24. 21/13 can also be expressed as 42/26. Fibonacci sequence numbers are in bold.
- Only 5 right triangles near Phi – If you take all the possible right triangles based on integer numbers of 1 to 50 for two sides or the hypotenuse, there are also 2550 unique combinations. Only 5 of the resulting triangles are like the Great Pyramid. with a variance of less than 1% from Phi.
| Side A (1) | Side B (√Φ) | Hypotenuse C (Φ) | Variance |
| 8.660 | 11 | 14 | -0.09% |
| 11 | 14 | 17.804 | +.02% |
| 26 | 33 | 42.012 | -.08% |
| 28.983 | 37 | 47 | +.22% |
| 37 | 47 | 59.816 | -.05% |
Note: 8.660 – 11 – 14 can also be expressed as its multiples of 17.321 – 22 – 28 and 25.981 – 33 – 42.
The 11 x 14 triangle can also be expressed as its multiples of 22 x 28 and 33 x 42.
Curiously, one theory for the dimensions of the Great Pyramid proposes it is based on a triangle with a hypotenuse and side of 7 and 5.5. This is the same ratio as the 14 and 11 triangle above. If this is the case, we then have to ask why they chose these numbers, other than as an amazingly accurate rational representation of Phi.
The Golden Ratio is infinitely more probable to appear than “infinitely many other numbers”
Overview: Despite the “infinitely many numbers” near Phi, there are only less than 20 ratios that can be created with integers less than 50. Phi is the most likely choice when compared to all the other close alternatives.
So in reality, that “infinitely many numbers,” or ratios, that artists and architects have to choose from in creating something that looks like Phi, but isn’t Phi, is probably less than 20. Take a good look at the lists above and see if any of the numbers involved strike you as likely candidates, numbers that have some special significance on their own that would have made them more worthy of selection than Phi itself.
Another problem with the “infinitely many numbers” premise is that Phi is not just another number among an infinite set of others, or even among the 20 sets of numbers that get you close to it. To the contrary, Phi is one of the most unique numbers in mathematics, geometry and life, with properties that no other number has. It can be derived mathematically through a variety of limits. It appears in dozens of geometric constructions. It’s found in spiral growth patterns in nature. It’s found in the world of quantum physics, crystals and DNA molecules. It’s found in the relative dimensions of the moon and Earth and beyond. Even without knowledge of all that, it’s often found in the proportions of a beautiful face, or perhaps in the proportion of one’s own navel to their height. It’s a very unique and very ubiquitous ratio, and it’s innately familiar to us. It’s properties create efficiency in design, as well as visual harmony and beauty like no other number. It’s been recognized by mankind since the time of the ancients for its relationship to nature and its value in aesthetics.
So when you think about it that way, when we see something that is less than a percent away from Phi, the likelihood that an artist or architect used Phi instead of these close substitutes is really quite high. Even if they did chose another, we’d have to ask what made them select a proportion so very close to Phi rather than an entirely different proportion altogether (e.g., 1.414 as the square root of two, 1.5, 1.732 as the square root of three, 2, etc.).
A Sherlock Holmes view of the evidence
Phi appears extensively in mathematics and geometry. The universe is based on mathematics and geometry. Look to the evidence and reason in determining if Phi is at present. As with a good detective novel, we find the means, the motive and the opportunity.
Dr. Markowsky says that it’s “necessary to justify that the claim that Phi is the preferred number,” but in reality there aren’t that many options that make any more sense than Phi. No other options are are even offered in his analysis. We can’t get a signed affidavit from the ancient Egyptians and Greeks, Leonardo da Vinci, Georges Seurat, Mother Nature or God Himself to verify that Phi was in fact used. Nor should we expect the answers to be found in books written 2,000 years after the Great Pyramid was built, or biographies written hundreds of years after Leonardo lived, in order to see and understand intent in design with reasonable certainty. We must make the most reasonable assumptions possible given the evidence available. Le Corbusier presented his golden ratio-based design system, Le Modulor, just years before he lead the design of the UN Secretariat Building, but that didn’t qualify as justification either.
Phi appears extensively throughout mathematics and geometry. The physical universe is based on mathematics. What basis in reason is there to then suspect that an infinite number of other very close ratios with no particular significance in mathematics and geometry would then express themselves in the simple, fundamental patterns in the universe?
Has mankind also applied this ratio in its own creations? We need to look at the evidence itself and apply reason. As with any detective novel, we just need to ask if there was the means, motive, and opportunity. The means can be as simple as a marker and a piece of string. The motive can be simply to appreciate and recreate the beauty and harmony of all we see in the world around us, consciously or not. The opportunities to create with Phi are then “infinitely many.”
I invite your commentary and will correct anything in the article that is not accurate or fairly presented. Post your thoughts below.
Note on images used for illustration and evidence
All illustrations with overlaying grids in this article were created with PhiMatrix, which is accurate to within a pixel. Each line shown is in golden ratio proportion to the ones of either side of it. PhiMatrix is available for with a two week free trial through this link. Do your own tests, gather your own evidence and come to your own conclusions.
Quotations
“The good, of course, is always beautiful, and the beautiful never lacks proportion.”
–Plato
“Measure what is measurable, and make measurable what is not so.”
–Galilei, Galileo (1564 – 1642), Quoted in H. Weyl “Mathematics and the Laws of Nature” in I Gordon and S. Sorkin (eds.) The Armchair Science Reader, New York: Simon and Schuster, 1959.
“[The universe] cannot be read until we have learnt the language and become familiar with the characters in which it is written. It is written in mathematical language, and the letters are triangles, circles and other geometrical figures, without which means it is humanly impossible to comprehend a single word.”
–Galilei, Galileo (1564 – 1642), Opere Il Saggiatore p. 171.
“Where there is matter, there is geometry.”
–Kepler, Johannes (1571-1630), (Ubi materia, ibi geometria.) J. Koenderink Solid Shape, Cambridge Mass.: MIT Press, 1990
“The human mind has first to construct forms, independently, before we can find them in things.”
–Einstein, Albert (1879-1955)
“Nature hides her secrets because of her essential loftiness, but not by means of ruse.”
–Einstein, Albert (1879-1955)
References
Dr. George Markowsky – Misconceptions about the Golden Ratio – MAA article (Also at Markowsky site)
Google Shortcode for this Article: http://goo.gl/EGS1kI












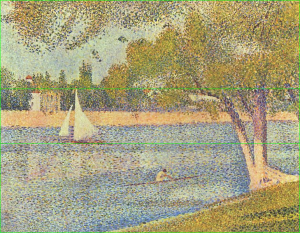
















I agree, setting a Phi-0.618 structure to a graphic composition (drawing, painting, plan, etc.) is like defining the rhythm on a musical partiture; it is a guideline for interpretation and perception. Measuring deviations on the interpreted piece to try to debunk the existence of a rhythmical intention, is, to be polite, not serious,
Hello, This article is awesome and I applaud and praise you for it, but not trying to be malicious or negative about this comment I think you have a mistake in your calculations of the ratio of the hypotenuse to the height in your pyramid portion of your article. If the height is 481.4 and the Hypotenuse is 612.005 then shouldn’t the answer be 1.2713? I have checked it with several calculators and my laptop. Sorry.
JMM
Thank you Juan for the supportive words. You’re correct that the ratio of hypotenuse of 612.005 to the height of 481.4 is 1.2713. That is not the measure in question though. A perfect phi-based triangle has these proportions:
Base – 1
Height – Square root of Phi = 1.27201965…
Hypotenuse – Phi = 1.61803399…
So the ratio of the hypotenuse to the height AND the height to the base are both 1.27201965, the square root of two. In the Giza pyramid the ratio of the hypotenuse to the height is 1.27130 and the height to the base is 1.27390.
The variance of the Giza pyramid to the Phi pyramid is 1.27130/1.27201965 or 1.27390/1.27201965, a variance of 0.1% in both ratios. The hypotenuse of the Giza pyramid is 1.61951173 times the base, while the hypotenuse of the Phi pyramid is 1.6180339887 of it’s base. This is a variance of only 0.09%.
Interesting article.
Please refer to relevant work:
http://www.stefanides.gr/pdf/2012_Oct/PHOTO_12.pdf
http://www.stefanides.gr/pdf/2012_Oct/PHOTO_13_GEOMETRY_DESIGN.pdf
Regards from Athens,
Panagiotis Stefanides
Well said, Gary. Your wonderful software, Phi Matrix, has been a very useful and revealing tool in my photography. Not only does it help when cropping for a more pleasing composition, but it also shows how I am naturally drawn to the proportion even before cropping. Using Phi Matrix to analyse the work of others shows that either we all know about and use the golden ratio without saying it, or there actually IS a natural proclivity we all share.
I don’t like the role of devil’s advocate, but some points of your argumentation against Markowsky need some light.
– The so-called Herodotus’ quote (the area of a face of Kheops equals the area of the square formed by the height) is a fake, that has nothing to do with the original Herodotus, and this is well-known today.
– Still about Kheops, it’s quite easy to admit the architects used a ‘seked’ of 5.5, without thinking of the golden ratio, unknown from ancient Egypt, as far as we know.
– About the Parthenon, it is now known that the main ratio used was 16/9 ths.
– About all artworks allegedly based on Phi, the accuracy of measurements never proves anything, as far as the author does not give his purpose.
I quite appreciate the findings of Gary and others, and I’m myself a Phi addict, but my own experience shew me incredible coincidences happen around the Phi phinomena.
My poor English doesn’t allow me to give a full account of it, but I tried to translate some of my stuff:
http://quaternity4.blogspot.com/2016/03/46665.html
http://quaternity4.blogspot.com/2012/10/dne-ratio.html
http://perecqation.blogspot.com/2017/03/sixteen-tones.html
Thanks for your comments, Remi. A few responses:
The disturbing thing to me about the Herodotus quote is that the validity of the quote was used to dismiss statements about the pyramids rather than the actual measurements of the pyramids.
It will could be that the 5.5 seked was used, but the question is then WHY that ratio rather than some other, especially when it is about as mathematically as close as you can get using integer numbers to the actual golden ratio.
The Parthenon is known to use many numbers and ratios, not just 16/9, and my measurements of high resolution images in my article at https://www.goldennumber.net/parthenon-phi-golden-ratio/ show proportions of design that are very closely aligned to Phi (1.618…), and nowhere near 16/9 (1.777…)
Measurements on artwork cannot “prove” that the golden ratio was applied by the artist, at least not without a written testimony by the artist, but repeated applications of the the golden ratio within a composition with as much accuracy as can be achieved is certainly very strong and compelling evidence. And given the evidence, one has to ask why it is logical or reasonable to assume that the artist did not apply the golden ratio. It’s been known about since the time of the ancients, and was covered explicitly by Euclid in a number of his constructions in Elements, a book that one of the most translated and distributed in all of history. It was THE geometry book from which all students learned until other texts on the subject began to be written only in the past couple of centuries.
Great article, great find. Thank you for such rigid golden clarity.
If you’re not familiar with this man’s work, I think you’ll find it interesting or at least remarkable. Kind of represents the absolute opposite of what Markowsky tried to do by acidifying the omnipresence of a sublime principle by his sour soul.
https://www.youtube.com/watch?v=6DleAx-bxIs&t=3s
and a more in depth presentation:
https://www.youtube.com/watch?v=upzjM7-83LE
Thanks, a true joy to read
Markowsky claiming that the Golden Ratio was not used in the many paintings of the Renaissance is definitely cynical. I suspect that the use of golden calipers was the artist’s secret weapon at the time, and was a long-lived fad.
I would suspect that a craftsman could easily build golden calipers with the technology of the time, allowing the artist to completely bypass a compass and straightedge construction,
Considering that learned artists would have studied Euclid’s Elements, the premiere GEOMETRY textbook that was required study at most European universities up until the 20th century, it seems inconceivable that they would have all ignored Book VI Def. 3 and the many other constructions of the Extreme and Mean Ratio when searching for inspiration.
Your comments are spot on:
– Euclid’s Elements was THE geometry textbook for centuries after it was written in about 300 BC, only being replaced by other geometry textbooks in modern times.
– Elements has at least 10 propositions that describe the cut of extreme and mean ratio, aka the golden ratio.
– The divider has been a common tool of artists and artisans since antiquity for measurements and proportions.
– All it takes to create a golden ratio caliper is to join the two arms of a divider at the golden ratio cut described in Euclid’s Elements. No “construction” with compass and straight edge is needed, except once for the purpose of constructing the golden caliper.
It does seem inconceivable that best artisans working on the most important projects of their culture would not have realized and used this, especially when the evidence exists in so many works that it was known and applied with intent and accuracy.