The Great Pyramid of Egypt closely embodies Golden Ratio proportions.
There is debate as to the geometry used in the design of the Great Pyramid of Giza in Egypt. Built around 2560 BC, its once flat, smooth outer shell is gone and all that remains is the roughly-shaped inner core, so it is difficult to know with absolute certainty. The outer shell remains though at the cone, so this does help to establish the original dimensions.
There is evidence, however, that the design of the pyramid may embody these foundations of mathematics and geometry:
- Phi, the Golden Ratio that appears throughout nature.
- Pi, the circumference of a circle in relation to its diameter.
- The Pythagorean Theorem – Credited by tradition to mathematician Pythagoras (about 570 – 495 BC), which can be expressed as a² + b² = c².
So how might the Great Pyramid have embodied these concepts? There are a number of theories to explore.
Update: See also the article on golden ratios in the site design of the Giza Pyramid complex.
A pyramid based on Phi varies by only 0.025% from the Great Pyramid’s estimated dimensions
Phi is the only number which has the mathematical property of its square being one more than itself:
Φ + 1 = Φ²
or
1.618… + 1 = 2.618…
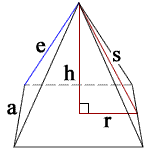
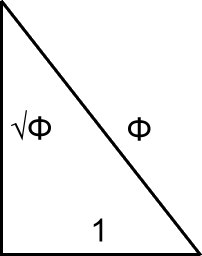
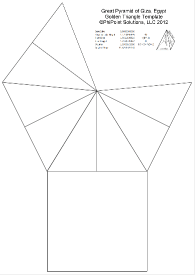
By applying the above Pythagorean equation to this, we can construct a right triangle, of sides a, b and c, or in this case a Golden Triangle of sides √Φ, 1 and Φ, which looks like this:
This creates a pyramid with a base width of 2 (i.e., two triangles above placed back-to-back) and a height of the square root of Phi, 1.272. The ratio of the height to the base is 0.636.
According to Wikipedia, the Great Pyramid has a base of 230.4 meters (755.9 feet) and an estimated original height of 146.5 meters (480.6 feet). This also creates a height to base ratio of 0.636, which indicates it is indeed a Golden Triangles, at least to within three significant decimal places of accuracy. If the base is indeed exactly 230.4 meters then a perfect golden ratio would have a height of 146.5367. This varies from the estimated actual dimensions of the Great Pyramid by only 0.0367 meters (1.4 inches) or 0.025%, which could be just a measurement or rounding difference.
A pyramid based on golden triangle would have other interesting properties. The surface area of the four sides would be a golden ratio of the surface area of the base. The area of each trianglular side is the base x height / 2, or 2 x Φ/2 or Φ. The surface area of the base is 2 x 2, or 4. So four sides is 4 x Φ / 4, or Φ for the ratio of sides to base.
A pyramid based on Pi varies by only 0.1% from the Great Pyramid’s estimated dimensions
There is another interesting aspect of this pyramid. Construct a circle with a circumference of 8, the same as the perimeter of this pyramid with its base width of 2. Then fold the arc of the semi-circle at a right angle, as illustrated below in “Revelation of the Pyramids”. The height of the semi-circle will be the radius of the circle, which is 8/pi/2 or 1.273.
This is only 1/10th of a percent different than the height of 1.272 computed above using the Golden Triangle. Applying this to the 146.5 meter height of the pyramid would result in a difference in height between the two methods of only 0.14 meters (5.5 inches).
A pyramid based on areas is identical in geometry to one based on Phi
In addition to the relationships of the pyramid’s geometry to phi and pi, it’s also possible that the pyramid was constructed using a completely different approach that simply produced the phi relationship. The writings of Herodotus make a vague and debated reference to a relationship between the area of the surface of the face of the pyramid to that of the area of a square formed by its height. If that’s the case, this is expressed as follows:
Area of the Face = Area of the Square formed by the Height (h)
(2r × s) / 2 = h²
We also know by the Pythagorean Theorem that r² + h² = s² , which is equal to s² – r² = h², so
r × s = s² – r²
Let the base r equal 1 to express the other dimensions in relation to it:
s = s² – 1
Solve for zero:
s² – s – 1 = 0
Using the quadratic formula, the only positive solution is where s = Phi, 1.618…..
This same relationship is shown on the Mathematics of Phi article, where we how Phi is calculated based on dividing a line so that the ratio of the line to the larger section is the same as the ratio of the larger section to the smaller section. If the height area to side area was the basis for the dimensions of the Great Pyramid, it would be in a perfect Phi relationship, whether or not that was intended by its designers. If so, it would demonstrate another of the many geometric constructions which embody Phi.
A pyramid based on a constant gradient varies by 0.8% from the Great Pyramid’s estimated dimensions
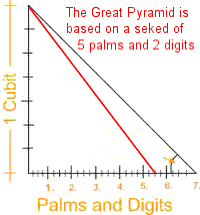
Yet another possibility is that the Great Pyramid is based on another method, known as the seked. The seked is a measure of slope or gradient. It is based on the Egyptian system of measure in which 1 cubit = 7 palms and 1 palm = 4 digits. The theory is that the Great Pyramid is based on the application of a gradient of 5.5 sekeds. This measure means that for a pyramid height of 1 cubit, which is 7 palms, its base would be 5.5 palms. The ratio of height to base then is 7 divided by 5.5, which is 1.2727. This is very close to the square root of Phi, which is 1.27202. The slope of a pyramid created with sekeds would be 51.84°, while that of a pyramid based on phi is 51.83°. The seked method was known to be used for the construction of some pyramids, but not all. If used on the Great Pyramid it should have resulted in a height of 146.618 meters on a base of 230.4 meters. This is 0.118 meters (4.7 inches) greater than the actual estimated height of the Great Pyramid. This variance of 0.8% thus does not match the geometry of the Great Pyramid as closely as the geometries based on phi or pi. This result is very close to the dimensions of the Great Pyramid. The question remains though as to why 5.5 would be chosen over some other number for the gradient. What was more appealing about 5.5 rather than simply using a gradient based on 5 or 6? Even without a mathematical knowledge of Phi, a simple awareness of the golden ratio observed in nature might have led choosing this proportion.
Illustration of the Seked method (Image credit to David Furlong):
Its near perfect alignment to due north shows that little was left to chance
One thing that is clear is that the dimensions and geometries were did not happen by chance. Would a civilization with the technological skill and knowledge to align the pyramid to within 1/15th of a degree to true north leave the dimensions of the pyramid to chance? If they did not intend the geometry that resulted in a rather precise angle like 51.83 degrees, why would they have not used another simpler angle found in divisions of a circle such as 30, 45, 54 or 60 degrees? Only one other Egyptian pyramid used this geometry or angle of incline, the Meidum pyramid, and it’s a step pyramid with three tiers. Given that there are several ways based in simple geometry by which the Great Pyramid could have ended up with this precise angle, it seems unreasonable to suggest that none of them apply, until another equally plausible and accurate theory can be presented.
Other possibilities for Phi and Pi relationships
If the Egyptians were using numbers that they understood to be the circumference of the circle to its diameter or the golden ratio that appeared in nature, it’s difficult to assume that they truly understood the actual decimal representations of pi and phi as we understand them now. Since references to phi don’t appear in the historical record until the time of the Greeks hundreds of years later, some contend that the Egyptians did not have this knowledge and instead used integer approximations that achieved the same relationships and results in the design.
A rather amazing mathematical fact is that pi and the square root of phi can be approximated with a high degree of accuracy using simple integers. Pi can be approximated as 22/7, resulting in a repeating decimal number 3.142857142857… which is different from Pi by only 4/100’s of a percent. The square root of Phi can be approximately by 14/11, resulting in a repeating decimal number 1.2727…, which is different from Phi by less than 6/100’s of a percent. That means that Phi can be approximated as 196/121.
The Great Pyramid could thus have been based on 22/7 or 14/11, which is the same as 7/5.5, in the geometries shown above. Even if the Egyptians only understood pi and/or phi through their integer approximations, the fact that the pyramid uses them shows that there was likely some understanding and intent of their mathematical importance in their application. It’s possible though that the pyramid dimensions could have been intended to represent only one of these numbers, either pi or phi, and the mathematics would have included the other automatically.
We really don’t know with certainty how the pyramid was designed as this knowledge could have existed and then been lost. The builders of such incredible architecture may have had far greater knowledge and sophistication than we may know, and it’s possible that pi , phi or both, as we understand them today, could have been the factors in the design of the pyramid. It could be that they chose other approaches that resulted in almost identical geometries.
A detail of the geomatries and calculations is below:
| Pyramid | Base in Meters | Height in Meters | Base/2 in Meters | Ratio of Height / (Base/2) | Angle Radians using (ATAN) | Convert Angle to Degrees | Variance from Actual in Meters | % Variance from Actual |
| Great Pyramid of Giza | 230.4 | 146.50000 | 115.20 | 1.271701 | 0.90443531 | 51.82033 | ||
| Phi Geometry | 2.0 | 1.27202 | 1.00 | 1.272020 | 0.90455689 | 51.82729 | ||
| Phi to Scale | 230.4 | 146.53666 | 115.20 | 1.272020 | 0.90455689 | 51.82729 | 0.0367 | 0.025% |
| Pi Geometry (8/pi/2) | 2.0 | 1.27324 | 1.00 | 1.273240 | 0.90502258 | 51.85397 | ||
| Pi to Scale | 230.4 | 146.67720 | 115.20 | 1.273240 | 0.90502258 | 51.85397 | 0.1772 | 0.121% |
| 5.5 Seked | 230.4 | 146.61818 | 115.20 | 1.272727 | 0.90482709 | 51.84277 | 0.1182 | 0.081% |
One fact and one interesting question remains
The fact is that whatever method was used in its design, the end result represents the geometry of a phi-based triangle with a high degree of accuracy.
The interesting question is “why did they choose this specific shape geometry and configuration of three pyramids for the Great Pyramid?” It’s different than the rest and was clearly done with intent. Was it because it appeared more beautiful, more aligned with nature? If not that, what other reasons did they have that captured this one number associated with nature and beauty?
Construct your own pyramid to the same proportions as the Great Pyramid
Use the template below in gif or pdf format:
Thanks go to Jacques Grimault for these insights, and for other fascinating facts and speculations presented about ancient pyramids in the movie on “The Revelations of the Pyramids.”
References:
http://en.wikipedia.org/wiki/Great_Pyramid_of_Giza
http://en.wikipedia.org/wiki/Ancient_Egyptian_units_of_measurement
http://www.kch42.dial.pipex.com/sekes0.htm
http://earthmatrix.com/great/pyramid.htm
Great Pyramid Giza Site Complex Golden Ratios
The base of the great pyramid could be equal to b=c/π/(sqrt(2)-1) which is in my calculations somewhere close to 230.380924 meters using:
b=base, c=lightspeed (current best estimate) = 299792458 m/s, π=3.141592653589793238462643383279 (some “signigficant” number of decimals:-),
sqrt(2)-1=0.414213562 which also happens to be a nice number since 1/(sqrt(2)-1)=2.414213562 (which is exactly 2 higher)
also,
If you do some calculations on the height it turns out to be b=1/2*π*h to come exactly to the golden ratios for the surfaces. (b=base,h=height)
The mathematical argument concerning the discrepancies observed are meaningless. The dimensions of Khufu will have been perfect upon construction. Movement, over time will have resulted in said discrepancies. Enoch Pray
https://youtu.be/HiQ8l7Vbgic
Subsequent settling as well as temperature variations based on sun exposure to the smooth versus rugged surfaces of today –all would seem to allow adjusting minute variations between calculated and physical measurements. Robert O. Pritchard Cheboygan MI 5.13.16
The dimensions of khufu MAY have been perfect. I do agree with you though.
If the base was 440 cubits, 440/2= 220. Draw a horizontal line 220 cubits long, now off the two end points draw two vertical lines. One of the two lines at (220 * 1.62) 356.4 follow that radius to where it intersects the other vertical line. From the horizontal line to the intersection it is 280.3943 cubits.
You can do this with a square. PHI and a piece of string.
http://www.stefanides.gr/pdf/2012_Oct/PHOTO_12.pdf
p.stefanides
I find it quite interesting that there have been no plans or blueprints found of the great pyramid as the Egyptians were meticulous when it come to writing. surely they had plans in which to work from?
Maybe it wasn’t the Egyptians who planned and built it.
I think you are correct.I don’t think the ancient Egyptians build the Great Pyramid or the Sphinx.I think they were build by some advanced civilization either living on Earth or from another place in the Universe.
The civilisation that existed in Noah’s day (before the Great Flood) was INCREDIBLY advanced. It is doubtful they were as advanced as us, but they had knowledge of earth science, physics, and metallurgy that still confounds our scientists of today. For example, in the current study of the remains of Noah’s Ark, researchers discovered metal studs used in the construction that are made of steel, platinum, and aluminum. The latter of which is not even found in nature. Also, in an dated story that made the newspapers in the early 20th Century, someone living in Chicago found a hand bell encrusted in a lump of coal. It dated back to the same Antediluvian Period of history, and not only did the bell still ring perfectly, its composition was of two metals that metallurgists today say they cannot be combined. Yet the pre-Flood civilisation was able to do it. Incidentally, the length of Noah’s Ark is the same exact number of cubits as the height of the Great Pyramid. The slope angle of the Great Pyramid is related to the speed of light (not Einstein’s calculation but the perfected speed of light mathematically discovered in the early 1970’s). Just those two pieces of information are too coincidental to be dismissed as accidental. And then there is all the modern research that has shown how the Great Pyramid is actually some kind of machine to generate power. Thanks to the inventions of aeroplanes and modern navigation instruments, a number of pyramids have been uncovered in the last 80 years. One underwater off the coast of the Bahamas, and another underground just east of Anchorage, Alaska, to name a few. After all these millennia, still generating power and emitting an electromagnetic field that made magnetic navigation instruments go wonky. Scientists, unable to understand how exactly the pyramids worked, were at least able to disable them (so no more planes and boats getting lost at sea). Whatever that pre-flood civilisation was, one can only speculate what other technology those people had (flying craft? genetic experimentation?). In any case, regarding the question of “who built the Great Pyramid”, my money is on them. To generate wireless electricity and/or generate a worldwide A440 harmonic resonance, who knows. It just really stinks that all this information and research and knowledge has been surfacing since 1900 and yet we STILL cannot purchase a Powermid Mark III for our homes. No working replica of the Great Pyramid has ever been attempted, nor has any corporation tried to develop the technology. It is a bit odd. >:\
Metal studs from Noah’s Ark? You must be referring to Ron Wyatt’s “find”. Or didn’t you know the ark was “discovered” AGAIN 3 decades later in another location. Sorry, Mark, but Noah’s Ark has not been found, and Ron Wyatt’s discovery has been disproven. You might find the following Web site helpful: http://www.tentmaker.org/WAR/
All that aside, yes I agree the Great Pyramid is one heckuva piece of engineering and a mystery. Besides the possibility of it having been built by an ante-deluvian race, there is even a theory that says a pre-Adamite (pre-Adamic?) race built the pyramids (plural meaning the Great Pyramid and the now-underwater ones). There are quite a few fascinating books on this subject, as you probably know.
It is the Atlantean civilization of which you speak.
simply we are not alone
They probably just got rid of them so robbers wouldn’t be able to get into the tomb that held the pharaoh and his treasure.
Ahh,… the tomb was empty.
No mummies were ever found in a pyramid. This is man’s attempt to catagorise something that can not be explained. Usually gets put in the religious box and everyone seems happy with this explanation. Greeks and Romans both studied in egypt and took the knowledge into the wider world .This is where sacred mathematics, geometry were learned…plato…platonic solids, pythagoris etc….
There are Egyptian figures all through the region…of course they built it. Romans and Greeks learned mathematics, religion, “government” agriculture, and self-defense from them. The tradition of learning was mostly oral and done by doing, not necessary by writing everything down.
The Egyptian culture was well advanced hundreds of years before anyone else “discovered” the Pyramids and Egyptian culture.
It was very different from the other “Egyptian figures all through the region” in that it did not have any hieroglyphics or drawings of any kind, and its tomb was empty — no mummified remains, not even treasure was found. In that sense it was not Egyptian. The only thing Egyptian about it is that it is located in Egypt.
i think aliens built them
the Egyptian beings were of high enough consciousness to even understand the illusion of death, time, and life. They were beings so perfect, so divine, structural planning was beyond them. they had a mentality so powerful, and hearts so true, they did with their minds, not paper.
There are three possible culprits for the design and construction of the Great Pyramid. They are:
Father Abraham who came out of Ur and brought with him the secrets of Astronomy.
Joseph, who was sold into Egypt who was trained by Jacob/Israel in how to read Hieroglyphs.
And someone so bizarre that it’s unthinkable to the Archaeologist’s mind. A far out, far away, lost Civilization that had mapped the Earth’s longitudes with the same precision that we have. We used time, they used the Precession of the Equinox.
Eldon, I truly do believe, after a great deal of research, that ancient people in Europe had a hi order of mathematics and geometry as far back as 25,000 BC or even from Africa ( Blombos cave, ochre stone) and also had “signs” as a very basic language, that are found in ancient cultures around the world ( waves, circles, dots, swastika, etc). If we can have genius’ then they could have too. Many hi IQ people today have Schizophrenia, Aspergers, etc and a few exceptional people who are mentally healthy- In other words people who see the world from a different perspective. The ancients could have had a few that passed on their knowledge and eventually became a nomadic priesthood (astrologers) that left monuments (pyramids, circles, etc) everywhere. About 3500-4000 BC S at Skara Brea there were found 5 types of small carved balls that represented the 5 Platonic Solids ( all matter in the universe can be made from these basic shapes). These were made about 3,000 years before Plato. They could have come into Europe from anywhere, but possible thru Spain around LGM.
i think Enoch the shepherd king built the great pyramid of giza
Pyramid architecture is surprisingly advanced, but modern science tells what man is able to accomplish, so it may have been our world civilization building these amazing structures of advanced knowledge. The site at http://1008anand108.page.tl shows some of the mathematical perfection by the reorganisation of the ancient yantra mandala as pyramid architecture, closest to sun pyramid in Bosnia perhaps. However, when and who was building it we do not know, because later clues may be just showing one period of time. We plan to build by pyramid architecture a climate ship as Pyramid Architecture Universitas Academy, and welcomes people wanting to form the Academy to join in.
Well, i am pretty sure you will dismiss the truth for that it is too far from the classic academia that is based on false “facts”.
Anyhow, here it goes and whoever wants to look into it, may the light be with him and show him the way further ahead.
I will not provide evidence, just the hint and whoever dissagrees or gets upset or even goes ballistic let that be his own problem. I don ‘t care about whatever nor be willing to debate.
The creators of the Great Pyramids were living in the age of well before the Great Flood.
Most possibly if not certainly they were ancestors of what was later to be the people of the Cretan Civilisation with origin from that same island that is called Crete nowadays.
I know i know…. i told you, only a hint and no proof but fir the seeker of truth that should be more than enough to investigate and debate for himself.
Sad thing though is that classic academia does not offer much matterial to the direction required making ones study on the matter kinda tricky and hard if not impossible since the right clues are hidden or missinterpreted by the ones of “other” interests.
Peace and keep your thoughts inside whatever the case.
The Pyramids will show in time that they were tools of knowledge and technology used for the wellbeing of the peoples and the generations thereafter, being something like a poorly understood book for where we are brought nowadays.
In short, the pyramids were build by the Old Cretans which have a living bloodline still much clean to our days. In other words the Pyramids were built by the Greeks if we want to make this more relative to todays terms before the Great Flood. Much before that.
By the way to comment on the Atlantians as they were brought up…
Just to stir a few minds into productive thinking.
The Atlantians were of Greek origin but occupied a different sum of areas far from Greece wich was not what is shown by modern map borders but much much greater than modern supressed Ελλάδα.
As such it was to the west of modern Europe and the signs of that departed Greek civilisation named Atlantis, albeit making important civilisation and technology steps after many hundreds of years, was found out of ballance in respect to the Έλληνες that were of the original line and in the basic greater part of the classic Ελλάδα. That basic central part of Greece was surrounding all if the Mediterranean Sea and going far far into the adjasent lands.
So when the Atlantians to the west of modern Europe went out of ballance they thought that it would be a great idea to make war with Greece. You see after many many aeons it was basically dissmissed or forgotten that they were of the same origin and thought they would be better and thatvtheyvwere different.
So it happened. Long before the Great Flood.
And they lost to the Greeks….
as they were still inferior in many key and basic values no matter the technology… just like today where people just think but do not know.
I bet they did not teach you this at school or university…
No mattet what you think, if you look into it you will see…
Take care and as i said : PEACE !
I also notice the ratio in courses to width in the grand gallery. 22 steps, at 7 ft of width.
I discussed this in respect to resonance with Christopher Dunn in Glenview Il in 1999.
I never heard back on that.
Interesting to see this article repeat the same (and understandable) erroneous conclusion drawn by many previous works regarding the Great Pyramid and the supposed deliberate occurrence of Phi in its dimensions. In fact, the occurrence of Phi was an inadvertent by-product of the deliberate use of circular proportions in the structure, by its Old Kingdom Egyptian architects. The circular proportions (which explain why Pi is observable) were thought to bestow encircling ritual protection on the monuments, and this was included deliberately there and on other pyramids and tombs, and in the proportions of the Great Pyramid’s tomb chamber. Egyptology Professor Petrie, Verner, Edwards and myself (background in archaeology and engineering and studied this for 10 years) all concur on this point. It was circular proportions that determined the shape of the pyramid at Giza for Khufu, not Phi or any Golden Ratio, which were culturally unknown and even irrelevant for the Ancient Egyptians whose life was based on practical, functional geometry and basic symbolic systems.
SEE HERE FOR a website that discusses some research I carried out on the Great Pyramid with the National Museum of Scotland recently:
http://arkysite.wordpress.com/2013/05/07/the-edinburgh-casing-stone-a-piece-of-giza-at-the-national-museum-of-scotland/
Dr Dave Lightbody.
Actually, the article concludes with this: “It’s possible though that the pyramid dimensions could have been intended to represent only one of these numbers, either pi or phi, and the mathematics would have included the other automatically. We really don’t know with certainty how the pyramid was designed as this knowledge could have existed and then been lost.” There’s still much we don’t know about the pyramids, and there are those who disagree with the traditional beliefs held about them. I respect your work and viewpoint, but think there is merit in presenting viable alternatives for the reader.
Dr.lightbody…..I am sure your a busy man but I truely need to discuss some very important issues that I think I have answers that I just came across the last couple months…your article here is part of it and I think you may understand me on this one….I look forward to speaking with you if you choose so..take care Mark…..markd.worrell@gmail.com
You state that “phi is the only number which has the mathematical property of its square being one more than itself.” This is not true. If you solve the equation x^2 – x – 1 = 0, you get 2 solutions, one of which is phi. The other number is negative and would be irrelevant in constructing something. But to be accurate, you should probably change your assertion to “phi is the only *positive* number….”
That is partially correct. There are indeed two solutions. One is 1.618…, which is known as Phi with an upper case. The other is the -0.618, and 0.618 is the reciprocal of Phi, also often known as phi with a lower case. So both of these numbers are known as “phi”, with one of the solutions being its negative version.
Isaiah 19:19+20 In ancient Hebrew letters also had numerical value. If you use the measurements that were used at the time, the pyramid inch then the numerical value of the words in these 2 verses in Isaiah add up to be the height of the Giza Pyramid. The pyramid inch was derived by taking distance from north pole to south pole thru the core of the earth and dividing that distance by 500,000,000. The pyramid inch was also used in Solomon’s Temple and the arch of the covenant which is also the same exact measurements of the stone arc found inside the King’s Chamber in the Great Pyramid.
The Hebrew’s were in Egypt for how many years before Moses? I don’t see them changing their unit of measurement on their own. Heck, we can’t even go metric.
Study “The Battle of Kadish”. Canaan was part of Egypt at the time of Moses. Thutmose III fought a battle at Tel Megiddo (Armageddon) to secure or take back this land from the upstart Amorities. This land and lands much further north were Egyptian territory up to and past the time of Ramses II. The wilderness that Moses wondered were just outside of Egyptian territory. When Moses died the Hebrew’s reentered Egyptian territory. If the Egyptian army would have won the “Battle of Kadish” the Hebrew’s would most likely have been the occupying force. Moses never was “un-banished” from Egypt.
phi is mentioned as 256/121 the true figure is 196/121
The text above has been revised. Thank you for the correction.
They used a wheel to measure the dimensions of the base. They unknowingly introduced pi.
And perhaps they unknowingly aligned the pyramid to within 1/15th of a degree to true north too? Doesn’t the evidence more readily suggest a high degree of sophistication in their knowledge?
True north is not difficult for anyone who observes Polaris – which from Egypt gives a nice line on true north – or, for that matter establishes East and West at the solstice. I prefer a simpler solution that using wheels for measurement accidentally included the Golden Mean.
For that matter using ‘palms’ and ‘cubits’ could accidentally include the golden mean – our skeletons include the ratio also.
I am doing search work on music theorapy. I would like to construct a pyramid based on golden ratio. Size of the pyramid around 4 or 6 feet base. What should be height. Kindly guide me. also I would like to small pyramid about 4 inch what should be height.
Use the Golden Triangle above to make such calculations. It’s base is shown as 1, so the full base for a pyramid is 2. If you want a 4 foot base, you multiply the dimensions by 2. The base is then 4. The height is 2 times the square root of Phi, which is 2.544. The hypotenuse is 2 times Phi, which is 3.236.
Didn’t they say the great pyramid had 8 sides?
Here’s a link with some facts about it (number 12 is the one I mention): http://www.ancient-code.com/25-facts-about-the-great-pyramid-of-giza/
Simple experimenting will show that for a rectangle with given perimeter, maximum area is obtained if it is a square, and for a triangle the maximum area is obtained if it is equilateral. For a pyramid maximum volume is obtained if base is square and sides are equilateral triangles with sides same base side.
it’s almost funny how people in charge who have this information can hide it from the controlable masses and rewrite hystory, and supress knowlwdge…. but we are about to wake up.
A rectangle of given perimeter will have maximum area if it is a square.
A triangle of given perimeter will have maximum area if it is equilateral.
A pyramid will have maximum volume if it base is a square and its sides are
equilateral triangles.
This requires only simple math to arrive at.
No pi or phi needed.
That may be, but then the sides of the Great Pyramid are not equilateral triangles. The triangles on each side of the pyramid have a base with a relative length of 2, and the two other sides have a length of 1.618 (Phi). If they could have maximized the volume or surface area by using equilateral triangles, especially given the high cost of construction, then why didn’t they do so?
Do you guys make pyramids to these exact dimensions or know someone who does?
I’ve heard that the Great Pyramid is also 8 sided to signify the equinoxes. I saw a documentary that included some history, but mostly about the Pyramid its’ self. In it, there was a photo of the Pyramid taken from a plane a few years after the second World War, during the equinox, and it clearly showed that half of each of the two of the sides facing away from the sun shadowed on one half and (sort of) light up on the other, and that this can not be seen during the rest of the year. Do you have more information about this? I can not seem to find that documentary again.
Think of the Pyramids as Foundations of Palaces, Human timeline of 10,000 years people!
Primary concerns of mankind was,is and always will be are Ownership and Orientation that leads to counting,calculation, navigation and astronomy to start with mankind knowledge.Signs for counting(numbers)lead phonetic signs(alphabet)through out the History.
Early use of pen and paper as well as tools goes back to civilizations in Asia and Africa because of easy access to natural facilities like minerals,texture of soil,open skies and so on.
Historical documents are not quiet referable.
We should not be surprised if Chinese,Egyptians,Indians,Babylonians or Persians knew about Square roots or Divine proportions as leading nations, since when a curious person starts measuring shadows as natural time peace in different times of days and seasons and makes breaks for constructions and studies it’s diagonal proportion he will come up with,not so miraculous.
The fact that the pyramid faces true north and during the spring and fall equinoxes the pyramid shows 8 sides from the sky is enough to baffle anyone with any sense of wonder. forget the fact of the impossible feat of its construction, its mathematical and symbolic properties is enough for one to realize this is the work of something divine.
COMPARE:
http://www.stefanides.gr/pdf/2012_Oct/PHOTO_11.pdf
WITH
http://www.stefanides.gr/pdf/2012_Oct/PHOTO_12.pdf
Regards from Athens,
Panagiotis Stefanides
Can anyone help me with the ratio of base to ridge dimensions of the Cheops pyramid, please?
Thank you!
Those dimensions are presented on this page. The Great Pyramid of Giza is also known as the Pyramid of Khufu or the Pyramid of Cheops. See http://en.wikipedia.org/wiki/Great_pyramid_of_giza.
Thank you, Gary. That is a good reference. What I am looking for is the base to ridge ratio, i.e.,base equals I, ridge equals X. I see lots of references to height, but haven’t found the ridge length.
This simplest solution is likely to use the Pythagorean theorem to calculate it: Ridge = the square root of (base squared plus height squared.)
Oh, right! Thank you Gary!
I’m building a 10 foot pyramid on a four foot wall to house my astronomy gear and observe from. It’s a fun project, and will be real cozy this winter.
Best regards…Bob
I wonder if a combination of these schemes was used.
Such a coincidence otherwise..
https://drive.google.com/file/d/0B637hKjsUvvMVnVHdms5OVR4UTg/edit?usp=sharing
its intersting to see that some of the things that we just grew up knowing that they are there,actually have an origin………….
Have added a pyramid calculation using phi pi and e. Hope its interesting.. let me know..
https://drive.google.com/file/d/0B637hKjsUvvMaDZKXzNMRTUzbGs/view?usp=sharing
Thanks.
In my opinion, great pyramid of khufu means low golden section transform which is a class of orthogonal transform in mathematics, see my ppt 🙂 http://www.slideshare.net/jasonli1880/great-pyramid-of-giza-and-golden-section-transform-preview
The actual dimension of great pyramid Giza is in Holy Quran.The verse 28:38 is the main verse regarding pyramid. The verse is in sura 28, verse no 38, total word 27 ,letters 103 and gematrical value is 6157. Add the nos.28+38+27+103=196. Now 6157=3.14×280.11×7. Here 280 is the hight of great pyramid in royal cubits.Again please devide 6157 by 7 it becomes 879.57 which is twice the base of pyramid length. If 6157 is devided by 196 , it becomes 31.4132…..which is 10x 3.1413… Please compare this value from international survey.
The angle of slope 51.8272923730° is acos(phi) –> cos(51.8272923730) = phi = sin(51.8272923730)^2.
according to http://milan.milanovic.org/math/english/golden/golden3.html
after calculations …
“The Great Pyramid turns out to have the same perimeter length when measured in a horizontal plane, as a square, and in a vertical plane, as a circle.”
In your example (pdf) :
Perimeter as a square = 4*2
Perimeter as circle = 2*pi*sqrt(Phi)
Means pi = 4/sqrt(Phi) = 3.1446055110296931442782343433718357180924882313508929506596078804047281904892436548476515566340325422
In Figu forum for example you can find the same result http://forum.figu.org/us/messages/863/8884.html?1205193138#POST31322
Giza Height : 152.9553357
Elements in the universe * Giza Height * 7 = Speed of light
280 * 152.9553357 * 7 = 299792.457972
http://www.futureofmankind.co.uk/Billy_Meier/Contact_Report_127
As Jain said there is a fight between the west and the east about Pi.
http://www.jainmathemagics.com/page/10/default.asp
here is an interesting article about “The Mathematics of the Great Pyramid:”
http://greatpyramidmath.weebly.com/25.html
The pyramid relationship does not necessarily have to mean that pi is defined as 4/sqrt(Phi), or 3.1446055… It can also just mean that the pyramid embodies the actual value of pi, 3.14159…, with a high degree of accuracy.
There are 2 claims about phi and pi in the pyramid.
1 – “The perimeter of the base of the Great Pyramid equals the circumference of a circle whose radius equal to the height of the pyramid.”
So : 4 * 2 = 2 * pi * sqrt(phi) –> pi = 4/ sqrt(phi) –> 3.144 605 511 …
2 – “The area of that same circle, with radius equal to the pyramid height equals that of a rectangle whose length is twice the pyramid height (sqrt(phi)) and whose width is the width (2) of the pyramid.”
Area of rectangle = 2 *sqrt(phi) * 2 = 5.088
Area of circle of radius sqrt(phi) = Pi *r^2 = 5.088
So : Pi * r^2 = 2 * sqrt(phi) * 2 –> Pi = 4* sqrt(phi)/ Phi = 3.144 605 511 …
Which means if (i repeat IF) those 2 claims are right pi is not 3.14159 but 4 / sqrt(phi) = 3.144 605 511
https://www.dartmouth.edu/~matc/math5.geometry/unit2/unit2.html
There are dozens of methods to calculate Pi to as many digits as you want, as shown at http://en.wikipedia.org/wiki/Pi. They’re all based on mathematically sound concepts, and all produce the same value for Pi. The pyramid’s approximate relationship to both pi and phi is very interesting, but the absence of its limestone skin make its dimensions subject to estimation. Why would anyone assume that unproven claims about the pyramid would unveil a more accurate value for Pi than numerous mathematical methodologies that all confirm a different value? Alternatively, can anyone prove that all the other methods of calculating Pi are wrong?
> Alternatively, can anyone prove that all the other methods of calculating Pi are wrong?
Yes.
You can let a comment after this demonstration that pi = 4/sqrt(phi) here :
http://www.veteranstoday.com/2015/02/05/pi/
“Please pass this article along and help us challenge the academics to adopt the correct value of pi”
Or prove the demonstration is wrong.
Try to contact me because when i had created my book(never been publish yet) just last year before i graduate college i was 19 when i first started now i’m 21 and studying mathematics just by myself…I had created a consciousness book related towards my experience and now that i read this site I was SHOCKED! about my findings that this Pyramid of Giza is created upon a mathematical perfection!…Upon my discovery that the Giza has never been finished on its top portion and I had the answer already and this 51 degrees related also towards my findings is very accurate and related towards everything beyond the cosmos…Wew this is Epic!!!
I think the great pyramid and the sphinx as well as the other artefact dotted around the world such as the one in Peru and Easter Islands were built by an advanced civilization who once inhabited the earth. The Egyptians I think , dicovered the pyramid. They did not know who built it. That is why they don’t have any records.
i find it very interesting but my doubt is that how is it related astronomically.
Hello everyone! 🙂
I made a video about the Great Pyramid, the number Pi and Phi…
The link : http://www.youtube.com/watch?v=dp31oVdIfek
Goodbye! 🙂
The ‘pi-theory’ is supported by people who argue that the Earth’s radius divided by 432 gives the pyramid height (ignoring some zeros). They claim further that 432 is a very “significant number’. One can agree that, as it is the double of 216, it has some interesting properties but that is another story, probably.
The ancient yantra or perhaps also David star, see my homepage; http://www.1008-108.webs.com, I have perfectionated and possible this is lost pyramid architecture. Is phi and golden values found here, too, after al the perfection was found by the relationship between circle and square? Please send answeres also as mail.
cheers Anand
this is super cool man you know what’s better nothing it is fully sick ya
OMG everyone its MJ holy moly SICK
A triangle with 2 equal heights and minimum perimeter gives two equal angles whose cosine is 0.6180339887 51.8272923729º is Phi – 1 proportions that we find the Great Pyramid.
http://triancal.esy.es/?y=345.90660621318&z=345.90660621318&p=1151.9349550497
If you click on the “draw” button and marks the notable elements get the approximate position of the secret chambers, perhaps in the orthocenter there is some yet undiscovered.
http://triancal.esy.es/HTML/GG.html?C=0.90455689430235&B=0.90455689430235&a=439.9999999999
comment point everything to say the people of the Afrikan Continent did NOT reach such heights..very sad…esp when headed up the great Hapi, u basically find the evolution of pyramid architecture with Giza being the culmination…gasp, cant be…they’re BLACK…smfh aliens only did it because of all the evidence on tv…
I’ve never heard anyone refer to limitations of our human ability to construct the pyramids to have anything to do with race. Without specific evidence it would be wrong to assume so. The feat of their construction is just beyond what we know any humans to have had at that point in history, and is unexplained today. Race has nothing to do with it.
Hi everyone,
What a great debate. I might be jumping in a bit too late, but I was looking for some advise.
I wanted to create a pyramid using the golden ratio number only.
Would be something small, from 10 to 20 or 30cm height, but I wanted to be constructed using the golden ratio numbers.
I need your help to make it as accurate as possible using this method.
I wanted to be perfect all the way, from the angles to the smallest detail.
Can anyone please help me around, providing me the exact measures to be used, in a simplified way, so I can pass it on to the fabric?
Thank you.
As in the illustration above, the sides of the golden ratio-based pyramid have these relative proportions:
Base – 1
Height – Square root of Phi (1.27201964951…)
Hypotenuse – Phi (1.61803398874…)
If you want a height of 30 cm, just divide that by 1.27201964951 to get the base of 23.585 cm and multiply it by 1.27201964951 to get the hypotenuse of 38.1601 cm. Use the template at https://www.goldennumber.net/wp-content/uploads/2012/08/great-pyramid-golden-triangle-template.pdf to create a pattern that will fold to create the pyramid.
Thank you Gary.
What kind of beauty hidden dimensions impossible to see if you don’t know “The secret letter” of the ancient builders. Pharaohs were putting their names in the dimensions of the pyramid and thus were given the development of immortality. Nobody can delete the “names” of dimensions.
One of the reasons why there is no text in the Pyramid, the texts are put in the dimensions.
They used Pi to these values: root8 * (10/9) = 3,142696805….
Why? Archimedes said Pi is between this value 223/7 > Pi < 22/7. Between these two values we have an infinite number of values, but only one value can be geometrically constructed "with a divider and a ruler unmarked" this is number 3,142696805…..
Each pyramid is a unique work of art, which carries your message.
first, : “Khufu pyramid size” on youtube
I have been working on Egypt and Giza for the past 8-9 years. Based on my research I have concluded some new and interesting facts that will make the real purpose of the existence of the pyramids clear.
This week I have put a film about Giza, and the time of Giza on youtube in English. I believe it should be interesting for You.
https://www.youtube.com/watch?v=FmHFBgfl7G0
I would greatly appreciate if you would take time to watch the 40 minute long film and perchance reflect on it.
the others:
Khufu’s calendar on youtube
Giza the time machine-World Mysteries Blog on youtube
Sincerely András Gőczey Architect from Hungary
I cannot find your video.
What I am seeing here is the Bible code.
I think if you want to know how the pyramids where built and have greater then math 85 skills you should consider yourself unqualified. The reason the sides of the pyramid line up with the north star is, at night someone stood at the center of the base and with a plum line marked the center of the north face, ran a string line from that point to the center plum line and the same distance to the center of the south face. Then took the same distances at 90 degrees for the center of the east and west walls. Now with the Great Pyramid there is no Pythagorean theorem used to find the corners (3, 4, 5). For every two units of measure to each face center use 3 to each corner. Now if you do this for each layer as you go up you will stay true. All you have to do is keep your center point.
I have worked in the stone business for 20 years. It is my understanding that the reason that the Golden Ratio shows up so often is it just looks right to the eye. I try to incorporate it in my creations, not because of some cosmetic connectivity but because it draws the eye for just a bit longer.
Now the building blocks of the Great Pyramid are laid with different thicknesses to the courses because each ledge of stone is different as it sits in the ground. What I put to you is, with the casing stones what height at 51_52 degrees need to be to maintain the same unit of measure so the 2 to edges and 3 to corners without changing the unit of measurement.
The key to the Great Pyramid is they used the K. I. S. S. Principal.
You should be well aware that laying courses in such an irregular fashion is simply impossible with ancient or modern standards. Are you saying that you can do this? You have the technical capability to do that?
All this about the EXTERIOR of the GP and the layout of the plateau. Please look at some of the INTERIOR dimensions, mainly the Kings Chamber which also is built to a ‘rule’.
Newton was concerned with GP measures to try to help him straighten out the true shape of the globe and also a unit of measure.
And ONE other exterior point. The Apothem of the GP is about 185meters. This is an exactly fraction of a minute of arc AT THE PYRAMID.
I read half of the comments here and i have an interesting question for you guys.
We are arguing on how the egyptians the builders of these pyramids knew or didnt know phi?
The question is … hmm how can i put this? So many writings and symbols or any writing system they had.. were there any numerical carvings paintnings or whatever archieologists find due date tells us how did they count things? Cz using about 2.3 million stones to build a pyramid jeezz definitely they knew mathematics and i bet even phi and u know secrecy those days .. they had knowledge and only the ones with power got educated and kept for themselves for centuries.. the city of Iskandaroon the library which held all the records was burned .. well someone till now holds these secrets and as we all know nthng has changed from ancient times till now .. and that’s human nature with his good and evil intentions…
Im just asking it is impossible for one super genious geek to do this work… a system a unit who is well taught and organized could accomplish this kind of achievement so maybe we are looking from the wrong angle and not asking the right questions?
Looking at the pyramid and examining it ..we see that it is almost perfectly build with minor errors of mathematically calculations and alignments with earth and sky… so?? Earth and skyy … earth and upp upp to the sky pointing towards to the sky stars and they are the thombs for the pharoas? Hmm why they want to go up? Preserve their bodies? Magnetic field … and earth is ringing like a bell .. i think they knew mooore about pretty much of everything than what we know and learn 2day …
Delamer Duverus writes that the Pyramids were part of the Tower of Babel and were covered in glass of red, yellow and blue, the Pyramid at Giza being blue, and 2/3 were destroyed and which possibly made the Sahara as that was once the fertile plains of Mamre. The sphinx was carved out of the center structure which base looked like the Star of David and which came to a point. The pyramids would absorb the three colors of light, and reflect the cosmic sheath or energy which contained the 3 light rays towards the center structure, which would then direct it into outer space. This was a destructive energy.
Asorbing the light rays into the earth through the pyramids created the land of Milk and Honey. Unfortunately, what can be used for good, can often be used for evil, for the cosmic energy can be directed by apparatus in space, perhaps a parabola. The Book of Jasher mentions that there was something in space, and the builders went up one day, spent a year, and then came back the next day, which refers to time travel. This was a star wars weapon. Allegorically, Cain killing his brother Abel was also through similar structure, and Abel is asteroid belt between Mars and Jupiter.
He suggests that Man came to Earth to entermingle with those building the tower, because it was a weapon to be used against Man, and Man confused their tongue so it could not be completed, and then Man destroyed 2/3 of it.
The mathematics He says is all about squaring the circle, knowledge we do not have ourselves, but available in sextoid mathematics, which He won’t give us until we have learned to live in peace. Doubt that will happen with our insane government.
I’m sorry, a square, some string, a plumb bob, a level and something to mark cubits. Then all you need is an unobstructed view of the north star, which in not to difficult in a desert.
Not easy in a small scale, but as long as you can project the angle on the four sides (with the string/cord) I don’t see the problem with labor that just worked on the bent and red pyramid.
I ask you. What is the hard part?
Great Pyramid is based on hidden things that they copied.
That just changes the question. Who did they copy them from and where did those people get their technological insights?
Four couriers on the bottom plus one at the top = 5 corners. And the square root of 5 = 2.2360679775, .+ 1 = 3.2360679775 divided by 2 = 1.61803398875 = Phi.!
Maybe the builders purposely left the ancient and universal secret mathematical knowledge in the actual design of the Pyramid itself. Their reason being that the structure would stand the test of time and that means so would the knowledge it contains.
This is done so by building a working mathematical model on a massive scale with a near perfect design and architectural execution,
Building the pyramid accomplishes the goal of preserving and explaining the knowledge of this math by means of the structure.
This could help explain why there are no writings pertaining to the secret mason building,
Therefor, the great pyramid Is an organic diagram that if understood, is a textbook for the usage of Phi &Pi.
The balance and design of the universe is beyond complex reason and human understanding.
The Great Pyramid in all of its timeless wonder is a footstool to the Heavens.
Using feet or meters is a fool’s effort. The ancients didn’t use those measurements so there’s no reason that we should. It only makes sense that they would have laid out the dimensions in whole, easily measurable units.
The basic unit used was the cubit. There are several existing relic cubit sticks which average 20.7 inches in length. Each stick was divided into 20 sections of fingers, palms, hands, fists, etc. These 20 divisions allowed 85 different angles to be accurately laid out.
We can see using conversions that the base of the pyramid was laid out as a square with sides of 440 cubits. The slope of each side was measured at a ratio of 14::11 which is an angle of 51.8428 degrees. The 14:11 ratio equals 4/pi (when using the supposed value of pi at the time being 22/7).
There’s no evidence that the full original plan dictated what the height would be but when the base and face slope were maintained, the height came out to be 280 cubits. Once the base was set and the slope of the faces was set and maintained, everything else just fell into place.
The base length of 440 cubits is 759 feet (440 x 20.7 / 12)
The total height of 280 cubits is 483 feet feet (280 x 20.7 / 12)
Missing stone at the base, the missing casing stones and the missing 20 feet or so at the top make it nearly impossible to make accurate measurements now but, as mentioned, the Egyptians almost certainly used whole number measurements in cubits.
One other whole number relationship is the angle to vertical of the corners. The ratio (height 280 / half the base diameter of 622.25, or 311.125) equals .9000. This ratio, 9:10 gives a corner slope of 41.9859 degrees, which is as actually measured.
Arguing on the dimensions does not get us anywhere. The wonder is that the pyramids are found all around the world across all the cultures. These are mostly made of accurately carved, large stones. Over thousands of years, these monuments have proven to be cataclysm (weather, earthquakes, floods, atmospheric effects, etc.) proof. This is the real wonder and the question is who taught this to the people, supposedly living in caves (why would they even live in caves, if they can build things like this) and the only tools they possessed were copper chisels and hammers, and stone knives (copper and stone tools cannot cut granite which is extensively used in many of the ancient buildings)? Why do we believe everything that Plato said except his description of Atlantis? Why do we believe in certain accounts of history and not the others? What makes us believe that many of these including Sumerian cuneiform tablets and indestructible Emerald tablets of Thoth are merely myths?
A mainstream Egyptology scholar recently stated that pyramid’s mysteries can only be solved by Egyptologists, not by engineers. That is not correct he most know that engineers create, designed, and built the pyramids. Egyptologists came after millions of years to study and evaluate the culture that built the pyramids. Besides, it is known that Egyptologists can read papyrus, but engineers can read designs and structures of buildings. Egyptologists never have found, or re-designed the great pyramid’s construction plans. What they have done is to create its “as built” plan”, based on actual measures of the structure. To design the structure means to establish its specifications, geometric requirements, and the materials dimensions and strengths required for supporting the buildings. As known, these are tasks which the Egyptologists are not prepared to do.
It is known that the great pyramid was designed and built about 4,500 years ago by an Egyptian culture, named the pyramid builders. Since those times, its construction plans have never been found or re-designed by any Egyptologists or scholar. From another point, and as something important, and incredible, a Puerto Rican professional civil engineer, Samuel Laboy, presents to the world the entire geometric plan of this great monument, as designed and built by the Egyptian engineers. To solve this mystery, he conceived and designed an architectural geometrical template, which he found was used by the Egyptian designers.
Engineer Laboy, copyrighted his template in USA and Puerto Rico, as the perfect symbol, composed of the figure of a circle, a triangle and a square in a special geometric arrangement which permits special properties for general designs. He used it to design the entire pyramid, including the original entrance, descending passages, the antechamber, the king’s chamber and its five ceilings, the queen’s chamber, the grand gallery, corridors, the subterranean chamber, etc.
Engineer Laboy originally developed, without making reference to the great pyramid’s dimensions, a dimensionless plan of the entire pyramid. When finished, the radius of the template circle is set up using any unit of measurements, and all the dimensions of the dimensionless plan of the pyramid are calculated. The entire plan will be expressed in the same units of measurements as used for the radius. Since the designed plan is developed by a geometric process and all dimensions correspond proportionally to those of the great pyramid, it means that the pyramid’s dimensions were dictated by geometry and not defined by the Egyptian builders. Only one number is required for the radius of the circle, therefore, only one number will generated all dimensions of the great pyramid, and it has to be the correct one. Other numbers will change the dimensions of the pyramid’s structure.
Surprisingly, the product of 153 ft. Multiplied by (pi = 3.14159) = 480.6637 ft. Is the correct radius which corresponds to the pyramid’s height. After a comprehensive and detailed comparison, the designed plan of engineer Laboy proved that it corresponds, section by section, to the entire great pyramid’s structure dimensions, characteristics, and properties. His geometric designed original plan is available at amazon (24 x 36 inches).
In addition, engineer Laboy also designed the geometry of the pyramids of Chephren, Micerinus, the Red, the Bent pyramid and others. The results of his designs were exactly equal in dimensions, characteristics and properties as the built structures. Engineer Laboy is the author of “A Civil Engineer looks at the Great Pyramid (390 pages) and a supplement book of 160 pages, additionally he presents a DVD video of 3 hours and discusses his entire design work.
Sorry sir, this is not span, a theory or an idea. This is something real. I understand this is incredible, but this is the end of your trail of tears to find the original design plan. This are my results of my virtual thesis in Oklahoma State University started in 1970 and ended in 2010. the books and DVD and designed geometric plan exactly matched every exterior and interior dimension of the structure of the Great Pyramid work done without any reference to the Monument. You are doing too hasty to consider it as span. Just check my websites, check Amazon.com, see YouTube where I have uploaded 25 videos, some of then more than one hour in time. they are free to view and download. My references include engineers, architects, Egyptologists of more than 30 years, contact the evaluator of Egyptian designs Marshall Payn who had worked in Egypt. Just ask “Google” who is “Samuel Laboy”, and also view this the following mentioned video. there are two additional videos. the first presents the entire designed of the Great Pyramid, the second part in YouTube, the comparison between my designed plan with the official measures of the great pyramid showing they are equal, the third, additional references to validate the results. I am a professional civil engineer who have dedicated 40 years to study and investigate the Egyptian pyramids, worked for many years as engineer in charge of bridges and road constructions, has 3 patents granted by the USA Patent office and received the highest award given by the Government in 4 different occasion. I visited the 3 Giza’s pyramids, including their interior for several days. You can email me at egipto153@hotmail.com where with pleasure I can answer any other question or reference.
All this information has been sent to the Egyptian authorities, but unfortunately, no answer has been back. Check THE PAGE “MINISTRY OF ANTIQUITIES”
My video “Modern Evaluation Of The Great Pyramid” – Part I – YouTube, and Part II, and III
MODERN EVALUATION OF THE GREAT PYRAMID PART II
Samuel Laboy – Mathematical patterns of the Great Pyramid: A civil …
https://eduardopiperet.wordpress.com/2014/03/01/samuel-laboy-mathematical-patterns-of-the-great-pyramid-a-civil-engineer-looks-at-the-great-pyramid-of-giza/
Mar 1, 2014 … For many years, we have heard and read about the Great Pyramid of Egypt … can be created in any part of the world, with no reference to the pyramids. …. Video: Modern Evaluation of the Great Pyramid (2 hours 20 minutes).
MATHEMATICAL PATTERNS OF THE GREAT PYRAMID – eduardopiperet.wordpress.com
Samuel Laboy – Mathematical patterns of the Great Pyramid: A civil …
https://eduardopiperet.wordpress.com/2014/03/01/samuel-laboy-mathematical-patterns-of-the-great-pyramid-a-civil-engineer-looks-at-the-great-pyramid-of-giza/
Mar 1, 2014 … For many years, we have heard and read about the Great Pyramid of Egypt … can be created in any part of the world, with no reference to the pyramids. …. Video: Modern Evaluation of the Great Pyramid (2 hours 20 minutes).
Why is it that, despite the fact that the “pyramides” are much older than Pythagoras, Westeners still want the mathematical calculations used to build them to be credited to an European who spent over 20 years learning in Africa? Is it a matter of an intellectual dishonesty? Or is it just ignorance?
I agree hold heartedly . The mystery schools of kemit alps taught electromagnetism
Because the antique books on “Euclid’s” geometry, which cite “Pythagorus'” theorem, candidly state [in the appendix], that even though Pythagorus’ theorem goes back to a couple thousand years before Pythagorus [most anciently in China] only the Greeks [as Europeans] merit mention. In short, it’s predicated on Victorian English racism. [From the appendices of Euclid’s Elements]
thank you i am from egypt and i always wished some would say that
READ MINISTRY OF ANTIQUITIES -SAMUEL LABOY
Ministry of Antiquities – Home | Facebook
https://www.facebook.com/Ministry-of-Antiquities-336764893195328/
THE DOCUMENTS PRESENTED BY SAMUEL LABOY IN RELATION TO THE …. Barcelona legend Carles Puyol visits the Grand Egyptian Museum and Giza …
SEE MY NEW DISCOVERIES ABOUT LEONARDO’S DRAWING
DAVINCI – YouTube
https://www.youtube.com/watch?v=P6KrJCz0Zaw
May 6, 2012 … SEE MY NEW DISCOVERIES ABOUT LEONARDO’S DRAWING: THE FIGURE … + Samuel Laboy oh about the vitruvian man.. i used the leonardo’s …
SEE MY NEW DISCOVERIES ABOUT LEONARDO’S DRAWING
DAVINCI – YouTube
https://www.youtube.com/watch?v=P6KrJCz0Zaw
May 6, 2012 … SEE MY NEW DISCOVERIES ABOUT LEONARDO’S DRAWING: THE FIGURE … + Samuel Laboy oh about the vitruvian man.. i used the leonardo’s …
Er…
Looking at the picture of the folded circle:
It seems to me that all you need is to determine the height that you want your pyramid to be and the thing builds itself.
1. Determine your desired height.
2. Cut a piece of string to that height.
3. Tie the string to a stick planted in the sand at the center of your future pyramid.
4. Walk the circle dictated by the string which will serve as its circumference.
5. Draw a square which touches your circle at 8 symmetrically distributed points as indicated in the picture above.
6. The square tells you exactly where the edges of your pyramid need to fall and you know the height – the rest is simple algebra.
The Egyptians wouldn’t need to know anything else that this post hoc analysis points out – all of the *interesting* geometrical attributes of the pyramid are the *necessary* geometrical attributes of a golden pyramid, which comes about almost unavoidably once you determine how tall you want it to be. All of the imagined complexity is only inferred after the fact, the method seems painfully simple.
Take a look again at your step 5, which says “Draw a square which touches your circle at 8 symmetrically distributed points as indicated in the picture above.” Therein lies the challenge. You could come up with a variety of sets of “8 symmetrically distributed points.” Only one set will produce a pyramid with the proportional characteristics of the Great Pyramid, so you need to have an exact plan for the position of those eight points BEFORE you can do anything else in your approach.
Ah, missed a step. However, the golden ratio is not all that remarkable a relationship – if you play around with geometry long enough, you are going to stumble upon it. Given any arbitrary height or base, calculating the other is a trivial matter.
The method of tracing out the circle with the same radius as the height just simplifies the surveying process and helps direct precisely where the edges need to fall while requiring minimal technology to get it done..
It also seems that you can get a pretty good approximation of true north just by following shadows across the ground.
I guess I’m just missing what is so remarkable about the planning of any of this.
I guess you’re just not seeing the golden ratio as others do. Kepler called it one of the two jewels of geometry, yet you see it is unremarkable. I would say that the fact that it can be derived from so many geometric constructions, limits and series that DOES make it remarkable. In addition to that it appears in an amazing number of surprising places in nature. What other number do you know that has that quality?
Here’s another approach that gets you in the same vicinity without needing to know anything about phi or pi.
Start off drawing a square with an edge length of 230.4 meters. Use an edge of this square as the hypotenuse of an isosceles triangle with its apex at the center of the square. Each leg of this triangle will be 162.9 meters. Take 90% of 162.9 and you get 146.6 meters.
This method gets a ratio of height to breadth of 0.6363, with the height being ~ 0.07% off of the quoted height of 146.5.
Given that we are using an assumed height from Wikipedia, and the distances quoted are rounded to half-meters, it seems more reasonable to assume that the Egyptians simply knocked 10% off of a number determined by their base edge length than it is to assume that they employed any geometric constants. In either case, we need to assume that they rounded to the nearest half-meter when they built it. The benefit to this method is that it requires no knowledge of the Pythagorean theorem nor of pi or phi.
I would have loved to have been at that committee meeting. The ancient Egyptians are planning the world’s largest structure to entomb their Pharoah for his journey into the afterlife. They’re aligning it to many important celestial markers. The Pharoah asks “how high will my pyramid be?” The lead architect says, “Hey, how about we just knock 10% off the base length? All in favor?” The Pharoah says, “Well, it is about time for lunch. Yeah, that sounds good enough. Motion passed.”
Its easy to see why they chose a phi triangle.
If the triangle were steeper it would tend to collapse outwardly (like the bent pyramid), and if the triangle were shallower it would tend to collapse inwardly. So at phi its perfectly balanced and set to last millions of years.
That’s a very interesting theory. I’d like to see if any of the engineers in the audience can prove it to be true with some sort of structural engineering analysis. Any takers?
I am in a research for more than 60 years, about who discovered or created 360° ?
Because I have come to investigate taiji, pyramids and quadratura. Lights is part of it, light is not a speed but an angular pulsation, which today can be calculated with pytagorean theorem.
As I noticed in keops situation as it has been suggested : latitude = omega (celerity = c) sqrt(1/mu x epsilon) =29.9792458, but if you look at the longitude N 31.4159265 (which is my équation of omega (chiracécité =ç) sqrt(1/u*s) or sqrt(1/L*C) resonance frequency, one can notice it has shifted from about 10 kms (I have yet calculated exactly), which would give us a good approximation of the deviation in times (about 10000 years), I don’t know if these people new frequency but we know !
You can thank the Sumerians and perhaps other ancients for our 360 degree circle. Here is some more information:
http://www.storyofmathematics.com/sumerian.html
https://usatoday30.usatoday.com/news/science/wonderquest/2002-06-21-circle.htm
I’m not shure of what aishen means but….
Longitude ( E-W) reference point in Greenwich London England was established in the 1851 and can not have any meaning to the builders of Cheops.
The answer is more simple than all these add-ons after the fact! The ancients were enamored of their base 60 numerology. I believe it was based on number of days in the year rounded down to 360. That number was attached to the circle. When the radius of a circle is used as a chord around the circumference,
SIX EQUILATERAL TRIANGLES magically appear and even more remarkable each corner of each triangle is
60 degrees. Base sixty is still being used today; sixty seconds in a minute, sixty minutes in an hour, six times sixty in a circle. Sixty and its permutations are a magic number derived from the heavens. When you align four equilateral triangles on a square base, something magical happens. The internal angles form automatically without knowledge of PHI, PI, THE GOLDEN TRIANGLE or linear measurements. A further item of magic: 3 4 5 triangle is inside which provides the quarry men with a perfect tool to shape the slope of the sides. The KISS principle should be applied here (K keep — I it — S simple — S stupid).
As an aside, natural diamond crystals present as twinned pyramids (OCTOHEDRON) without knowledge of any of the above or anything else for that matter.
In essence, pyramids form naturally according to the laws of nature absent the folly of man.
Hi,
The area of each trianglular side is the base x height / 2, or 2 x√Φ/2 or√Φ. The surface area of the base is 2 x 2, or 4. So four sides is 4 x√Φ / 4, or√Φ for the ratio of sides to base.
They say twice a year at Spring and Fall you can see the Golden triangles in the great pyramid.. Making it eight sided if you are flying above it at that time. Although I had 2 years of math in high school it’s all Greek to me now at 88. I have been studying Astrology in relationship to the Holy Bible and I have found out if you take all the Astrology out you would have to toss the Holy book away, since it says that Astrology is evil, really not good. In Revelations it says if you wise enough you could figure out the meaning of the number 666. 60 was the base number at that time and still used today 6 times 60 =360 diameter of a circle and 6 time 360=2160 is our north pole drawing an imaginary circle which 2160 years for the end of an age. Well, Revelations transposed the number/.Then at the end Jesus said he was the bright and morning star (That’s our SUN you know) Of course God or Jesus didn’t say a word in the bible (They said they said)……..Oh, I could go on forever but I going to stop here………..
666 is in reference to one of the foundational elements of life within our DNA. 6 protons 6 electron 6 nuetrons, from what I’ve recently studied on the matter.
Sorry, but the math presented on this page is WRONG. If the base of the pyramid is 230.4 meters, then the “Phi to scale” figure for the height should be 230.4/1.6180339887498948482045868343656…, = 142.395…,
where Phi = 1.6180339887498948482045868343656… = (1 + sqrt(5))/2.
Actual height – scaled height = 146.5 – 142.4 = 4.1 meters, That is 100 TIMES LARGER than the amazing figure of about 3 cm you cited.
Your arithmetic is wrong. End of this claim.
Hi Dave. Thanks for taking a critical look at the page. I see you’re from the New Mexicans for Science and Reason, whose goal is promoting science, the scientific method, rational thinking, and critical examination of dubious or extraordinary claims. That’s a noble cause, but you need to make sure you understand the claims being made before being so hasty to summarily dismiss them.
Please take another look at the Kepler’s triangle on the page. It has a base of 1, a height of square root of Phi and a hypotenuse of Phi.
When the base of the pyramid is 230.4 meters, it’s the half base of 115.2 meters that corresponds to the length of 1 on this triangle. The height is then 115.2 meters times the square root of Phi (1.272019649514070) for a total theoretical height of 146.5366636. This varies from the Great Pyramid’s original height of 146.5 meters by 0.03666 meters, a difference of 1.443 inches, or 0.025%, as is correctly stated in the article.
I’m sorry, but the square root of Phi is NOT a “Golden Ratio.” Phi squared = Phi + 1, and 1/Phi = Phi – 1, but sqrt(Phi) is not anything special.
The Parthenon has a Golden Ratio (1.618…), but not the Pyramids.
All you have done is to find some tenuous connection between Phi and the pyramid. You new “Golden Ratio” of 1.272… is not Golden, It has none of the special properties of Phi. You can’t make a Golden Spiral using 1.272…,
Nice try, though.
Geez, Dave. The triangle has three sides. The other two of them – the hypotenuse with a length of 1.618 and the base with a length of one – also correspond to the proportions of the Great Pyramid to within 0.025%.
People commonly refer to triangles by the dimensions of their height and base rather than their hypotenuse and base, but it’s all part of the SAME triangle and the SAME proportional relationships.
The ratio of the hypotenuse of the Great Pyramid to its half base is the Golden Ratio, Phi, 1.618. It’s not “tenuous.” It’s exact to within 0.025%.
It’s a very elegant geometry that captures the unique relationship of “1 + Phi = Phi squared” in the “a squared + b squared = c squared” relationship of a Pythagorean right triangle. The sides of that triangle are 1, square root of Phi and Phi.
Geez, Gary, A hypotenuse is simply not the same as a side. The Golden Ratio is also called the Golden Rectangle,or the Golden Section. for a reason.
http://www2.rgu.ac.uk/subj/ats/TeachingWeb/teaching/t26-DesignPrinciples/TheGoldenSection/Parthenon.jpg
This triangle s just too ad hoc. The Egyptians certainly didn’t use it to build a pyramid. They know they can’t be too steep – the early ones crumbled.
No, the Golden Ratio is not also called the Golden Rectangle. The Golden Ratio is defined by a LINE divided at the one unique point that results in the ratio of whole line to the larger segment being the same as the ratio of the larger segment to the smaller segment. The ratio of the larger line to the smaller line is the Golden Ratio. You can then use those two LINE segments to create a RECTANGLE, which is called a GOLDEN RECTANGLE. You can also use them to create a right TRIANGLE, which is called a GOLDEN TRIANGLE or Kepler Triangle. (Note that other Golden Triangles can be made with a base of 1 and two sides of Phi or a base of Phi and two sides of 1.)
Johannes Kepler wrote of the unique qualities of this Golden Triangle, which is why it is named after him. Nothing “ad hoc” about. It’s just as legitimate a geometric construction as the Golden Rectangle. If the Egyptians did not use it to build this pyramid, they somehow stumbled upon some other geometry that produced a Golden Triangle with a very high degree of precision. Your argument that this proportion was used because “they can’t be too steep and crumble” fails because they built pyramids with a variety of other angles that are all still standing. Somehow though, they selected this very unique proportion for their most magnificent pyramid. The mathematics and geometry of this are undeniable, and also very easy to reproduce. All you need is three sticks of equal size and you can create a golden ratio. No knowledge of irrational numbers is required:
The TRUTH is that no one knows what geometry was used to construction the Great Pyramid. We just have the evidence of its physical dimensions and can study known methods of pyramid construction to come to reasonable conclusions.
The Great Pyramid of Giza is fact that our recorded history has been altered in that Eratosthenes was either one of three conclusions in being the first to accurately measure the circumference of the Earth. 1. He was the creator of the Pyramid of Giza, which would place him back further in time . 2. He is a recreation of the builder of the Great Pyramid of Giza, and is placed in history where he is today, hence hiding the Truths of the Great Pyramids overall reason for its construction that it was One of the Two points of reference used in accurately measuring the circumference of the Earth, for the foundation of Geography and Geodesy leading to the navigation of The world by the messiah son of the true bloodline of the written biblical kingdoms upon the Earth, in which the other point of reference is ‘Jacobs’ well of the jawbone in Israel or should I say ‘Eratosthenes ‘ well ? 3 He has stolen the Great Pyramids builders method , measurements etc…through his authority position of the Great library , erasing the true identity of the builder, for the purpose of maintaining the trinity tree of power for the elite pyramid money flow deceivers, that are the secret one world order biblical prophecy keepers of his mentor ‘ Plato ‘.