The Golden Ratios of the Parthenon

The Parthenon has long been associated with the golden ratio. The lack of clear evidence to support this though has led some to conclude in error that this is just a myth. This article will provide the best evidence I’ve found to date to illustrate appearances of golden ratios in the design of the Parthenon.

In my analysis, I’ll use the golden ratio grids created with pixel-level accuracy by my PhiMatrix software. These include golden rectangles and/or rectangles with a dividing line at the golden ratio point of their height or width. I’ll apply these to the best photos and illustrations of the Parthenon available. This requires that the images be very high resolution, and taken from directly perpendicular to the Parthenon to avoid distortions from perspective.

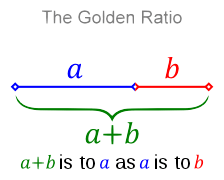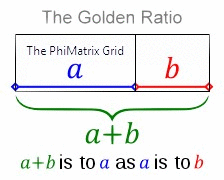
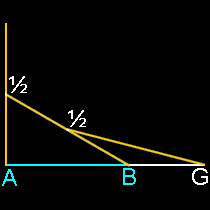
As a quick background, the golden ratio is defined by dividing a line at the one point at which the ratio of the larger segment (a) to the small segment (b) is equal to the ratio of the line (a+b) to the larger segment (a). Note that the PhiMatrix grid always shows the golden ratio point of any dimension:

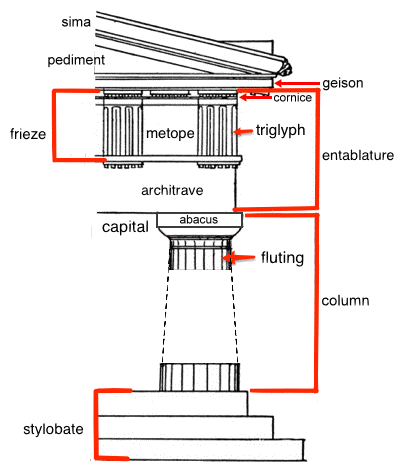
It will help to be familiar with names of the elements of classic Greek Doric architecture as well:

Golden ratios in the entablature of the Parthenon

One of the simplest constructions of the golden ratio is below. It divides a square at its midpoint and then with an arc creates a golden rectangle with the following properties:

• The height of the rectangle is the golden ratio of its width
• The width of the square is at the golden ratio point of the rectangle’s width
• The small vertical rectangle adjacent to the square is also a golden rectangle.

We find that this basic construction of a golden rectangle divided at its golden ratio point is found in the 14 golden rectangles formed by each metope and triglyph set across the frieze of the Parthenon:

• 

• 

• 

Note that even small variations from the golden ratio of 1.618… do not align well with the actual dimensions:

The architrave then was then designed to have the same height as the frieze. By doubling its height, this creates a golden rectangle with twice the dimensions of that of the frieze. This is used to create yet another golden ratio in the design:

• The distance between the columns is a golden ratio of the height of the entablature: 

• 

• 

A row of smaller blocks was set across the entire entablature to create the geison, which adds these golden ratio properties:

• Each block of the geison is a golden rectangle whose width is half that of the metope-triglyph golden rectangle.
• Each block of the geison has a horizontal dividing line at the golden ratio of its height.
• The height of the entablature with the geison added creates a golden rectangle that defines the width of the capital of the column.

• 

• 

• 

Golden ratios of the columns

The spacing of the columns and the width of the capitals of each creates yet another golden ratio property:

• The width of two capitals on the columns defines a golden rectangle whose height is that of the columns:

Golden ratios of the overall façade

This dimensions and proportions of the entablature and columns tie into an overall structure of design that creates the following golden ratios:

• The height of the Parthenon, from the base of the second step to the top of its roof peak (projected lines), is a golden ratio to its width at the end of the entablature.
• The base the entablature is at the golden ratio point of the height of the Parthenon.
• The top of the frieze is at the golden ratio point of the distance from the base of the architrave to the Parthenon’s height.

• 

For full disclosure and transparency:

• A bit of creative license must be taken in defining the base of the Parthenon. This is due to the fact that the base is in fact slightly curved, perhaps for drainage and also to make it look more perfect to the eye.
• The peak of the Parthenon must also be estimated based on the existing roof lines, as much of the pediment at the top was destroyed.
• The golden rectangle based on the width of two column capitals to the height of the columns is a more precise golden rectangle on the west façade than on the east façade.

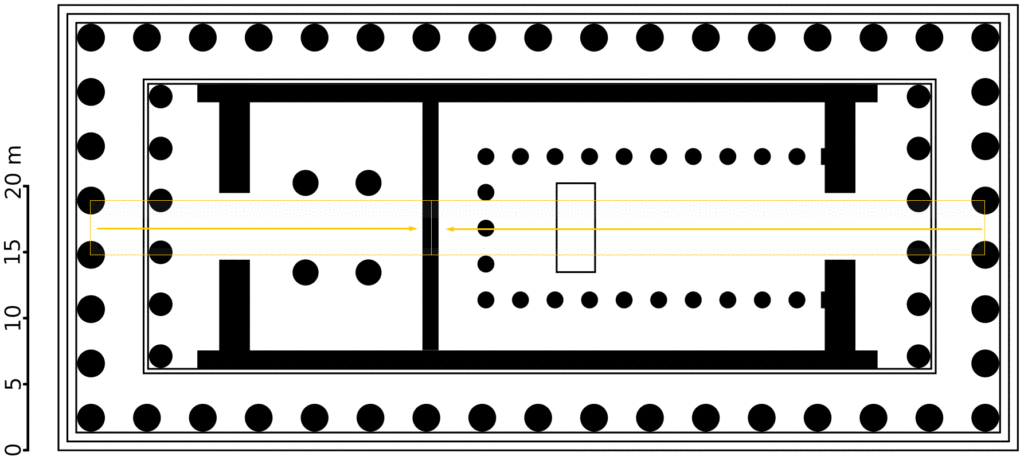
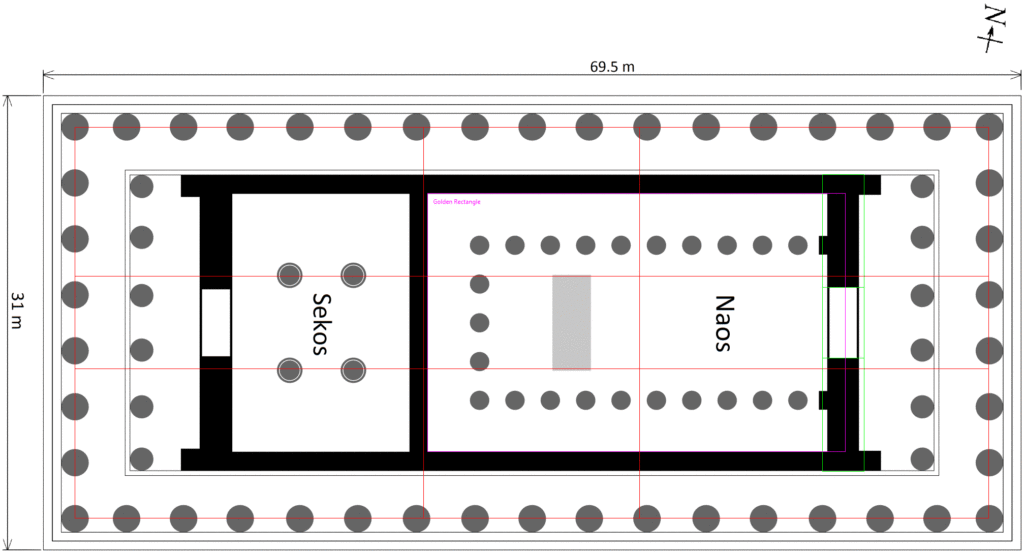
Golden ratios in the floor plan of the Parthenon

In addition to the golden ratios in its façade, there are also golden ratios that appear in the floor plan of the Parthenon:

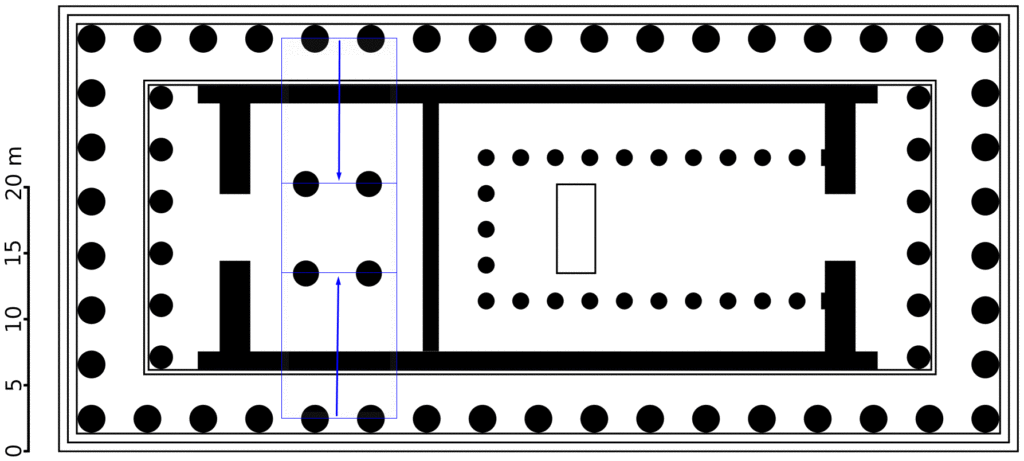
• The interior wall between the two chambers is at the golden ratio point of the distance between the center points of the exterior columns on each end.
• The centers of the interior columns and base of the statue of Athena are at the golden ratio points of the distance between the center points of the exterior columns on each side.
• The width of the entry way to the large chamber is a golden ratio of the distance between the outside of the outer walls of the interior chamber.
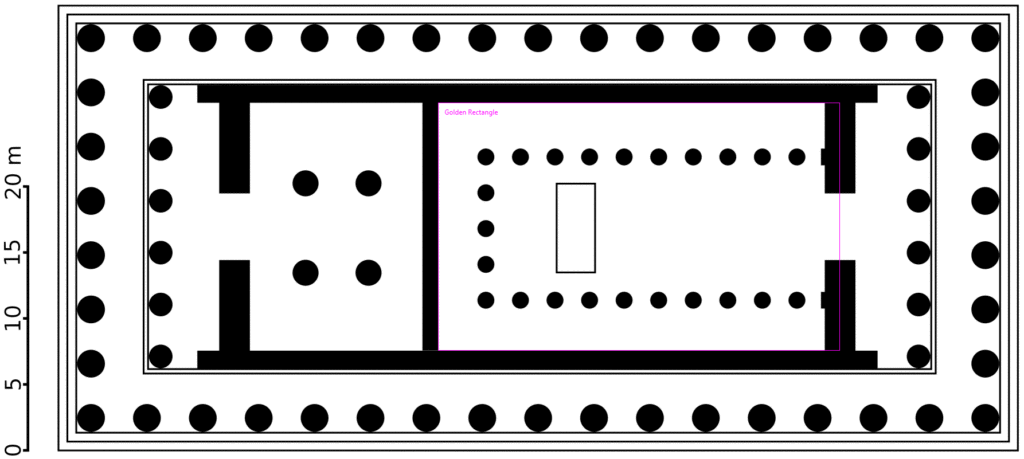
• The interior of the large chamber is a golden rectangle, when using the center of the entry wall as the rectangle’s perimeter.

• 

• 

• 

• 

• 

Source of original floor plan: Argento, public domain on Wikimedia.org.

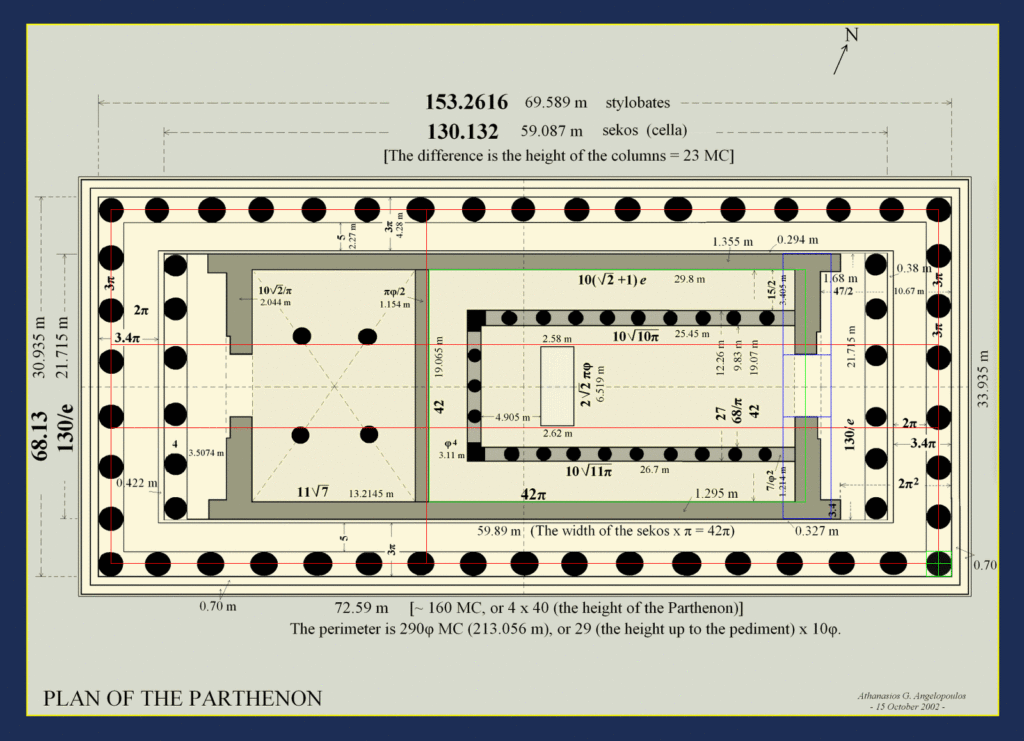
For transparency, note that a variety of Parthenon floor plans are available on the Internet, and they are not all consistent in their representations of dimensions. The above image was of very high resolution and includes a scale of the dimensions. Below are two other versions on which the golden ratios shown on the individual floor plans above are consolidated into a single view. Certain golden ratios align rather precisely across all three floor plans, including:

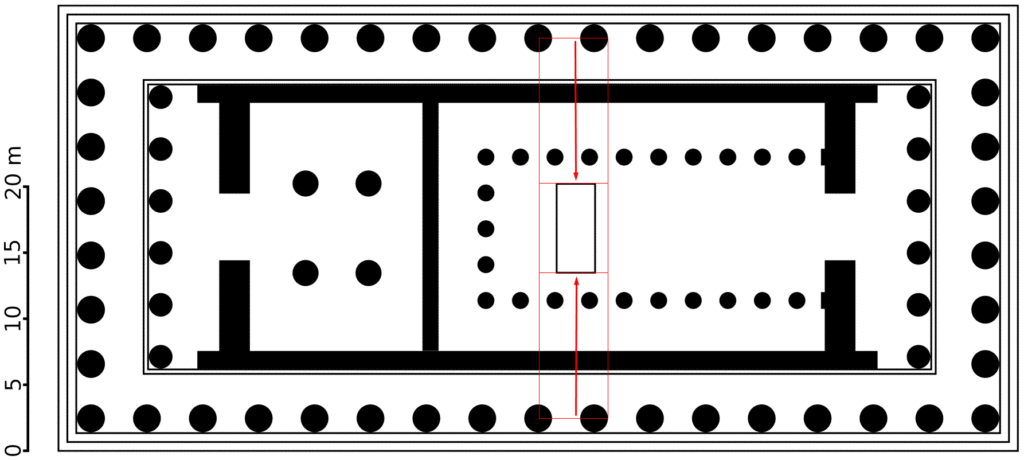
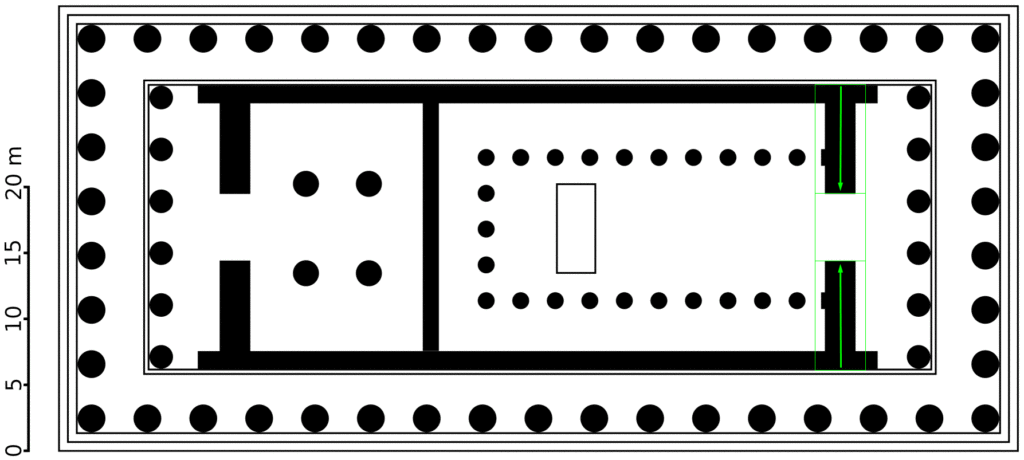
• The width of the entry way into the main chamber in relation to the width of the building
• The golden rectangle created by interior dimensions of the main chamber

Other dimensions vary slightly among the three floor plan versions, creating slight deviations from the golden ratios identified above:

• The exact position of the wall between the two interior chambers
• The exact positions of the four columns in the small interior chamber

Clearly only one version can be right, so I’ll gladly update this analysis for any source that can be shown to be authoritative and accurate.

• 

• 

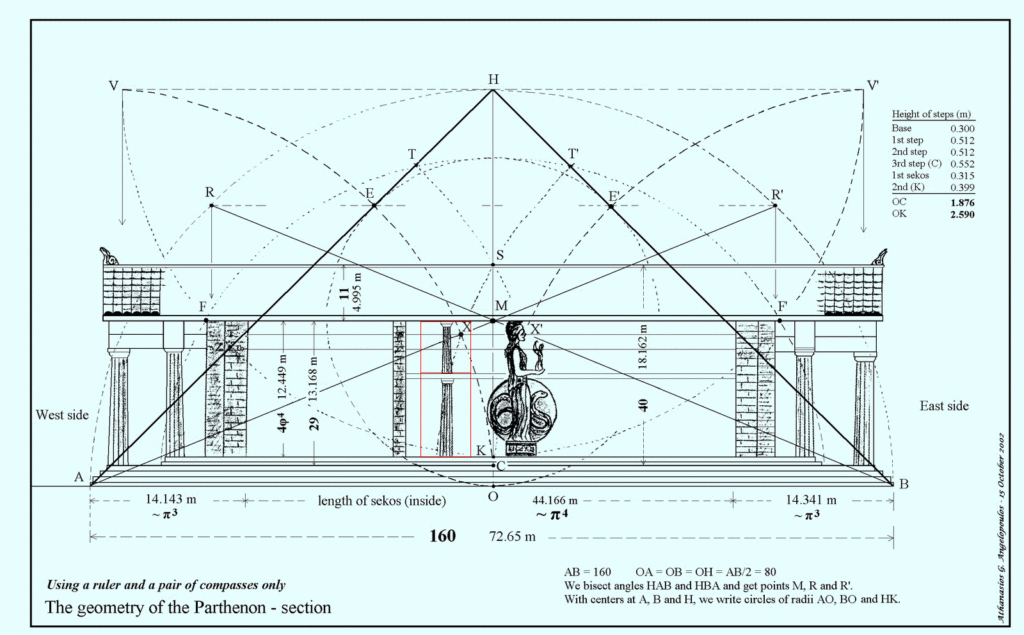
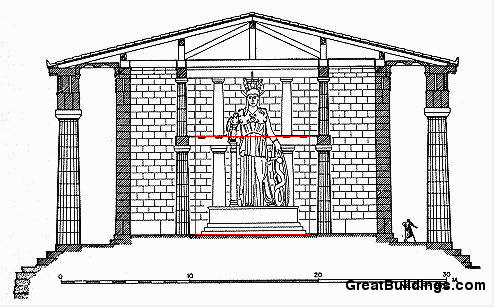
Golden ratios in the interior chamber

In addition to the golden ratios in the floor plan of the interior chamber, the interior chamber has two stacked sets of columns that appear to be in golden ratio proportion to each other.

• 

• 

Note here too that a variety of Parthenon interior illustrations are available which are not all consistent in their representations of dimensions. The Metron Ariston version was chosen because it is a well recognized source of Parthenon dimensions and of high resolution.

Support for application of the Golden Ratio by the Greeks

Beyond the physical evidence, followers of Pythagoras were using the golden ratio-filled pentagram as their secret symbol around 500 BC.

Polykleitos wrote “The Canon” around 450 BC, his treatise on aesthetic theories of the mathematical bases of artistic perfection.

The first known recorded references to the golden ratio did not appear until about 350 BC, when Euclid’s included numerous geometric constructions in his treatise Elements. According to Britannica though:

Euclid compiled his Elements from a number of works of earlier men. Among these are Hippocrates of Chios (flourished c. 440 BCE), not to be confused with the physician Hippocrates of Cos (c. 460–375 BCE). The latest compiler before Euclid was Theudius, whose textbook was used in the Academy and was probably the one used by Aristotle (384–322 BCE).”

Hippocrates thus compiled the first known work on the elements of geometry nearly a century before Euclid, right around the time when Polykleitos wrote on the mathematical basis of artistic perfection and when the Parthenon was being constructed between 447 and 432 BC.

Other research

For other background on this topic, please see the evidence for golden ratios in the design of the Parthenon and other historical information and perspectives in my previous writings over the years:

• My article “Phi and the Golden Section in Architecture,” published in 2003, as recorded on Archive.org.
• My article “The Parthenon and Phi, the Golden Ratio,” published on this site in 2013.
• My article “Dr. George Markowsky’s “Misconceptions about the Golden Ratio” Reviewed,” published on this site in 2016.
• My book “The Golden Ratio – The Divine Beauty of Mathematics,” published by The Quarto Group in 2018. See pages 104-108.
• My article “Donald Duck visits the Parthenon in ‘Mathmagic Land,” published on this site in 2020.
• My article “The Parthenon and the Golden Ratio: Myth or Misinformation?,” published on this site in 2020.

 An open invitation for research and collaboration

Research on the Parthenon is difficult because there are so many sources of information that are not consistent, and not well documented as to the authority or accuracy of the sources. Perhaps some of the best documentation is only available in Greek or in academic circles, which limits its availability. I welcome the opportunity to share and discuss findings with anyone on this topic, and can be reached through the Contact page of this website.

Credits:

Image of Parthenon East face used for analysis: Greece, Athen, Acropolis, Parthenon, from east, Date 9 October 2017, Author Berthold Werner, 6016×4000 pixels. This file is licensed under the Creative Commons Attribution-Share Alike 3.0 Unported license.

Image of Parthenon West face used for analysis: Western facade of the Parthenon during its restoration, Acropolis of Athens, Greece. Date, 20 July 2008, 2000×1579 pixels. Taken by Eusebius (Guillaume Piolle). Attribution: © Guillaume Piolle / CC BY 3.0

Interior view of Parthenon: Metron Ariston, a book written in 2002 and published on 11 February 2003 in Athens,Greece (275 pages – in Greek). ISBN 960-8286-06-9.

Interior view of Parthenon: GreatBuildings.com