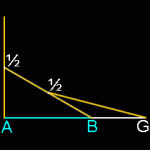
Phi (Φ) was described by Johannes Kepler as one of the "two great treasures of geometry." (The other is the Theorem of Pythagoras.) Phi appears in many basic geometric constructions. 3 lines: Take 3 equal lines. Lay the 2nd line against the midpoint of the 1st. Lay the 3rd line against the midpoint of the 2nd. The ratio of AG to AB is Phi, the Golden Ratio. (Contributed by … [Read more...]
Phi (the Golden Ratio) appears in a number of very interesting geometric constructions. It appears in basic constructions of triangles and squares within a circle, the pentagon. It also defines every point in 3D space in classic solids such as the dodecahedron, icosahedron and Bucky Ball. Johannes Kepler, who first discovered the beautiful elliptical nature of the orbits of the planets in our solar system described it as "a precious jewel" of geometry.
Spirals and the Golden Ratio
Fibonacci numbers and Phi are related to spiral growth in nature. If you sum the squares of any series of Fibonacci numbers, they will equal the last Fibonacci number used in the series times the next Fibonacci number. This property results in the Fibonacci spiral, based on the following progression and properties of the Fibonacci series: 12 + 12 + 22 + 32 + 52 = 5 x 8 12 + … [Read more...]
Phi Mandalas
Phi-based geometric shapes produce interesting mandala designs. A mandala is a geometric design, often symbolic of the universe and used in Eastern religions as an aid to meditation. Phi-based geometric shapes can be used to create some interesting phi mandalas, embodying the phi proportion found throughout creation and iterating into the infinitely large and the infinitely … [Read more...]
Penrose Tiling and Phi
Tiling in 5-fold symmetry was thought impossible! Areas can be filled completely and symmetrically with tiles of 3, 4 and 6 sides, but it was long believed that it was impossible to fill an area with 5-fold symmetry, as shown below: 3 sides 4 sides 5 sides leaves gaps 6 sides The solution was found in Phi, the Golden … [Read more...]
Squaring the Circle with Phi
Squaring the Circle comes within four decimal places using the Golden Ratio. Even before the foundations of the Great Pyramids were laid men have tried to "square the circle." That is, in a finite number of steps, construct a square and a circle that are precisely equal in area using only the most primitive instruments; namely, an unmarked compass & straightedge. Some of … [Read more...]
The DOR
A new fundamental geometric shape with a relationship to Phi. Here's a challenge to "all the real mathematicians in the back row," as my college professor often said: Picture the classic solids of geometry, each sitting inside a cube that encloses it on all sides. What is the ratio of surface area of this tangent cube to the surface area of the solid, and which solid … [Read more...]
Phi Formula Geometric Construction
Phi is most often calculated using by taking the square root of 5 plus 1 and divided the sum by 2: √5 + 1 2 This mathematical expression can be expressed geometrically as shown below: Three circle construction: Put three circles with a diameter of 1 (AB and DE) side by side and construct a triangle that connects the bottoms of the outside circles (AC) and the top and … [Read more...]
Quasi-crystals and the Golden Ratio
Quasi-crystals represent a newly discovered state of matter. Most crystals in nature, such as those in sugar, salt or diamonds, are symmetrical and all have the same orientation throughout the entire crystal. Quasicrystals represent a new state of matter that was not expected to be found, with some properties of crystals and others of non-crystalline matter, such as … [Read more...]
Orthogons and the Golden Auron
The Golden Section is an Orthogon called the Auron. The golden section can be constructed from a square with a compass and ruler: This is the most commonly known of twelve orthogons which can be constructed using this technique. Among orthogons, the golden section is known as the auron, coming from the root "aur," meaning gold. Orthogons provide a system of … [Read more...]
Phi and Fibonacci in Kepler and Golden Triangles
Creating a Triangle based on Phi (or Pythagoras meets Fibonacci): Pythagoras discovered that a right triangle with sides of length a and b and a hypotenuse of length c has the following relationship: a² + b² = c² A foundational equality of phi has a similar structure: 1 + Phi = Phi2 ( 1+ 1.618... = 2.618... ) By taking the square root of each term in this equality, we … [Read more...]