Abstract:
The application of the golden ratio by the designers of the Parthenon is a common point of confusion and dissension. Multiple seemingly credible sources state that the golden ratio was not used in the design of the Parthenon. Most of these, however, trace back to a single very inaccurate and incomplete article as their source. Once this information was published by a few recognized authorities, more people yet then quoted them as a “reputable” source, and the misinformation grew.
No disrespect is intended for those who have unknowingly created or passed along inaccurate or incomplete information. The objective here is to investigate the sources, examine the evidence, present the facts, and allow readers to have all information needed to come to their own evidence-based conclusions.
What the expert sources say
As of this writing in August 2020, Wikipedia’s article on the Parthenon says this:
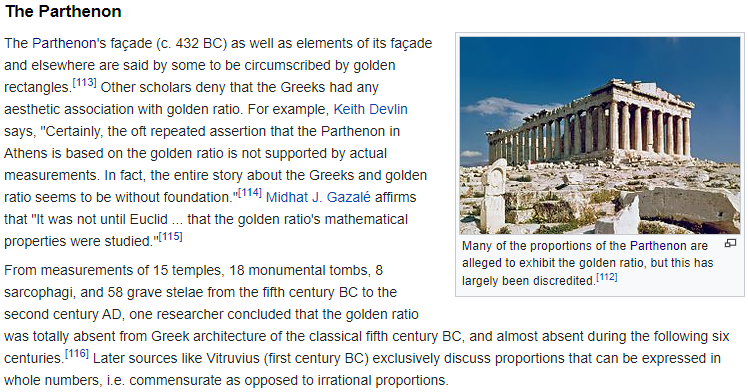
Some studies of the Acropolis, including of the Parthenon and its façade, have conjectured that many of its proportions approximate the golden ratio. However, such theories have been discredited by more recent studies, which have shown that the proportions of the Parthenon do not match the golden proportion. [66][67]“
Wikipedia’s article on the Golden Ratio says this:
Certainly, the oft repeated assertion that the Parthenon in Athens is based on the golden ratio is not supported by actual measurements. In fact, the entire story about the Greeks and golden ratio seems to be without foundation. [114]“
Checking the dissenting sources
Let’s look more closely at the references presented in the Wikipedia articles to understand the basis for their claims that the golden ratio’s appearance is unsupported and now discredited.
Dr. George Markowsky on the Parthenon
Reference 66 is to the 1992 article “Misconceptions about the Golden Ratio” by Dr. George Markowsky. I reviewed this article in 2016, and found that Dr. Markowksy had performed only a single relevant calculation of the Parthenon’s width to height. He referenced seven sources who claimed that the Parthenon did embody the golden ratio. He presented Figure 6 alone below to illustrate the claimed fit. Among his references are similar illustrations by David Bergamini in “Mathematics” and Theoni Pappas in “The Joy of Mathematics.”

Markowsky Parthenon illustration 

Bergamini – Mathematics 

Theoni Pappas – Joy of Mathematics
From the various sources, Dr. Markowsky calculated the ratio of the width of 101′ 3.75″ from Tractenberg and Hyman to the “height of the apex above the stylobate” of 59 feet from Rossiter. This yields a ratio of 1.717, which is not the golden ratio of 1.618…+. He references a quote by Christine Flon in “The World Atlas of Architecture“:
On the basis of a small number of ancient texts, an effort has been made to find (in buildings sufficiently well preserved) a coherent system of proportions based on the golden number, pi or on the universal ratios of the Pythagoreans. Almost always, when all possible measurements have been taken, some system of geometric figures or some modular common denominator has come to light. However, the validity of this research remains uncertain: it is easy to overestimate the importance of an architectural speculation, It is not unlikely that some architects, in imitation of sculptors such as Polycleitos, should have wished to base their works on a strict system of ratios, but it would be wrong to generalize. In the conservative environment of ancient Greece, architectural activity was an empirical practice in which experience and intuition, that is to say “mastery”, played a large part.”
I found the “World Atlas of Architecture” to be a wonderful resource on the history and style of architecture, but there is not one building in its 408 pages which references the mathematics of a building’s design. This is true even on its coverage of the UN Secretariat Building, whose architect, Le Corbusier publicly advanced his golden-ratio based system of design, called” Le Modulor”. So as good as this book is, it’s approach to the mathematics of design was to punt rather than to tackle the topic.
With Flon’s opinion on the “uncertain validity” and “speculation” in support of his finding though, Markowsky summarily dismissed the golden ratio of the Parthenon without any investigation into any of its other elements of design, and moved to the next topic in his article, which I review separately here.
In doing so, Markowsky notably omits the words of Flon that follow:
One thing is certain though: in the great civil and religious buildings there was a module, often the diameter of the column at its narrowest point— a basic dimension from which all the others were calculated. This made the designing and the dressing of the blocks easier, and permitted both the application and variation of proven formulae. In most cases the architect would not venture beyond simple arithmetic proportions which would ensure the uniformity of the building.”
Also of interest is that while Flon says that we should not generalize, she also notes that “it is not unlikely that some architects, in imitation of sculptors such as Polycleitos, should have wished to base their works on a strict system of ratios.“
Polykleitos wrote a treatise around 450 BC called “The Canon,” which comes from the Greek word kanon, meaning measure, rule, or law. It is a theoretical work that discusses ideal mathematical proportions for the parts of the human body, and aesthetic theories of the mathematical bases of artistic perfection. Though the text is lost to history, he is quoted as saying,
Perfection … comes about little by little (para mikron) through many numbers”.
According to the Getty Museum, references to “The Canon” in other ancient books:
imply that its main principle was expressed by the Greek words symmetria and rhythmos. By this Polykleitos meant that the work should be composed of clearly definable parts, all related to one another through a system of ideal mathematical proportions and balance.”
Symmetria means ‘common measure’. The Greeks interpreted this word, as the harmony of the different parts of an object, the good proportions between its constituent parts. This is exactly what the closer examination of the Parthenon (below) reveals. Rhythmos refers to the proportions and patterns as an exploration of the nature of motion.
Polykleitas worked alongside other Athenian sculptors, including Phidias, who designed the status of Athena and others for the Parthenon. Work on the Parthenon began in 447 BC, so the impact of Polykleitos’ treatise on artistic perfection could very well have had a very timely and direct impact on the design on Parthenon, and not be subject to the “generalization” Flon made in reference to all Greek architecture.
Dr. Mario Livio on the Parthenon
Reference 67 that follows on Wikipedia is to pages 74-75 of Dr. Mario Livio’s 2003 book, “The Golden Ratio: The Story of PHI, the World’s Most Astonishing Number.” Dr. Livio references books by Adolph Zeising (“The Golden Section”) and Matila Ghyka (“The Golden Number“) that claim this golden rectangle, and yet another golden ratio, but he then turns to Dr. Markowsky’s article. Dr. Livio includes yet another single, simple illustration of the Parthenon bordered by a golden rectangle. He refers to the same width to height measurements and ratio as Markowsky. He too quotes Christine Flon, and thus concludes “this is far less certain than many books would like us to believe and is not particularly well supported by the actual dimensions of the Parthenon.” Again, none of the many other design elements of the Parthenon are illustrated or addressed.

Reference number 112 in the Wikipedia article on the Golden Ratio appears in the caption of the the photo of the Parthenon, but we find that the reference simply says “Livio 2003, pp. 74–75,” duplicating the reference 67 that has already been given.
Dr. Keith Devlin on the Parthenon
Reference number 114 in the Wikipedia article on the Parthenon is from page 54 of Dr. Keith Devlin’s book, “The Math Instinct.” In the copy I purchased, the reference to the Parthenon appears on page 108. There the text simply states anecdotally, “Certainly, the oft repeated assertion that the Parthenon in Athens is based on the golden ratio is not supported by actual measurements. In fact, the entire story about the Greeks and the golden ratio seems to be without foundation.” Dr. Devlin presents no discussion at all of any evidence. No illustrations of the Parthenon are presented. No measurements or anything else are offered to support this statement.
I did a Google search to find that Dr. Devlin revealed his source in two of his articles on the Mathematics Association of America site:
- “Good stories, pity they’re not true,” June 2004, where referring to the Parthenon, architects in general, Leonardo da Vinci and painters in general, he states, “there’s not a shred of evidence to support any of these claims, and good reason to believe they are completely false, as University of Maine mathematician George Markowsky pointed out in his article “Misconceptions About the Golden Ratio”, published in the College Mathematics Journal in January 1992.”
- “The Myth That Will Not Go Away,” May 2007, where he states, “Then I read an excellent article by the University of Maine mathematician George Markowsky, titled “Misconceptions about the golden ratio”, published in the College Mathematics Journal in January 1992. In his article, Markowsky subjected many of the common claims about the golden ratio to a fairly rigorous review, and found that quite a few of them come up decidedly short. Further evidence against many of the common claims you see made about the golden ratio were provided by writer Mario Livio in his 2002 book “The Golden Ratio: The Story of PHI, the World’s Most Astonishing Number.”
So it turns out that Devlin’s “two” sources were Markowsky and Livio, and Livio’s source was Markowsky. Unfortunately, as of this writing many other sources are now quoting this “evidence” and accept the conclusions of Markowsky, Devlin and Livio as credible and established.
Devlin is a noted author on mathematics and NPR’s “The Math Guy.” Livio is also an accomplished author on mathematics and science, and widely recognized astrophysicist. These gentlemen are highly intelligent, and accomplished and recognized in their fields. Their words have broad impact, even if in this particular situation their positions were lacking in evidence and analysis.
In the end, none of these very recognized sources who stated that the golden ratios are not supported by the measurements did anything to go beyond a very simplistic and superficial calculation of the Parthenon’s width to height, and even this was done inaccurately. This lack of evidence and analysis presented to support their statements is indeed unfortunate.
Flaws in the Markowsky analysis
Before we examine what the evidence actually shows for golden ratios in the design of the Parthenon, we should understand this: If the golden ratio DOES exist, why did Dr. Markowsky not find it? The answer is surprisingly simple.
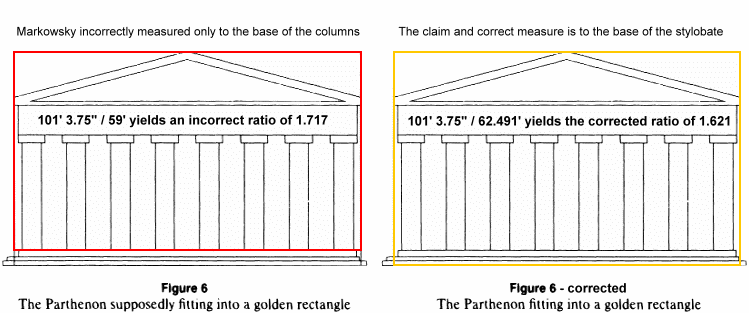
Note that Markowsky’s height measurement of 59 feet is based on “height of the apex above the stylobate.” This means that he measured from the base of the columns.
Note too that in ALL of the Parthenon illustrations presented, including Markowsky’s, that the golden rectangle is NOT based on the base of the columns “above the stylobyte.” Rather, the base of the golden rectangle INCLUDES the steps of the stylobyte that lead up to the Parthenon.”
Let’s determine what his results would have been if his measurements had been consistent with the supporting illustrations.


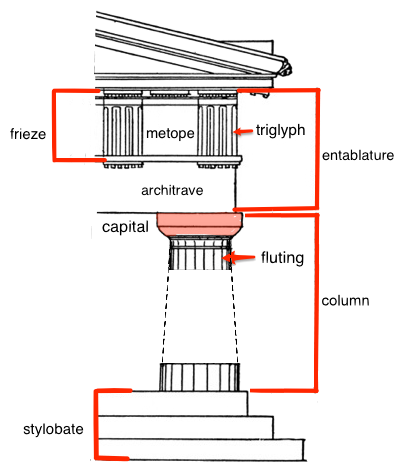
Classic architecture terms 


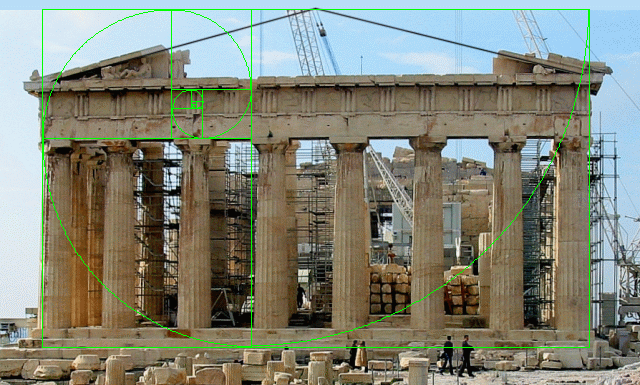
Markowsky Parthenon illustration 

Markowsky illustration overlayed to actual Parthenon Photo 

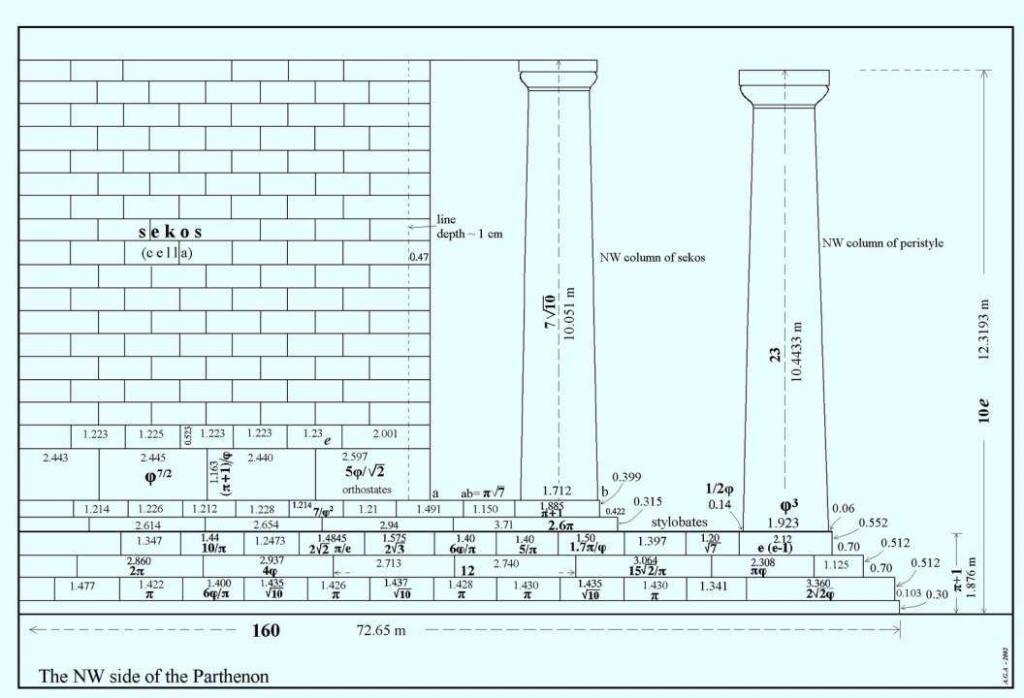
Source: Metron Ariston, 2002
According to the book Metron Ariston (2002), the height of the first two steps descending from the stylobyte are 1.811 feet and 1.680 feet, respectively. If we add that to the height included in the Parthenon’s height, we get 62.491 feet instead of 59 feet.
The ratio of the width of 101′ 3.75″ to revised height of 62.491′ is 1.621, a variance of only 0.20% from the golden ratio of 1.618 (to four digits)! This is well within the tolerance that Dr. Markowsky established for the basis of his investigation and conclusions.

It makes perfect sense too that any measure of the Parthenon’s height to width should include its stylobye/base, for this is critical to what the observers sees as “The Parthenon.” If asked to draw the Parthenon, anyone with good observational skills would draw the structure with its base foundation, not just columns on the ground.
More importantly, if Dr. Markowsky had expanded his investigation beyond a very simplistic measure of height vs. width, he likely would have found a much richer body of evidence for appearances of the golden ratio in the Parthenon, just as did Donald Duck in the 1959 film, “Donald in Mathmagic Land.” Both Devlin and Livio would have been quoting different evidence, measurements and conclusions as well, as would be the many who have since quoted them.
Curiously Dr. Markowsky, in his March 2005 review of Dr. Livio’s Golden Ratio book, acknowledges being exposed to the golden ratio in “a comic book entitled Donald in Mathmagic Land, which later became an animated cartoon.” In his defense, the comic book unfortunately didn’t show the same level of detail in the golden ratios of the Parthenon that are presented in Disney’s animated film by the same name. One can’t help but wonder if his evidence and conclusions might have been different if he’d seen the film.
What the evidence shows
I’ve presented evidence for golden ratios in the design of the Parthenon in several of my writings over the years:
- My article “Phi and the Golden Section in Architecture,” published in 2003, as recorded on Archive.org.
- My article “The Parthenon and Phi, the Golden Ratio,” published on this site in 2013.
- My article “Dr. George Markowsky’s “Misconceptions about the Golden Ratio” Reviewed,” published on this site in 2016.
- My book “The Golden Ratio – The Divine Beauty of Mathematics,” published by The Quarto Group in 2018. See pages 104-108.
- My article “Donald Duck visits the Parthenon in ‘Mathmagic Land,” published on this site in 2020.
- My article “The Golden Ratios of the Parthenon,” published on this site in 2020.
Note that “The Golden section in architecture – The Parthenon and Greek Architecture,” published by Dr. Ron Knott (PhD, Mathematics) in 1999 also showed the some of the same basic golden ratios.


You can find more detailed high resolution image analyses on the pages listed above, but many of the most apparent golden ratios identified in the proportions of the Parthenon are illustrated in these images. The golden rectangles and golden ratio divisions on these images were created with pixel-level accuracy using my PhiMatrix software.
Parthenon Golden Ratio Summary
So between Disney’s “Donald in Mathmagic Land” and my articles listed above, we find evidence that appears to substantiate the application of golden ratios in the following design elements of the Parthenon:
Façade:
- Façade – Overall height vs width, if you accept starting from the second step. Using that approach, there is then another golden ratio from the bottom of the second step to the top of the columns to the top of the roof.
- Triglyph – Rectangles formed by the Triglyphs.
- Metope/Triglyph – Rectangles formed by each pair of Metopes and Triglyphs.
- Entablature/Architrave – Height of the Entablature to the height of the Architrave.
- Frieze/Roofline – Height from the Column top to the top of the Frieze to the height of the roof top.
- Capitals/Entablature – Width of each pair of column Capitals in relation to the height of the Entablature.
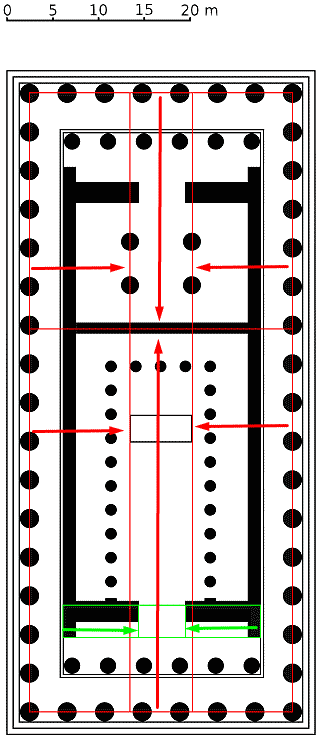
Floor Plan:
- Perimeter Outside Columns/Chamber wall – Center points of the exterior columns in relation to the position of the wall between the two interior chambers.
- Perimeter Columns/Inner columns – Center points of the exterior columns in relation to the centers of the four columns in the smaller interior room.
- Building width/Entry width – Width of the inner enclosed structure of the Parthenon in relation to the width of the entry way into the large interior chamber.
Even if you don’t accept every single appearance presented above as a golden ratio, it would be inaccurate to say that “no evidence exists” or that this is a story “without foundation.” It would also not be reasonable to assume that these appearances were all due to coincidence, without any awareness or intent by the designers.
A geometric perspective
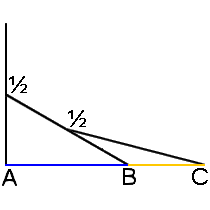
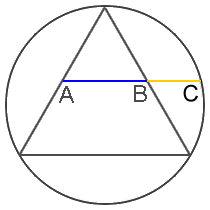
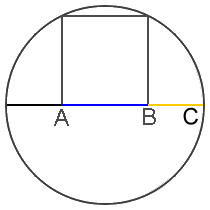
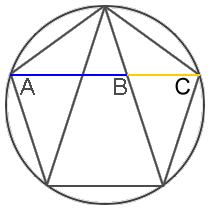
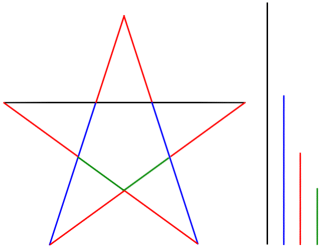
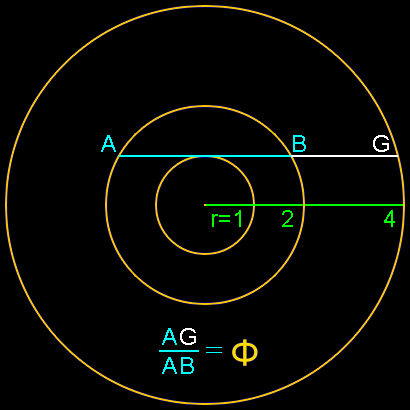
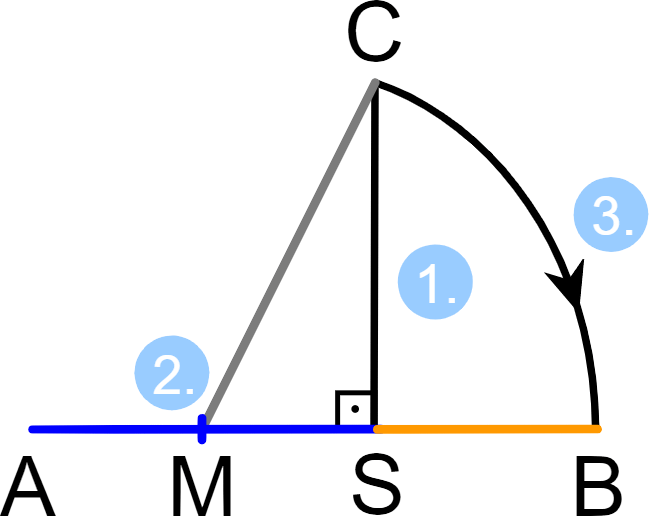
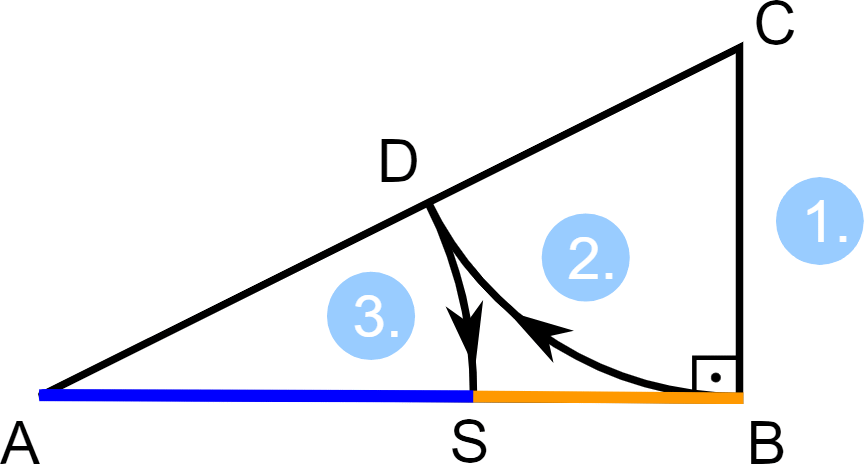
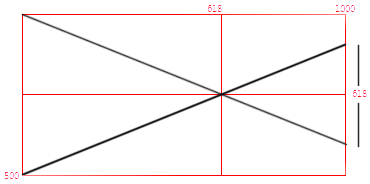
Frankly, we should be more surprised if the golden ratio did NOT appear among the Parthenon’s numerous precise mathematical proportions. It is truly one of the easiest ratios to create with simple geometric constructions, and likely the most ubiquitous ratio in mathematics, geometry and nature. The constructions below illustrate illustrate this fact:
Interestingly, one of the simplest geometric constructions of the golden ratio appears to be applied and illustrated in design of the frieze. It appears fourteen times actually, so it’s hard to miss:




The Greeks were clearly very intentional and precise in the numbers and proportions they incorporated into the Parthenon’s design. If the golden ratio were not used, a more compelling argument to support this premise would require developing a theory for what the Greeks DID in fact use, rather than to simply say that no evidence exists. The analysis in the photo below shows that other simple integer ratios like 3:2 and 5:3 do not match the proportions used in the frieze, but the golden ratio does:


An application perspective
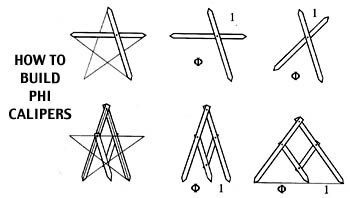
Once a golden ratio has been determined with a simple geometric construction, replicating it for application in the arts is even simpler yet. All that is required is two sticks or rods of equal length that are attached at their golden ratio point. This then creates a measuring divider that can identify the golden ratio of any dimension in a second or two. Dividers have been in common use in construction since the time of the Greeks and Romans.
A historical perspective
Beyond the physical evidence itself, history tells us that followers of Pythagoras were using the golden ratio-filled pentagram as their secret symbol around 500 BC.
In about 450 BC, Polykleitos wrote “The Canon,” his treatise on aesthetic theories of the mathematical bases of artistic perfection.
It wasn’t until 300 BC that Euclid had written the first known recorded references to the golden ratio in numerous geometric constructions in his treatise Elements, but according to Britannica:
Euclid compiled his Elements from a number of works of earlier men. Among these are Hippocrates of Chios (flourished c. 440 BCE), not to be confused with the physician Hippocrates of Cos (c. 460–375 BCE). The latest compiler before Euclid was Theudius, whose textbook was used in the Academy and was probably the one used by Aristotle (384–322 BCE).”
Hippocrates thus compiled the first known work on the elements of geometry nearly a century before Euclid, right around the time when Polykleitos wrote on the mathematical basis of artistic perfection and when the Parthenon was being constructed between 447 and 432 BC.
So it’s reasonable to assume that knowledge of the golden ratio could have existed when the Parthenon was designed and built.
A forensic analysis perspective
For those who like TV crime shows, you may know that there are three elements of evidence often required to establish that a crime has been committed. While applying the golden ratio to the Parthenon would certainly not be a crime, we can use a forensic analysis approach to assess whether there is a case for its use. The three elements of evidence are:
- Motive – Having a reason to commit the act.
- Means – Having the tools or methods to commit act, and
- Opportunity – Having the occasion present itself to allow the act to take place.
For someone to become a suspect in a criminal investigation, all three must be established.
So in the case of the Parthenon, we know the Greeks valued incorporating mathematics and geometry into their art and architecture (motive). We know that the pentagram with its golden ratio proportions was recognized and revered for its special properties at least one hundred years before the construction of the Parthenon, and that this evolved into a very sophisticated set of constructions and propositions in Euclid’s Elements by one hundred years after (means). We know that the Parthenon, as the pinnacle of Greek architecture, would have presented a wonderful opportunity to apply the golden ratio in its design (opportunity).
Myth or Misinformation?
So hopefully you now have enough evidence and information to decide for yourself:
Does it seem most likely that the Greeks applied the golden ratio in the design of the Parthenon, or is this just a myth that won’t go away?
I look forward to your comments below.
Update on new research
Note: See an update with my latest research on the Parthenon here:
- My article “The Golden Ratios of the Parthenon,” published on this site in October 2020.













I think that one could look at just about any building on earth and find some aspects of it the conform (almost) to the golden ratio. This does not in any way mean that the ratio was used in its design, it simply means that some elements are in a ratio between 1.5: to 1 and 1.7 to 1. It’s simply a visually pleasing ratio that occurs by chance.
But no one would claim that a building with “some proportions” between 1.5 and 1.7 has therefore “conformed” to the golden ratio. We’re talking about a building which has nine of its most fundamental design features reflecting the golden ratio to at least 3, if not 4, places of accuracy.
To keep things simple and conservative, let’s just say six key elements of the Parthenon’s design reflect the golden ratio, accurate to 3 decimal places. There are 21 three-digit numbers from 1.5 to 1.7 (e.g., 1.50, 1.51, 1.52, etc.) If all we were trying to do is find proportions on a building between 1.50 and 1.70, we’d have a 1 in 21 chance of any proportion hitting 1.62 (the rounded golden ratio). For six primary design elements to come in at 1.62, however, the odds of that are 1 in 21 to the sixth power, or 1 in 85,766,121.
What basis in reason or mathematics is there for concluding that this “occurs by chance?” Doesn’t the evidence more reasonably lead to the conclusion that the architects were intentionally incorporating the golden ratio into the design, and not just randomly picking “visually pleasing” proportions between 1.5 and 1.7 as they went along?
I have been thinking of the about patterns in nature and the golden ratio for a long time. Your article addressing the controversy around the parthenon is appreciated. I am currently writing a book on the foundations of pattern in nature and I have tentatively abstracted some images of the parthenon from from your article. which I attribute to you. If and when this come to fruition, I of course would seek some formal approval
Of course Phidias had nothing do with the golden section that was described by Euclid a generation after the construction of the Parthenon. It was not named “golden” until some procrustean German named it “golden” in the 19th century. Phidias did not like straight lines and the Parthenon had no straight lines. How can you have a golden section defined on a curved line?
I called procrustean the naming of the a/b=b/(a+b) ratio golden, because it is trying to shoehorn beauty into math. Real artists do not paint by the number. It is the other way around they discover numbers through their art.
We shouldn’t be so quick to assume that Phidias had nothing to do with the golden ratio. Euclid compiled his Elements from a number of works of earlier men. Among these are Hippocrates of Chios (flourished c. 440 BCE). Phidias lived from 480 BC to 430 BC. Wikipedia reports that “is possible that most of sculptural decoration of the Parthenon was the work of Phidias’ workshop.” (https://en.wikipedia.org/wiki/Phidias)
It’s true that the Parthenon has “no straight lines,” but the curves are almost visually imperceptible and used only to improve the visual appearance of the structure. See my analysis at https://www.goldennumber.net/parthenon-golden-ratio-design/ and you’ll find plenty of examples of the golden ratio in its design. Furthermore, it’s actually quite easy to apply the golden ratio to a curved line. The “golden angle” that is the basis for the spirals that appear in plants is determined by taking a 360 degree circle and dividing it by the golden ratio to get two arcs of 137.5 degrees and 225.50 degrees.
Re “real artists do not paint by the number,” Kenneth Clark, author of “Civilisation” observed “This union of art and mathematics is far from our own way of thinking, but it was fundamental to the Renaissance.”
Pythagoras, about 50 years before construction of the Parthenon, invented the framework of ancient Greek geometry, when the Pythagoreans discovered the existence of irrational numbers and wanted to study them. The symbol of the Pythagoreans was the regular pentagram, a geometric figure that embodies the Golden Ratio like no other. His teachings were the likely source for Euclid’s Elements books I and II, Book II being titled “The Theory of Rectangles”., which has several instances of the Golden Ratio, starting with Proposition XI, where Euclid presents a construction of the Golden Rectangle.
There was a huge rift the ancient mathematics of Greece as this time, where the conservative side rejected the notion of irrational numbers and stuck to using rational numbers and arithmetic, and on the progressive side were those that embraced the new invention of geometry, which operated with continuous proportions and irrational numbers. This argument is reflected in the source material you quoted from Flon.
I would suspect that the progressive geometers won out over the conservative arithmeticians on the design of the Parthenon, intended to be the grandest building building in Athens.
Have you thought about writing a full rebuttal to Dr. Markowsky’s 1992 article “Misconceptions about the Gold Ratio”, which seems to be the often cited source of the cynicism about the use of the Golden Ratio in ancient architecture?
I feel like his attack on the Kepler Golden Triangle in the design of the the Great Pyramid was very dismissive of the ancient Egyptian’s abilities as mathematicians. Unfortunately, we do not have the blueprints that they used (as papyrus tends to disintegrate after a millenia or two) but a millennia after the pyramid was built, we know of the Rhind Papyrus, which entailed mathematics useful for economics and tax collectors, including a fairly sophisticated approximation of pi that differed by only one percent, The Sumerians, only one river basin away from Egypt, and of the time period that is roughly contemporary with Khufu (circa 2600 BCE), we knew had methods of dealing with irrational numbers and calculating approximations for a positive root of quadratic equations, from a tablets dated to around 2000 BCE. (6 centuries after Khufu, 16 centuries before Pythagoras discovered irrational numbers, and over 20 centuries before Abu Kamil systematically solved quadratic equations using al-jabr)
We have evidence that the ancient Egyptians of Khufu’s time were excellent astronomers, which requires a deep understanding of mathematics. I would think that in building the world’s tallest building (that held on to that record for almost four millennia until the 14th century) would have been very special, and they would have put their best and brightest math nerds on it.
Great points, and I agree with all of them.
I wrote a full rebuttal in 2016 to Dr. Markowsky’s 1992 article here:
https://www.goldennumber.net/golden-ratio-misconceptions-by-george-markowsky-reviewed/
I don’t doubt that he had good intent, and give him credit for putting more thought into his article than the critics who just claim “No evidence exists!” Unfortunately, the article was biased, very poorly researched and had many flawed assumptions and conclusions.
More unfortunately yet, so many people, most notably academics, have quoted the article without applying a bit of critical thinking or analysis to it. Isn’t peer review supposed to be the hallmark of academic research that assures the quality of academic literature?