What makes a single number so interesting that ancient Greeks, Renaissance artists, a 17th century astronomer and a 21st century novelist all would write about it? It’s a number that goes by many names. This “golden” number, 1.61803399, represented by the Greek letter Phi, is known as the Golden Ratio, Golden Number, Golden Proportion, Golden Mean, Golden Section, Divine Proportion and Divine Section. It was written about by Euclid in “Elements” around 300 B.C., by Luca Pacioli, a contemporary of Leonardo Da Vinci, in “De Divina Proportione” in 1509, by Johannes Kepler around 1600 and by Dan Brown in 2003 in his best selling novel, “The Da Vinci Code.” With the movie release of the “The Da Vinci Code”, the quest to know Phi was brought even more into the mainstream of pop culture. The allure of “The Da Vinci Code” was that it creatively integrated fiction with both fact and myth from art, history, theology and mathematics, leaving the reader never really knowing what was truth and what was not. This site studies this golden number Phi, and its mathematical cousin, the Fibonacci sequence (0, 1, 1, 2, 3, 5, 8, …) , both of which have roles in the plot of this murder mystery, and distinguishes between the myth and the math.
| (Phi-based grid lines created with PhiMatrix golden ratio software) |
Mathematics of the Golden Ratio
This Golden Ratio truly is unique in its mathematical properties and pervasive in its appearance throughout nature. The “mathematically challenged” may be more interested in the appearances of Phi in nature, its application to art, architecture and design, and its potential for insights into the more spiritual aspects of life, but let’s begin with the purest of facts about Phi, which are found in mathematics.
Most everyone learned about the number Pi in school, but relatively few curricula included Phi, perhaps for the very reason that grasping all its manifestations often takes one beyond the academic into the realm of the spiritual just by the simple fact that Phi unveils a unusually frequent constant of design that applies to so many aspects of life. Both Pi and Phi are irrational numbers with an infinite number of digits after the decimal point, as indicated by “…”, the ellipsis.
Where Pi or p (3.14…) is the ratio of the circumference of a circle to its diameter, Phi or Φ (1.618 …) is the Golden Ratio that results when a line is divided in one very special and unique way. To illustrate, suppose you were asked to take a string and cut it. There’s any number of places that you could cut it, and each place would result in different ratios for the length of the small piece to the large piece, and of the large piece to the entire string. There is one unique point, however, at which the ratio of the large piece to the smaller piece is exactly the same as the ratio of the whole string to the larger piece, and at this point this Golden Ratio of both is 1.618 to 1, or Phi.
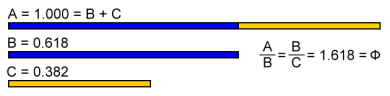
What makes this so much more than an interesting exercise in mathematics is that this proportion appears throughout creation and extensively in the human face and body. It’s found in the proportions of many other animals, in plants, in the solar system and even in the price and timing movements of stock markets and foreign currency exchange. Its appeal thus ranges from mathematicians to doctors to naturalists to artists to investors to mystics.
Part of the uniqueness of Phi is that it can be derived in many other ways than segmenting a line.
- Phi is the only number whose square is greater than itself by one, expressed mathematically as Φ² = Φ + 1 = 2.618.
- Phi is also the only number whose reciprocal is less than itself by one, expressed as 1/Φ = Φ – 1 = 0.618.
These two qualities of phi can be expressed algebraically as a+1=a² and a-1=1/a. This can then be rearranged and expressed as a²-a -1=0 . This is a quadratic equation, the only positive solution of which is:
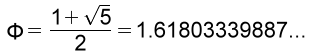
Φ = (1 + √5) /2 = 1.61803398874989484820…
Where 1.618 is represented in upper case as Phi or Φ, its near twin or reciprocal, 0.618, is often represented in lower case as phi or φ. Phi is an irrational number, a number which cannot be expressed as a ratio of two integer numbers.
The Fibonacci Sequence
The Fibonacci sequence, also a plot element in “The Da Vinci Code,” provides yet another way to derive Phi mathematically. The series is quite simple. Start with 0 and add 1 to get 1. Then repeat the process of adding each two numbers in the series to determine the next one: 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, and so on. This pattern is also found in the diagonals of Pascal’s Triangle. The relationship to the Golden Ratio or Phi is found by dividing each number by the one before it. The further you go in the series, the closer the result gets to Phi. For example:
1/1=1
2/1=2
3/2=1.5
5/3 = 1.666
13/8 = 1.625
21/13=1.615
If you go further into the series and you’ll find that 233/144 = 1.61805, a very close approximation of Phi, which to ten decimal places is 1.6180339887.
Geometry of the Golden Ratio
The Golden Ratio is also found in geometry, appearing in basic constructions of an equilateral triangle, square and pentagon placed inside a circle, as well as in more complex three-dimensional solids such as dodecahedrons, icosahedrons and “Bucky balls,” which were named for Buckminster Fuller and are the basis for the shapes of both Carbon 60 and soccer balls.
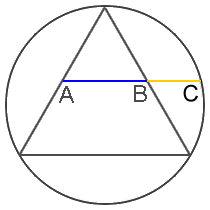
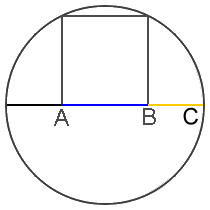
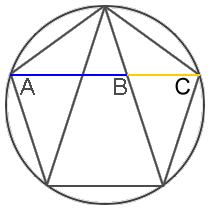
Johannes Kepler (1571-1630), discoverer of the true elliptical nature of the orbits of the planets in the solar system described it as such: “Geometry has two great treasures: one is the Theorem of Pythagoras; the other, the division of a line into extreme and mean ratio. The first we may compare to a measure of gold; the second we may name a precious jewel.” (See other Quotations)
Nature and Life
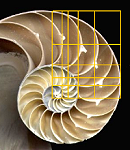
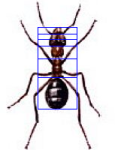
There are many other fascinating mathematical relationships and oddities in both Phi and the Fibonacci series that can be explored in more depth, but for now let’s now take a step away from the purely mathematical and venture into nature, where Phi and the Fibonacci series manifest themselves pervasively, but not universally. Fibonacci numbers frequently appear in the numbers of petals in a flower and in the spirals of plants. The positions and proportions of the key dimensions of many animals are based on Phi. Examples include the body sections of ants and other insects, the wing dimensions and location of eye-like spots on moths, the spirals of sea shells and the position of the dorsal fins on porpoises. Even the spirals of human DNA embody phi proportions.
Perceptions of Beauty
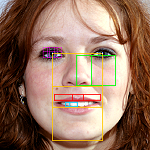
More intriguing yet is the extensive appearance of Phi throughout the human form, in the face, body, fingers, teeth and even our DNA, and the impact that this has on our perceptions of human beauty. Some would argue that beauty is in the eye of the beholder, but there is evidence to support that what we perceive as beauty in women and men is based on how closely the proportions of facial and body dimensions come to Phi. It seems that Phi is hard-wired into our consciousness as a guide to beauty. For this reason, Phi is applied in both facial plastic surgery and cosmetic dentistry as a guide to achieving the most natural and beautiful results in facial features and appearance.
Art, Architecture and Design
With all the unique mathematical properties of Phi and its appearance throughout creation, it’s little wonder that mankind would not only take notice of this number and the Golden Ratio it creates, but also use it to capture the beauty and harmony of nature in our own creations in art, architecture and other areas of design. In some cases, mankind’s application of Phi is undeniable. In other cases, it is still the subject of debate. The Great Pyramid of Egypt appears to embody the Golden Ratio in the ratios of its base, height and hypotenuse, but its missing outer shell and the absence of the mention of Phi in ancient Egyptian writings make it difficult to prove conclusively that this was by design. The Greeks knew of Phi at the time of the building of the Parthenon, and while its overall dimensions only approximate the golden ratio, there appears to be evidence of it use in the design of the beam atop the columns. The confusion on these points leads to those who contest this as well. It is recognized that Leonardo Da Vinci used Phi, known in the 1500’s as “The Divine Proportion,” in a number of his paintings. Other artists, including Raphael, Sandro Botticelli and Georges Seurat did as well. While this is undeniable, some people creatively overlay golden spirals to images where others do not believe they were intended by the artist. The dimensions of the treasured Stradivarius violins built around 1700 show Phi relationships. It plays a role in music and acoustics. More modern applications of the Golden Ratio in architecture can be seen in Notre Dame in Paris, the United Nations Headquarters Secretariat building in New York and the CN Tower in Toronto. It’s commonly used in the design of products and logos and by many major corporations. It has even been used in high fashion clothing design, such as in the “Phi Collection” announced in 2004 and covered by Vogue, Elle and Vanity Fair. It’s also the basis for The Fashion Code, a style guide to women’s dress. Various studies have tested to see if a golden rectangle is the most pleasing rectangle to the human eye. Results of the studies are mixed, but generally point to rectangles with shapes close to the golden rectangle as being most pleasing.
The Solar System and Universe
Curiously enough, we even find golden ratio relationships in the solar system and universe. The diameters of the Earth and Moon form a triangle whose dimensions are based on the mathematical characteristics of phi. The distances of the planets from the sun correlate surprisingly closely to exponential powers of Phi. The beautiful rings of Saturn are very close in dimension to the golden ratio of the planet’s diameter. NASA released findings in 2003 that the shape of the Universe is a dodecahedron based on Phi.
New Discoveries involving the Golden Ratio
The Golden Ratio continues to open new doors in our understanding of life and the universe. It appeared in Roger Penrose’s discovery in the 1970’s of “Penrose Tiles,” which allowed surfaces to be tiled in five-fold symmetry, a task previously thought impossible. It appeared again in the 1980’s in the three-dimensional molecular arrangement of quasi-crystals, a newly discovered form of matter. As we enter the 21st century, Phi seems to be having a rebirth in integrating knowledge across a wide variety of fields of study, including time and quantum physics.
Spiritual Aspects
The description of this golden proportion as the Divine proportion is perhaps fitting because it is seen by many as a door to a deeper understanding of beauty and spirituality in life, unveiling a hidden harmony or connectedness in so much of what we see. That’s an incredible role for a single number to play, but then again this one number has played an incredible role in human history and in the foundations of life itself. The line between its mathematical and mystical aspects is thus not easily drawn.
Phi does not appear explicitly in the Bible or other ancient scriptures, yet we find that the dimensions given by God to Noah for the Ark and to Moses for the Ark of the Covenant both reflect a 5 to 3 proportion, Fibonacci numbers with a ratio of 1.666, and a reasonably close approximation to Phi. The Kaaba, the most sacred site of Islam in Mecca, is located very close to the golden ratio of the distance between the Earth’s north and south poles. Curiously enough, even the symbol for Phi, a circle with a line drawn through it, can be thought to represent a zero, or void, divided by one, or Unity, to create beauty, analogous to God creating the universe from nothing.
A Journey of Discovery
In matters of reason, seeing is believing but in matters of faith, it is believing that first opens the door to seeing. Just as we need two eyes to add depth to our perception in vision, both faith and reason serve us in adding depth to our understanding of life and the universe in which we live. Some will tell you that appearances of the Golden Ratio are proof of God’s design. Most religions though reveal that we come to know God through faith, not proofs. Some will tell you that there isn’t even any evidence at all for the Golden Ratio, that we’re just perceiving patterns that don’t really exist. Probe further though to ask if their views are based in evidence, or just a reflection of their own atheistic or naturalistic beliefs about life.
The best way to know for yourself where Phi appears and where it is imagined is to explore with an open mind, learn and reach your own conclusions on the facts and implications. You can learn more about the Golden Ratio here at www.GoldenNumber.net and download a free trial of PhiMatrix golden ratio design software to easily discover and apply Phi proportions for yourself. Enjoy the “phi”nomemon, whether to enhance your own understanding and appreciation of beauty and harmony in life or to apply it to your own artistic creations, like Leonardo Da Vinci and other masters before you. I welcome you to contribute your own insights and findings with our online community.
Gary Meisner
The Phi Guy
Author of www.goldennumber.net
Developer of PhiMatrix software at www.phimatrix.com







math project
Im doing this as my project too!
i have this math project and it is about the golden ratio. I have to analyse celebrity faces and figure out what is their golden ratio then we have figure out which celebrity is closest to THE golden ratio. We also have to write a documentary about it and create a survey its due to tomorrow and i have not even started. PLEASE HELP !
I do not get my math project any suggestions on how to do it would be the most amazing thing at this moment. PLEASE HELP !
You’ve at least come to a good place to get started. See the articles at https://www.goldennumber.net/category/face-beauty/, and also the research of Dr. Stephen Marquardt at http://www.beautyanalysis.com.
Cool articles. Unfortunately, though, I think you responded too late to help that poor math student. It’s a lost cause…
I gave it a good try. I responded in less than 7 hours to a request that came in at 2 in the morning. What’s that saying? “A lack of planning on your part shouldn’t constitute an emergency on mine.” 🙂
Are figures with Golden Proportion really more attractive? explain pls help…….
The golden ratio has been used for centuries by many great artists, architects and designers to produce a natural harmony and beauty in their work, so it truly can be used to make any composition more attractive than one done without regard to the proportions within its design. See the page at https://www.goldennumber.net/category/design/ for a number of examples.
There are, however, a number of different elements and principles of design. The article at https://en.wikipedia.org/wiki/Visual_design_elements_and_principles shows them as:
Elements of design
1 Color
2 Line
3 Point
4 Shape
5 Texture
6 Space
7 Form
Principles of design
1 Unity/harmony
2 Balance
3 Hierarchy/Dominance/Emphasis
4 Scale/proportion
5 Similarity and contrast
Application of the golden ratio can impact unity/harmony, balance and scale/proportion and more, but it is just one aspect of good design. Good design thus requires more than just the application of the golden ratio, but the golden ratio can be used very effectively by those who understand its application to make design and composition better.
As cartoonist Stephen Silver says (https://www.goldennumber.net/golden-ratio-cartoon-character-design/), “The golden ratio is flawless because it gives the “small, medium and large” that design is built upon.”
Many thanks! My daughter will find this very helpful.
https://www.intmath.com/numbers/math-of-beauty.php
Me too doing maths project
i am doing a maths project too!!!
i am doing maths too!!!
Hey! Me too… 🙂
Im doing maths too lmao
Now I see the reasoning behind the ants in the movie Pi
wow, thats a genius 🙂 I love the Golden Ratio because its just so interesting! isn;t it amazing how EVERYTHING has a golden ratio? aweeesoooommeee
wish I could apply this golden ratio to picking the golden lottery numbers
I AGREE BUDDY
I wish to use this number in my program execution to control the sleep time of threads
NICE ARTICLE
I would submit the Phi symbol is perfect as a symbol of 0 intersected by 1 graphically and perfectly represents not division but the subquantum immanence or (un)presence of a metaphysical Unity, the Biblical I AM, where nothing, but everything, (un)resides …. what the physicist might refer to as the wave function with particle potential ..
Everywhere but nowhere … neither both nor neither
best translation? —> 🙂
I’ve had very similar thoughts, as expressed on the Theology page.
wave function is simply a tool to estimate a particle location not a universal property, same as super position and Schrodinger’s cat, the cat can not physically be dead and alive, we simply don’t have enough information for out tool, classic example of someone overthinking things, the observer does not affect the observed. tree falling in the woods anybody?
Do I understand this comment? I don’t think I do, please explain.
I thank this website was great and so was the picture of Mona Lisa
March 8, 2013 Corel Painter X … as you likely know has ‘Divine Proportion’ available as a guide for rendering file compositions. I first learned about ‘Golden Section’ from one of my art teachers, Mr. Flury at Art Center College of Design in Pasadena, CA. He had been on the staff at Disney Studios back with Walt, and was the archetype model inspiration for their cartoon animation character, Jiminy Cricket.
phenomenal
wow! for some reason i was late for church. p/u the kid section of the comics and saw the golden ratio. Just like the ratio, divine insperation led me here.
Thx!
Just as the square and the equilateral triangles give us two special right triangles, the pentagram gives us two more special right triangles resulting from two unique isosceles triangles found within the pentagram itself.
Great work.
I’d like newsletter or alerts to new findings of .618 or 1.618 in the world.
If phi is in most of life, it must be important.
I can help in research for u if u ever need it for a publication.
I am a money manager and I use phi in my work.
I think Phi is simply irrational.
Yes it is. It is an irrational number of a unique nature.. with its recurring decimals both in truth and in nature.
Interesting article. I wonder why it is not better taught in school. Then again, it is irregular, keeps on cropping up in life and seems to balance at this point.
Please help me with this.
so 1+square root of 5 divided by 2 equals 1.61803339….
But 1000 divided by 618 equals 1.6181229….
which is not the same and even more important
618 divided by 382 equals 1.617801…
which is not even 1.618 … I understand the principle but is A is the big line then A/B is not equal to B/C … it’s 1.618 and 1.617 …
1.618 and 0.618 are just rounded values used for simplicity when discussing the golden ratio. If you want more accuracy you must use more decimal places, e.g. 1.6180339887, or its actual value, e.g., the (square root of 5 + 1) / 2.
Very interesting, thank you! Do you know if and how Sacred Geometry can be used in hands-on healing?
Nice! Thanks for the information!
http://www.academia.edu/7736958/The_Sacred_Sanctuary_of_Makkah
For GODLY Design of Makkah (The Mother of all cities) as the ABSOLUTE REFERENCE POINT on earth please see the link above.
Best Regards,
Author
Salam Mr Fayar Tahir,
This is Astonishing! Thankyou
Regards,
Reader
Walaikum Salam Mr. Shafie.
Thanks for your comments.
Fayaz Tahir
I m working on my architectures design so that the building luks in d golden proportion frm each elevation… Thanx loads fuh d deap info!!
i love the article great work keep me updated regards
20 years ago I completed my Strathclyde University Degree dissertation based on the Golden ratio. In it, I had to prove that it did exist. In doing so, I subjected many of my friends, family and colleagues to questions relating to the Golden ratio. I used a simple piece of paper with a black dot marked at various places on the sheet. The sheets were A4 (UK) in size which, as you will know, use the Golden ratio for their paper size (A3 is double A4, etc, etc). The results were interesting. The engineers that I questioned predominantly felt that the ‘dot was most pleasing to the eye’ when shown at the exact centre of the page. The artists varied. Most other people (who generally did not think too deeply about art, measurements, science, etc) found that the ‘most pleasing place on the page where the dot was placed’ located it at the Golden ratio point. There were approx 150 people who were subjected to my questionning. The research was subsequently used by Nestle to identify where to align their corporate names on food/sweet wrappers for maximum effect. Unfortunately, I have never been able to get hold of my work and did not keep a copy. I will track down a copy one day when I visit Scotland. Thanks for reading.
The paper sizes are silver ratio not golden. They are called root 2 rectangles.
still cant apply the golden ratio to picking the lottery numbers HUMMM this may take years
There’s no reason to believe that the golden ratio can be used to pick lottery numbers, or any other method for that matter. Lottery numbers are selected by a process that produces RANDOM results, and that means they cannot be predicted.
You can use it to pick lottery numbers. It just won’t work.
Dr. Peter Mandel’s Esogetic Medicine utillizes Kepler’s information and many others to treat patients with color therapy. This therapy is similar to acupuncture and it utilizes colors. It is transmitted through the skin and doesn’t puncture it.
He utillizes alignment with the center of the pupil for many treatments. Throughout the body, there is proportionality in every treatment.
This is just one possible synchronicity in healing modalities.
An awesome article. This can be used for your success in life
It is also common for traders. I personally use Fibonacci for my trades and it help me to get successful trades.
Its useful for my architectures projects, Thanks Golden Number
φantastic
this is very interesting, i love it
I love the enthusiasm, Henry, I also love this almost as much as The golden ratui of my…
Gary, great to find a phi guy online. Writing to invite you to view the fine-tuned phi finds in ancient monument geodetic geometry, including Qin’s tomb and major American monuments, Newark, Pachacamac, Chavin, Tiwanaku, Tula, Chichen, and Machu Picchu (ArchaeoBlog link above). Perhaps you’ll have some insight to further understandings of what this conveys across time.
I have a page on the Great Pyramid at Giza on this at https://www.goldennumber.net/phi-pi-great-pyramid-egypt/, but do not have anything else on dimensions related to the golden ratio. There seems to be a clear connection between all these structures, some of which seem to be in alignment across the globe. If you come across any golden ratios in their proportions or positions I’d love to hear about it. You may find my software at http://www.phimatrix.com to be helpful in the analysis.
Already online as I wrote. See posts on: http://www.jqjacobs.net/blog/
Even a KML file: http://www.jqjacobs.net/kml/phi_golden_ratios.kml
I recently published a paper for Nexus Network Journal confirming the design of Khufu’s pyramid was indeed in golden ratio proportions (arguing Markowsky’s contention it was a misconception) supported by the fact that it was in the same proportions as the figure in ancient Egyptian art. ( Vol 16, No 2, 2014).
I have also discovered a meta-golden ratio rectangle (I use ‘chi’ for its symbol).
we know that if one removes a square from the end of golden ratio rectangle one is left with another phi rectangle. Whereas, the unique feature of a meta-golden chi rectangle is that if one removes a golden ratio rectangle from one end the remaining rectangle is another chi rectangle.
(Dirk Huylebrouck presented the math at Bridges Seoul 2014)
I
I have been experimenting with the Fibonacci number in my paintings and in checking out proportions of classical works. It’s a great means to structure abstractions. Curiosity got ticked in observing an old Bauhaus poster consisting of a triangle, a square and a circle: the combinations and relations never end. It’s fun and a great occupation during retirement; I am still painting…
Golden numbers are amazing. I found in 11×11 Pascal’s Triangle there are 11 sub-triangles that connect to each other and whose the sum of their numbers is a prime number and also there are also 11 fibonacci numbers inside that 11×11 P’s triangle! I haven’t tried it to higher nxn pascal’s triangle but i bet there must be other interesting pattern that connects Prime numbers and fibonacci numbers.
I think many-particle collisions must produce phi ratios automatically. Rick Mabry calculated that the hardest straight-in shot to make in snooker is when the object ball is golden ratio (61.8%) between cue ball and pocket.. assuming cue ball hit with normal distribution accuracy.. so if an “atom center” was surrounded by “shields” of particles, then the shields would be spaced at golden ratios to produce maximum deflection and protect the safe spot in the center.. atoms with less ideal shields would be destroyed faster.. so the center would become a low pressure and attract the shields.. could this cause the strong force.. and actually all forces like gravity? could a many-particle collision simulation be done to show how phi naturally forms? It must occur naturally coz it’s here.. just like proof by induction backwards.. if u go backwards in time you would unravel how golden ratio formed from many “shapes” of clusters of particles.. and at each moment everything just follows the master law: higher pressure moves to lower pressure, or 2 > 1
Great proof that I’m on the right track with what I’m painting …
“And if you should count the favors of God , you could not enumerate them”
This is the verse 16:18 of the chapter of Bee (#16 verse #18
It is somewhat related to counting the bounties of God- they never end, exactly like the golden ratio it keeps going. The word “God” corresponds to the letter #33 in the verse which is in the golden ratio: 1.18033
let’s take the application of Phi in beauty, thinking about this ratio being a constant number would mean beautiful things or faces would have the same consistency in design so as to achieve this constant, ultimately it would mean designing a perfectly beautiful subject would ultimately have a definite shape, which could never be altered in anyway, say for example, we want to design a human face from clay that actually embodies Phi, this would mean the nose would take a certain shape, so would other parts and sections of the face ultimately the face would have a definite shape which could never be changed in way if we dont want to temper with the constant. however, this is not the case in many of the actual faces we regard as beautiful in the sense that they are not actually the same, to some extent i could even say from just a thought that some of the beautiful face do not maintain the constant.
No project just an odd dream. I was trying to put together a golden key inside a tablet but I had to follow the fibonacci sequence. I didn’t know it. So I woke up trying to learn more about this golden ratio. Thank you so much you’re website is really informative and very well written!
Well I know understand how to work out golden ratio “the basics is enought for now and I now know how fibonacci sequence works! Thanks a dozen Mr. Meisner!!
design project on thesis
1.618=
One Dot (3,3) (6,6,6) =
The Way To God =
Circumpunkt=
Where you want to be
(It’s just coincidence, or is it “C Coins Dance”)
Does golden ratio have any impact on the subject of geometry?
Yes. See my entire section devoted to geometry at https://www.goldennumber.net/category/geometry/. Johannes Kepler, who discovered the true nature of orbits of bodies in space as ellipses, said this: “Geometry has two great treasures; one is the Theorem of Pythagoras; the other, the division of a line into extreme and mean ratio. The first we may compare to a measure of gold; the second we may name a precious jewel.” The “division of a line into extreme and mean ratio” is the description of the golden ratio that came from the writings of Euclid in ancient Greece.
I have preferred .618 for Phi. Many articles use 1.618. Why that form? Why not the more elementary .618
The articles use 1.618 because that is Phi, both by definition and by mathematics. The only positive solution to the formula that is used to calculate Phi is 1.618. See https://www.goldennumber.net/math/ for details.
Ohhh cool! The phi guy…author of this this that that. U’r a hardcore researcher. Like you. <3
thank you so much to the author for making this site…
it really helped me in my project and i didn’t had to go on other sites as everything that i wanted was given here so precisely. all the content was as per my expectations and factually correct.
once again thanks alot….
Thank you, Pratham, for your note of appreciation. I’ve tried for years to make this the best site on the web on this topic and sincerely appreciate your note.
Hi, I find the whole subject fascinating but have one simple question – what makes this ratio so attractive, so appealing in so many forms. Yes it may explain why a face appears beautiful or why a building appears marvelous in terms of proportion, but what is happening in our brain to make this ratio so appealing and satisfactory.
No one I have seen has ever explained this.
There is a study which explains the nature appeal of rectangles that have golden ratio proportions in width to height. It has to do with the function of our eyes:
https://www.theguardian.com/artanddesign/2009/dec/28/golden-ratio-us-academic
This, however, does not explain why the golden ratio appears more attractive as a dividing point, say in the distance of the lips between the eyes and chin. There is something more at work here, which is likely hard-wired into our perceptions of beauty.
I got it as close as i could get it with 3ds max… Still don’t know if I’m not seeing something right lol.
https://i.imgur.com/JTT2sav.png
The higher Golden Ratio Bar is a bit shorter then the one associated with the square in the middle.
I used the corners of the higher bar rather then the middle of each rectangle.
Its still not perfect.
The render angle and depth of the higher bar allows it to make it look more correct.
It took a long time. But I wanted to see if I could do it.
This is an accurate rendering of the two Phis… Triangle inscribed in a circle drawing.
https://postimg.org/image/5kvom5red/
this golden ratio was stolen from.india. and greeks have patented it. we indians were the first to invent zero all these were stolen from okerala.www.capt ajit vadayakil blog on secerts of Egyptian pypyramid
Well you did not find this number in the Bible but you can find it in the Quran’s chapter 3 Ayat 96 about Mecca.
Does your software or research explore phi in terms of sound and acoustics, in poetic speech, or dance choreography?
I have information on phi in sound, acoustics, and other topics that may be of interest at:
https://www.goldennumber.net/music/
https://www.goldennumber.net/acoustics/
https://www.goldennumber.net/poetry/
https://www.goldennumber.net/amen-break-golden-ratio-music/
My PhiMatrix software is a general purpose tool that aids in identifying and applying golden ratios. It does not specifically address any of the topics you listed, but could certainly be used whenever you have a digital representation/image of a topic and want to identify or create golden ratio points.
Hey!!I’m searching up for math assignment too!! Didn’t know it was so common a topic for projects.Nice work btw:)
I love Phi and Pi my parents are annoyed with me saying 3.14159265358979323846 and yes I memorized that. (I am only nine)
Congrats on your achievements. Very good for a nine year old. You’re kind of stuck with Pi, but you can express Phi with much more accuracy and perhaps less irritation to your parents by simply saying “(Root 5 plus 1) divided by 2!
Does golden ratio affects medical field?
Yes. The Golden Ratio is used in cosmetic facial and dental surgery to improve the appearance of the results. See:
https://www.goldennumber.net/beauty/
https://www.goldennumber.net/human-teeth/
goldennumber.net/health/
Hey, do you have any examples of how the Golden Ratio is applied to financial trading and the stock market?
Yes. See these pages for applications of the golden ratio and Fibonacci series to the financial markets:
https://www.goldennumber.net/fibonacci-stock-market-analysis/
https://www.goldennumber.net/forex/
https://www.phimatrix.com/stock-market-analysis/
I also received this as a math project, but the thing is, i dont get it, even when people are explaining it to me ;u;
The numbers in the golden spiral, what’s the point of them? And im sorry if you reply and i still dont understand ;-;
If this overview article doesn’t help, perhaps try the simpler yet explanation at https://www.goldennumber.net/what-is-phi/. The math involves a little algebra, but the concept is pretty simple. The golden ratio is simply the point at which you divide a line so that the ratio of the entire line to the large segment is EQUAL to the ratio of the large segment to the small segment. By contrast, if you divide a line at its midpoint, the ratio of the entire line to the half is 2 to 1 and the ratio of the two lines is 1 to 1. The golden ratio point occurs when that ratio is 1.618… for both proportions.
The numbers you’re seeing in the spiral are likely the numbers 1, 1, 2, 3, 5, 8, etc. That sequence is called the Fibonacci sequence, and the ratio of each number to the one before it gets closer to the golden ratio, 1.618…, as you go higher in the sequence. Those numbers can be arranged in a spiraling pattern to create a spiral that looks like the golden spiral. See more at https://www.goldennumber.net/spirals/.
And if that still all seems too mathematical, just know that the golden ratio is a unique number in mathematics, a bit like pi. It appears in nature and has been used in the arts to create works with a more natural harmony in their appearance.