Tiling in 5-fold symmetry was thought impossible!
Areas can be filled completely and symmetrically with tiles of 3, 4 and 6 sides, but it was long believed that it was impossible to fill an area with 5-fold symmetry, as shown below:
|
|
|
|
|
| 3 sides | 4 sides | 5 sides leaves gaps | 6 sides |
The solution was found in Phi, the Golden Ratio
In the early 1970’s, however, Roger Penrose discovered that a surface can be completely tiled in an asymmetrical, non-repeating manner in five-fold symmetry with just two shapes based on phi, now known as “Penrose tiles.”
This is accomplished by creating a set of two symmetrical tiles, each of which is the combination of the two triangles found in the geometry of the pentagon.
Phi plays a pivotal role in these constructions. The relationship of the sides of the pentagon, and also the tiles, is Phi, 1 and 1/Phi.
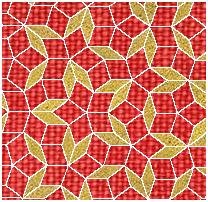
| The triangle shapes found within a pentagon are combined in pairs. | One creates a set of tiles, called “kites” and “darts” like this: | The other creates a set of diamond tiles like this: |
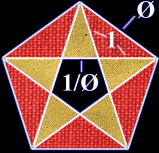 | 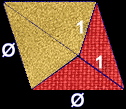 | 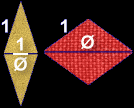 |
The ratio of the two types of tiles in the resulting patterns is always phi!
|
|
|
As you expand the tiling to cover greater areas, the ratio of the quantity of the one type of tile to the other always approaches phi, or 1.6180339…, the Golden Ratio.
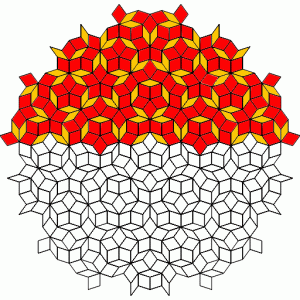
Within this tiling there can be small areas of five-fold symmetry. Decagons can also occur, which when grouped together can look like pentagons from a distance.
Explore further with these resources:
You can download a free program called “Bob” to generate Penrose tiling like the above at the site of Stephen Collins.
You can buy acrylic puzzles of Penrose darts, kites and tiles and other pentagon-based shapes at Kadon Enterprises.
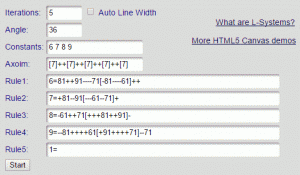
Create Penrose tiling with an L-System fractal generator. (See more on L-System) The input variables shown on the left create the pattern on the right. Note that the 36 degree angle is based on 360 degrees divided by 5 and then by 2, which relates it to the five-sided symmetry of Penrose tiling.
Quasi-Crystals
 |
Phi also gives 5-fold symmetry in 3D with a single shape, known as a quasi-crystal. |
Phi is intrinsically related to the number 5
The appearance of the golden ratio in examples of five-fold symmetry occurs because phi itself is intrinsically related to the number 5, mathematically and trigonometrically.
-
A 360 degree circle divided into five equal sections produces a 72 degree angle, and the cosine of 72 degrees is 0.3090169944, which is exactly one half of phi, the reciprocal of Phi, or 0.6180339887.
-
Phi itself is computed using the square root of five, as follows:
5 ^ .5 * .5 + .5 = Phi
In this mathematical construction, “5 ^ .5” means “5 raised to the 1/2 power,” which is the square root of 5, which is then multiplied by .5 and to which .5 is then added. See more on the Five and Phi page.






Hello! I’m doing an exploration on this topic for my IB Maths SL Exploration, is there anyway I could speak to you and ask a few things? I understand if that is too much to ask, thank you for this article anyway! It was really helpful.
This is so cool im doing my math SL IA on this topic as well. This artical is really helpful.
y’all chillin out in 2014 n 2015 doing math IAs on the golden ratio while I’m also doing the same thing but in 2018… this is wild, man.
This is cool, I’m also doing my math AI sl IA on golden ratio, wow
lol same
The Geometry Junkyard: Penrose Tiling
http://www.ics.uci.edu/~eppstein/junkyard/penrose.html
Ancient Islamic Penrose Tiles. Peter Lu uncovers evidence that the architects of a 500-year-old Iranian shrine used Penrose tiling to lay out the decorative …
Penrose Tiles Talk Across Miles
http://www.ams.org/samplings/feature-column/fcarc-penrose
It is obvious to me since told once as lad that pi was jot perfect that this all a manifestation of man not much else, measures from place to place, hence nothingb if divided enough is perfect aka water molecules must be measured by man for bond lengths and angles that we areive at man tryi:g to use math to:define these tiling concepts, in my opinion, i am looking:for:very simplenshapes:once on wikipedia to:whihc make:seemingly rectangular like tiles:for:ceilig all help:any help appreciatted williamrussellmorley at verizon net
Think in the black instead of the white and you will see the simplicity of Penrose tiling. It’s like the difference between painting (addition) and sculpting (subtraction) looking at a negative in opposite hues. …