Quasi-crystals and the Golden Ratio

Quasi-crystals represent a newly discovered state of matter.

Most crystals in nature, such as those in sugar, salt or diamonds, are symmetrical and all have the same orientation throughout the entire crystal.  Quasicrystals represent a new state of matter that was not expected to be found, with some properties of crystals and others of non-crystalline matter, such as glass.

With five-fold symmetry, once thought to be impossible, they were first observed in 1982 in an aluminiun-manganese alloy (Al₆Mn).  Since then, quasicrystals have been found in other substances.

Quasi-crystals fill space with five-fold symmetry based on phi.

Penrose tiles allow a two-dimensional area to be filled in five-fold symmetry, using two shapes based on phi.  It was thought that filling a three-dimensional space in five-fold symmetry was impossible, but the answer was again found in phi.

Where the solution in 2D required two shapes, this can be accomplished in 3D with just one shape.  The shape has six sides, each one a diamond whose diagonals are in the ratio of phi:

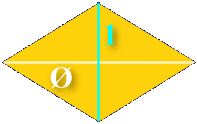
The resulting solid looks like this:

Download and print this to make your own!

A Nobel Prize for Quasi-Crystal Discovery was awarded in 2011.

As reported in “2011 Nobel Prize in Chemistry: ‘Quasicrystals’ once thought impossible have changed understanding of solid matter” by ScienceDaily on October 14, 2011 athttp://www.sciencedaily.com/releases/2011/10/111005080232.htm:

The Royal Swedish Academy of Sciences has decided to award the Nobel Prize in Chemistry for 2011 to Daniel Shechtman of the Technion — Israel Institute of Technology in Haifa, Israel, for the discovery of quasicrystals: non-repeating regular patterns of atoms that were once thought to be impossible.

In quasicrystals, we find the fascinating mosaics of the Arabic world reproduced at the level of atoms: regular patterns that never repeat themselves. However, the configuration found in quasicrystals was considered impossible, and Daniel Shechtman had to fight a fierce battle against established science. The Nobel Prize in Chemistry 2011 recognizes a breakthrough that has fundamentally altered how chemists conceive of solid matter.

On the morning of April 8, 1982, an image counter to the laws of nature appeared in Daniel Shechtman’s electron microscope. In all solid matter, atoms were believed to be packed inside crystals in symmetrical patterns that were repeated periodically over and over again. For scientists, this repetition was required in order to obtain a crystal.

Shechtman’s image, however, showed that the atoms in his crystal were packed in a pattern that could not be repeated. Such a pattern was considered just as impossible as creating a football using only six-cornered polygons, when a sphere needs both five- and six-cornered polygons. His discovery was extremely controversial. In the course of defending his findings, he was asked to leave his research group. However, his battle eventually forced scientists to reconsider their conception of the very nature of matter.
Aperiodic mosaics, such as those found in the medieval Islamic mosaics of the Alhambra Palace in Spain and the Darb-i Imam Shrine in Iran, have helped scientists understand what quasicrystals look like at the atomic level. In those mosaics, as in quasicrystals, the patterns are regular — they follow mathematical rules — but they never repeat themselves.

When scientists describe Shechtman’s quasicrystals, they use a concept that comes from mathematics and art: the golden ratio. This number had already caught the interest of mathematicians in Ancient Greece, as it often appeared in geometry. In quasicrystals, for instance, the ratio of various distances between atoms is related to the golden mean.

Following Shechtman’s discovery, scientists have produced other kinds of quasicrystals in the lab and discovered naturally occurring quasicrystals in mineral samples from a Russian river. A Swedish company has also found quasicrystals in a certain form of steel, where the crystals reinforce the material like armor. Scientists are currently experimenting with using quasicrystals in different products such as frying pans and diesel engines.

History of the findings

These findings came about as follows:

• In the mid-1970s the mathematician Roger Penrose created an aperiodic mosaic, with a pattern that never repeats itself, using only two different tiles: one fat rhomboid and one thin rhomboid. He called these kites and darts and named this finding Penrose tiles.
• In 1982, Dan Shechtman captured a picture with an electronic microscope that seemed counter to all logic. The ten bright dots in each circle revealed that he was seeing tenfold symmetry. Conventional wisdom said that this was against the laws of nature.
• In 1982, Alan Mackay experimented with a model in which circles representing atoms were placed at intersections in Penrose’s mosaic. He illuminated the model and found a tenfold diffraction pattern.
• In 1984, Paul Steinhardt and Dov Levine connected Mackay’s model with Shechtman’s actual diffraction pattern. They realized that aperiodic mosaics helped to explain Shechtman’s unusual crystals.

Implications for other geometries

One of the most amazing implications of this property is that it’s not just 5-fold symmetry that is made possible. The unexpected find is that with quasiperiodicity, a whole new class of solids is possible! Any symmetry in any number of dimensions becomes attainable! Here are some examples of other symmetries from a presentation by P.J. Steinhardt titled “What are quasicrystals?”

References:

https://www.nobelprize.org/nobel_prizes/chemistry/laureates/2011/popular-chemistryprize2011.pdf

http://www.i-sis.org.uk/Golden_Mean_Wins_Chemistry_Nobe_Prize.php

http://www.physics.princeton.edu/~steinh/QuasiIntro.ppt