Leonardo Fibonacci discovered the sequence which converges on phi.
In the 1202 AD, Leonardo Fibonacci wrote in his book “Liber Abaci” of a simple numerical sequence that is the foundation for an incredible mathematical relationship behind phi. This sequence was known as early as the 6th century AD by Indian mathematicians, but it was Fibonacci who introduced it to the west after his travels throughout the Mediterranean world and North Africa. He is also known as Leonardo Bonacci, as his name is derived in Italian from words meaning “son of (the) Bonacci”.
Starting with 0 and 1, each new number in the sequence is simply the sum of the two before it.
0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377 . . .
This sequence is shown in the right margin of a page in Liber Abaci, where a copy of the book is held by the Biblioteca Nazionale di Firenze. Click to enlarge.
The relationship of the Fibonacci sequence to the golden ratio is this: The ratio of each successive pair of numbers in the sequence approximates Phi (1.618. . .) , as 5 divided by 3 is 1.666…, and 8 divided by 5 is 1.60. This relationship wasn’t discovered though until about 1600, when Johannes Kepler and others began to write of it.
The table below shows how the ratios of the successive numbers in the Fibonacci sequence quickly converge on Phi. After the 40th number in the sequence, the ratio is accurate to 15 decimal places.
1.618033988749895 . . .
Compute any number in the Fibonacci Sequence easily!
Here are two ways you can use phi to compute the nth number in the Fibonacci sequence (fn).
If you consider 0 in the Fibonacci sequence to correspond to n = 0, use this formula:
fn = Phi n / 5½
Perhaps a better way is to consider 0 in the Fibonacci sequence to correspond to the 1st Fibonacci number where n = 1 for 0. Then you can use this formula, discovered and contributed by Jordan Malachi Dant in April 2005:
fn = Phi n / (Phi + 2)
Both approaches represent limits which always round to the correct Fibonacci number and approach the actual Fibonacci number as n increases.
The ratio of successive Fibonacci numbers converges on phi
| Sequence in the sequence | Resulting Fibonacci number (the sum of the two numbers before it) | Ratio of each number to the one before it (this estimates phi) | Difference from Phi |
| 0 | 0 | ||
| 1 | 1 | ||
| 2 | 1 | 1.000000000000000 | +0.618033988749895 |
| 3 | 2 | 2.000000000000000 | -0.381966011250105 |
| 4 | 3 | 1.500000000000000 | +0.118033988749895 |
| 5 | 5 | 1.666666666666667 | -0.048632677916772 |
| 6 | 8 | 1.600000000000000 | +0.018033988749895 |
| 7 | 13 | 1.625000000000000 | -0.006966011250105 |
| 8 | 21 | 1.615384615384615 | +0.002649373365279 |
| 9 | 34 | 1.619047619047619 | -0.001013630297724 |
| 10 | 55 | 1.617647058823529 | +0.000386929926365 |
| 11 | 89 | 1.618181818181818 | -0.000147829431923 |
| 12 | 144 | 1.617977528089888 | +0.000056460660007 |
| 13 | 233 | 1.618055555555556 | -0.000021566805661 |
| 14 | 377 | 1.618025751072961 | +0.000008237676933 |
| 15 | 610 | 1.618037135278515 | -0.000003146528620 |
| 16 | 987 | 1.618032786885246 | +0.000001201864649 |
| 17 | 1,597 | 1.618034447821682 | -0.000000459071787 |
| 18 | 2,584 | 1.618033813400125 | +0.000000175349770 |
| 19 | 4,181 | 1.618034055727554 | -0.000000066977659 |
| 20 | 6,765 | 1.618033963166707 | +0.000000025583188 |
| 21 | 10,946 | 1.618033998521803 | -0.000000009771909 |
| 22 | 17,711 | 1.618033985017358 | +0.000000003732537 |
| 23 | 28,657 | 1.618033990175597 | -0.000000001425702 |
| 24 | 46,368 | 1.618033988205325 | +0.000000000544570 |
| 25 | 75,025 | 1.618033988957902 | -0.000000000208007 |
| 26 | 121,393 | 1.618033988670443 | +0.000000000079452 |
| 27 | 196,418 | 1.618033988780243 | -0.000000000030348 |
| 28 | 317,811 | 1.618033988738303 | +0.000000000011592 |
| 29 | 514,229 | 1.618033988754323 | -0.000000000004428 |
| 30 | 832,040 | 1.618033988748204 | +0.000000000001691 |
| 31 | 1,346,269 | 1.618033988750541 | -0.000000000000646 |
| 32 | 2,178,309 | 1.618033988749648 | +0.000000000000247 |
| 33 | 3,524,578 | 1.618033988749989 | -0.000000000000094 |
| 34 | 5,702,887 | 1.618033988749859 | +0.000000000000036 |
| 35 | 9,227,465 | 1.618033988749909 | -0.000000000000014 |
| 36 | 14,930,352 | 1.618033988749890 | +0.000000000000005 |
| 37 | 24,157,817 | 1.618033988749897 | -0.000000000000002 |
| 38 | 39,088,169 | 1.618033988749894 | +0.000000000000001 |
| 39 | 63,245,986 | 1.618033988749895 | -0.000000000000000 |
| 40 | 102,334,155 | 1.618033988749895 | +0.000000000000000 |
Tawfik Mohammed notes that 13, considered by some to be an unlucky number, is found at position number 7, the lucky number!
The Fibonacci Sequence and Gambling or Lotteries
Some people hope that Fibonacci numbers will provide an edge in picking lottery numbers or bets in gambling. The truth is that the outcomes of games of chance are determined by random outcomes and have no special connection to Fibonacci numbers.
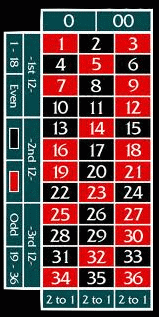There are, however, betting systems used to manage the way bets are placed, and the Fibonacci system based on the Fibonacci sequence is a variation on the Martingale progression. In this system, often used for casino and online roulette, the pattern of bets placed follows a Fibonacci progression: i.e., each wager should be the sum of the previous two wagers until a win is made. If a number wins, the bet goes back two numbers in the sequence because their sum was equal to the previous bet.
In the Fibonacci system the bets stay lower then a Martingale Progression, which doubles up every time. The downside is that in the Fibonacci roulette system the bet does not cover all of the losses in a bad streak.
An important caution: Betting systems do not alter the fundamental odds of a game, which are always in favor of the casino or the lottery. They may just be useful in making the playing of bets more methodical, as illustrated in the example below:
| Round | Scenario 1 | Scenario 2 | Scenario 3 |
| Bet 1 | Bet 1 and lose | Bet 1 and lose | Bet 1 and win |
| Bet 2 | Bet 1 and lose | Bet 1 and lose | Bet 1 and win |
| Bet 3 | Bet 2 and win | Bet 2 and lose | Bet 1 and lose |
| Bet 4 | – | Bet 3 and win | Bet 1 and lose |
| Bet 5 | – | – | Bet 2 and win |
| Net Result | Even at 0 | Down by 1 | Ahead by 2 |
DANTS FORMULA IS THE LOG OF ONE DEFINED DIMENSION TO THE DIVISION OF ITSELF
I am very curious about the “sequence” and how it affects us as people in our daily lives. John says it is the combinations of moves and or optimization one must make in order to complete a task, taking in scenarios in which one would never lose. Could you point me to more information how this connects with our lives, past, present and future? and if in laymen terms that would be much better.
i like the no. 46368 as much as 317811.
FIBONACCI is the combinations of moves and or optimization
one must make inorder to complete a task, taking in scenarios
in which one would never lose.
How would i describe the relationships you discovered in the Fibonacci sequence?
Thank you for your input and clarification sir. The original way is golden! You can never loose! Any other way can lead to a path of darkness and confusion as you try to come full circle.
I love the column, but it hits something of a pet peeve. Check out
http://en.wikipedia.org/wiki/Series_(mathematics)
to see the distinction between a sequence and a series. Basically, everywhere you see the word “series”, it should be “sequence”. Instead of “Sequence in the series”, how about “Position in the sequence”.
Thank you for the insight on this. There seem to be differing definitions depending on the source. Dictionary.com defines series as “a group or a number of related or similar things, events, etc., arranged or occurring in temporal, spatial, or other order or succession; sequence” followed by “Series, sequence, succession are terms for an orderly following of things one after another. Series is applied to a number of things of the same kind, usually related to each other, arranged or happening in order: a series of baseball games. Sequence stresses the continuity in time, thought, cause and effect, etc.: The scenes came in a definite sequence. Succession implies that one thing is followed by another or others in turn, usually though not necessarily with a relation or connection between them: succession to a throne; a succession of calamities.” Google lists 1.2 million references for “Fibonacci Series” and 2.1 million references for “Fibonacci sequence” so both are in common usage, although sequence is apparentely more prevalent. I’ll review your suggested changes and include these comments to the post for clarification.
Gary – Very interesting article and table. FYI, Patrick is correct that series and sequence have specific meanings and are not interchangeable to mathematicians, no matter what Google or various dictionaries say. To mathematicians, a sequence is a progression of numbers generated by a function, whereas a series is the sum of numbers in a sequence. Your article is too good in other respects to use these terms in non-mathematical ways.
Best,
Lou
Thanks, Lou. I’ve taken your advice and changed the references in the article to sequence from series.
And a product as well.
I am very curious about the “sequence” and how it affects us as people in our daily lives. John says it is the combinations of moves and or optimization one must make in order to complete a task, taking in scenarios in which one would never lose. Could you point me to more information how this connects with our lives, past, present and future? and if in laymen terms that would be even better.
Thanks for your kind consideration of my request.
Cheers Shelley
i am to0.
He must have been absolutely amazing figuring this out without calculators.
is the difference from phi column actually an inverted fibonacci series where you skip one number each time? 1+2=3, 2+3=5 but only 1,2 & 5 are in the sequence. next is 14, 36…
Thank you …
How brilliant he must have been. And now we use calculators. Thanks — Martin
I think the real brilliance comes from the Indian mathematician Acharya Pingala
“In Europe, Fibonacci’s Liber Abaci in 1202 describe these numbers; the book was meant to introduce the Indian number system and its mathematics which he had learnt in North Africa from Arab teachers while a young man growing up there. Fibonacci speaks of his education in North Africa thus: “My father, who had been appointed by his country as public notary in the customs at Bugia acting for the Pisan merchants going there, summoned me to him while I was still a child, and having an eye to usefulness and future convenience, desired me to stay there and receive instruction in the school of accounting. There, when I had been introduced to the art of the Indians’ nine symbols through remarkable teaching, knowledge of the art very soon pleased me above all else and I came to understand it.”
Nor sure if you’ve seen the work done by artist Vi Hart posted on Kahn Academy. If not, enjoy. Love your site.
https://www.khanacademy.org/math/recreational-math/vi-hart
Here we are in 2020 and I found your comment on this site! What a fantastic video, thank you for sharing all those years ago! Fascinating how Mathematics is always relevant and “hidden” in the world around us.
It was really awesome. Now I really think that most of us die without knowing fractions of things around us, It was one among of those.. Thanks for sharing.
awesome!!!!!!!!!!!!!!!!!!!!!!!!!!
Hey Gary Meisner,
Excellent article for the Fibonacci series of course this blog is doing a very good job of serving useful information. I’m proud to be a part of its Readers community.
For the Fibonacci programs in different languange like C language,JAVA,C# must visit http://www.hhhprogram.com/2013/05/fibonaccci-series.html
Thank you hardik for your Good job.
Is it posible that Fibonaccis Sequence could explane the bigbang or how time started????
Yes, the big bang was the result of the Golden Number being divided by zero. So, never do that!
Eros.
Good humor. Division by zero is known to mess up calculators and spreadsheets, but current thinking in cosmology reflects a different cause. There is an interesting relationship though between 0 divided by 1 and Phi discussed on Theology page.
That doesn’t sound like chance, (big bang). That sounds like perfect order.
https://groups.google.com/d/msg/sci.physics.relativity/EHtG-Zz33_Q/zcSOIzVAQA8J
http://physics.nist.gov/cgi-bin/cuu/Value?mu0%7Csearch_for=universal_in!
4pi x 2 x 3 x 5
0.99930819635258
Value 376.730 313 461… Omega
Standard uncertainty (exact)
Relative standard uncertainty (exact)
Concise form 376.730 313 461… Omega
(376.7303146)/(4*π*2*3*5)*300000000
299792458.90577
Spirit science talks alot of this subject. I believe its called sacred geometry. It shows alot of the ways phi and fibonaci occur EVERYWHERE in the universe. From conch shells to DNA, to expanding galaxies! The whole series is very informative, a new perspective of seeing the things we see constantly.
“EVERYWHERE” is not completely accurate. It appears many places, but many spirals in nature are just equiangular spirals and not golden spirals.
I was looking for the real time application of Fibonacci Sequence and got it from your blog. Thank you Very Much for your awesome Article.
One can begin with any two random numbers and as long as the Fibonacci pattern is followed, they will eventually come out to 1.6180339–!
That is true. The Fibonacci numbers have some very unique properties of their own, however, and there’s something mathematically elegant to start with 0 and 1 rather than two randomly selected numbers. Either way, this illustrates the significance of the additive property of the Fibonacci series that allows us to derive phi from the ratios of the successive numbers.
However, Fibonacci sequence converges faster than other similar sequences.
CAN ANYONE TELL ME WHAT IS THE RATIO OF AN ANGLE OF GOLDEN TRIANGLE???????
Adarsh, a “ratio” requires two things. Your question isn’t clear because you don’t say what two things you want the “ratio” of.
I noticed that there is actually an “exact” Fibonacci sequence. If you use phi (0.618…) as the first number and one as the second number, you get the sequence:
0.6180339887, 1, 1.6180339887, 2.6180339887, 4.2360679775, 6.8541019662…
I say it is “exact” because the ratio between successive terms is always exactly Phi (1.618…), with no approximation. This sequence has some interesting properties. The terms actually begin to approach integers as they get larger.
The sequence of exponential powers of phi does have unique properties, but technically speaking it is not the sequence discovered by Fibonacci and named after him.
Hi Gary,
If the Fibonacci sequence is the sequence starting with 1, what do we call the infinite number of other sequences whose ratios all converge on Phi in a similar manner?
Any two starting numbers, including fractions or even negative numbers, in any combination, will work.
Regards,
Ted.
Sorry, misspelled Fibonacci!
Ted.
That depends on who invent the series. yes, there are many such series out there, but we need to identify them and need to prove their concept in front of the world. Publishing a paper on it will do the task.
Great Article, thank you very much for shedding some much deserved light on this forgotten gem!!
I use the sequence for my Keno picks. I have only just begun learning what the numbers together meant when I did a google search for the repeating ratios I was seeing day after day when Fibonacci caught my attention…since a little self-education in Math I won a single Keno game yesterday for $625 using the Fibo-technique!!! Now I won’t let anyone tell me that the numbers are random. They only appear to be random because the Fibonacci sequence has been hidden away from the masses.
I’m happy to hear that you won a single Keno game, but that hardly establishes that you’ve found a method. I can assure you that it was just random good luck and had absolutely nothing to do with using numbers in the Fibonacci sequence.
Lotteries, Keno and everything other such game of chance are completely random in their outcomes. I had one person who assured me once that he had discovered a Fibonacci pattern in the California Lottery. I downloaded about 10 years worth of winning numbers and plotted them on a graph for him. It looked like the static “pattern” you see on your TV when there is no signal. There was no pattern at all.
Play if you want for entertainment, but don’t bet anything you can’t afford to lose and don’t ever think the house/casino is dumb enough to stack the odds in anyone’s favor but their own. Good LUCK to you!
that’s pretty easy
thanks for helping :))))))))))))))))))))))
To mathematicians, a sequence is a progression of numbers generated by a function, whereas a series is the sum of numbers in a sequence. Your article is too good in other respects to use these terms in non-mathematical ways.
Indeed. But a sequence need NOT be “generated by a function.” E.g.,
2 6 13 8 1 41 (power ball choices, say), is a sequence. I may or may not wish to sum the sequence or form its product. Naf Saratoga CA 😉
OK: again . USUALLY generated. The prime numbers form a sequence; One can surely determine them using various techniques, but no one can generate them.
Unless you, perhaps, have solved RH. Or something related thereto.
Naf
Exception:
“Random Sequence. A sequence that is irregular, non repetitive, and hapahazard. … …
A completely satisfactory definition of randomn sequence is yet to be discovered. However, test of randomness can be made; e.g., by subdividing the sequence into blocks and using the chi-square test to to analyze the frequencies of occurrence of specified individual integers… … …A table of one million random digits has been published”
I’ve also noticed that the ratio of successive pairs of numbers in other sum sequences converge as well. For example, take any three numbers and sum them to make a fourth, then continue summing the last three numbers in the sequence to make the next. The ratio of successive pairs of numbers in this sequence converges on 1.83928675521416….
Similarly, summing the last four, five, six, seven and eight numbers converge on different values which themselves appear to converge on 2.0 as you increase the quantity of numbers which are summed. ie.;-
Numbers Convergent value
Summed
2 1.61803398874989…
3 1.83928675521416…
4 1.92756197548293…
5 1.96594823664549…
6 1.98358284342433…
7 1.99196419660503…
8 1.99603117973541…
Regards,
Ted.
I guess I should have Googled this earlier;-
http://en.wikipedia.org/wiki/Generalizations_of_Fibonacci_numbers
Regards,
Ted.
I do appreciate and you have done nice work!! and i always use http://en.wikipedia.org/wiki/Series_(mathematics), gives more information
can someone tell me who the author of this article is? I would love to credit him or her for this wonderful job in my math project.
Unless otherwise noted, all articles on this site are written by Gary Meisner. See https://www.goldennumber.net/content-images-use for details on references.
Mr. Hawthorne’s comment is interesting, especially with respect to dictionary definitions.
One sees that not all sequences can be generated by a function.
The random sequence is one such (pg 247, Mathematics Dictionary, James & James, 5th Ed 1992.)
“Random Sequence. A sequence that is irregular, non repetitive, and hapahazard. … …
A completely satisfactory definition of random sequence is yet to be discovered. However, test of randomness can be made; e.g., by subdividing the sequence into blocks and using the chi-square test to to analyze the frequencies of occurrence of specified individual integers… … …A table of one million random digits has been published”
Njs
Mr. Hawthorne’s comment is interesting, especially with respect to dictionary definitions.
One sees that not all sequences can be generated by a function.
The random sequence is one such (pg 247, Mathematics Dictionary, James & James, 5th Ed 1992.
“Random Sequence. A sequence that is irregular, non repetitive, and hapahazard. … …
A completely satisfactory definition of randomn sequence is yet to be discovered. However, test of randomness can be made; e.g., by subdividing the sequence into blocks and using the chi-square test to to analyze the frequencies of occurrence of specified individual integers… … …A table of one million random digits has been published”
Njs
How brilliant he must have been. And now we use calculators. Thanks for this informative article.
solved 432hz divided by 2 216,108,54, 27,13.5,6.75,3.375,1.6875 the atom inside a nucleus my head ,the one inside ,can see alot.
Now a days we use calculators….How brilliant he must have been.
can u pls tell me dat which Indian or in which Indian book phi is discovered 1st
Archarya Pingala wrote a treatise on this etc —-Chandaḥśāstra
Everything is still SO Western-euro centric but it is good to see the world waking up to different perspectives and acknowledgements
In Europe, Fibonacci’s Liber Abaci in 1202 describe these numbers; the book was meant to introduce the Indian number system and its mathematics which he had learnt in North Africa from Arab teachers while a young man growing up there. Fibonacci speaks of his education in North Africa thus: “My father, who had been appointed by his country as public notary in the customs at Bugia acting for the Pisan merchants going there, summoned me to him while I was still a child, and having an eye to usefulness and future convenience, desired me to stay there and receive instruction in the school of accounting. There, when I had been introduced to the art of the Indians’ nine symbols through remarkable teaching, knowledge of the art very soon pleased me above all else and I came to understand it.
Correct pronunciation is FEE
Like many other words in the English language, the answer depends on who you ask and where you ask it. See https://www.goldennumber.net/pronouncing-phi/ for a more in depth discussion.
Question:
If you pick a random number N (lets say 17) and N+1 (18) and started the sequence from those two numbers, does the series converge on phi or some other infinite series?
You can start with any two numbers, add then together and continue in the same way and the ratio of the larger to the smaller will converge on phi.
The sequence of exponential powers of phi does have unique properties, but technically speaking it is not the sequence discovered by Fibonacci and named after him
There is even more to this brilliance of the (phi) magic as the synchronous nature of the letters PHI serve us as a mnemonic acronym for the languages (Polish-Haitian-Igbo) as the New World Order of the Northwest manifest a spoken “Golden Motto” phrase from the well of the almighty Torus; a surface of revolution generated by revolving a circle in three-dimensional space throat. In military quantum theology theory this is equivalent to the word of God and or All other collective deities of the X, Y, and Z axis. RAK II
A Fibo fact I want to share:
ONE+ONE+TWO+THREE+FIVE+EIGHT = 13×21
The sum of gematrias of the 6 first Fibos gives the product of the 2 next terms with an incredible reciprocity:
1x1x2x3x5x8 = THIRTEEN+TWENTYONE
The product of the 6 first Fibos gives the sum of gematrias of the 2 next terms
See the verification here http://www.gef.free.fr/gem.php?texte=ONE+ONE+TWO+THREE+FIVE+EIGHTTHIRTEEN+TWENTYONE
That’s a rather amazing intersection of numbers and letters. For those who aren’t familiar with “gematria” it simply means in this case assigning a number value to each letter. A = 1, B = 2, C = 3, D = 4, etc. This works for the Fibonacci numbers in English. What about other languages?
Thanks for this equation.
Fibonacci sequence converges faster than other similar sequences. Plus, you can start it with any two numbers.
I’m no mathematician or scientist, but from what I understand about bra-ket notation, just about everything grows and then decays according to logarithmic spirals and whirling squares, represented by PSI and PHI.
And what I’ve read seems to say that there are other possible logarithmic spirals the universe could be based
on, but the PHI spiral is the slowest of all, and using any of the others would have made it impossible for life on earth to exist at all! Any expert opinions out there to shed more light on this notion?
Heard of Hypatia?
Yup… great female thinker and scientist of her time in Egypt. Sadly condemned by those ‘pious’, ‘self-righteous’ and intolerant ignoramii Christians of her time. First for being an outspoken woman and second for defying normal conventions and her intelligence.
To Peter Hedding
Please tell me more about bra-ket notion! It’s very important to me. I want to use in a lottery game. If it possible for you I think it’s gonna be okay to describe more than one lottery strategies. Perhaps you help me to win this lottery:
http://australian-lotto-results.com/ozlotto
Thanks!
However, this mathematical sequence has been already descrived in Vedas and long later By Aryabhatta and Bhaskar- the great scholars of Vedic culture of Nepal. http://www.tushitanepal.com
I first became interested in the Fibonacci sequence when I asked one of my high school science teachers how he explained that curls of hair and desert sand dunes seen from above seem to have the same pattern. He mentioned Fibonacci and Pascal and I was hooked. But the picture that stands out most as a Fibonacci reminder is that of a green vegetable resembling a broccoli.
Fibonacci number patterns do appear in nature, but be careful in using them as an explanation. Most curves and spirals in nature, particularly in non-living examples, are simply equiangular / logarhymic curves, which expand at an equal pace throughout the curve and have nothing to do with Fibonacci numbers or the golden ratio.
It’s called a Romanesco broccoli..
The so-called Fibonacci set was actually discovered by the ancient Indian mathematician Pingala in the 2nd or 3rd century BCE (the same guy who discovered binary system).
Can someone tell me WHY fibonacci thiught it was interesting
I wonder if one could use this function to predict human history based on past prectable behaviors to certain social/historical/psychological stimuli- kinda like psychohistory in Asimov’s Foundation series.
Check Mandelbrot is fun… Don’t think to much about sequences or you will end finding that pi was also revered in Ancient Greece,
Been studying for years and I couldn’t really find a real life application of phi yet. But good explanation though.
You may want to extend your study to a few more pages on this site. Lots of real life applications here:
https://www.goldennumber.net/category/design/
https://www.goldennumber.net/category/face-beauty/
https://www.goldennumber.net/category/life/
https://www.goldennumber.net/category/markets/
Try my theistic challenge: Team up with God and take a weekend getaway to Las Vegas. The food and entertainment are excellent and inexpensive. Gamble just $100. Stop when you have either lost the $100—never gamble more than you can afford to lose—or until you walk away with $800. Donate the profit to your church or a religious cause. Note that betting the entire $100 on red or black on the roulette table requires only three wins to accumulate $800. Only three wins! (The probability of this happening is almost 1 out of 9. ) Even if you lose the $100, you will enjoy the experiment. But are the odds actually against you?
Suppose you decided to wager only $100 on red in roulette. If you lose you quit. If you win, you let the $200 ride. If you lose, you go home. If you win again ($400), you let it ride one last time. You either pick up $800, or go home having lost only your initial $100. In fact, of the eight equally likely possibilities you win $800 once and lose $100 seven times. That is an expected WIN of $100 for you. Proof: Just count the eight equally likely possibilities where even one loss (L) sends you home without your $100: WWW, WWL, WLW, LWW, WLL LWL, LLW, LLL. Let’s go to Las Vegas!
One of my favorite movies Run Lola Run (1998, German with subtitles, R-rated) has the poor, desperate-but-virtuous main character asking God for help to save her boyfriend’s life. She looks up from the street and sees a casino. Quite a scene follows.
anyone know how Fibonacci. figured all of this out with only his mind in the 17th century. and might i ask why do we need the Fibonacci sequence?