The Fibonacci Series is found in Pascal’s Triangle.
Pascal’s Triangle, developed by the French Mathematician Blaise Pascal, is formed by starting with an apex of 1. Every number below in the triangle is the sum of the two numbers diagonally above it to the left and the right, with positions outside the triangle counting as zero.
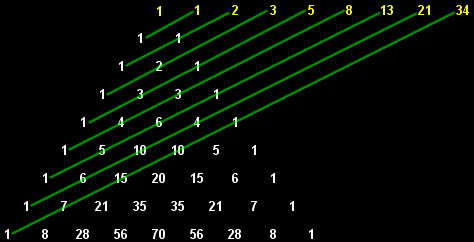
The numbers on diagonals of the triangle add to the Fibonacci series, as shown below.
Pascal’s triangle has many unusual properties and a variety of uses:
-
Horizontal rows add to powers of 2 (i.e., 1, 2, 4, 8, 16, etc.)
-
The horizontal rows represent powers of 11 (1, 11, 121, 1331, 14641) for the first 5 rows, in which the numbers have only a single digit.
-
Adding any two successive numbers in the diagonal 1-3-6-10-15-21-28… results in a perfect square (1, 4, 9, 16, etc.)
-
It can be used to find combinations in probability problems (if, for instance, you pick any two of five items, the number of possible combinations is 10, found by looking in the second place of the fifth row. Do not count the 1’s.)
-
When the first number to the right of the 1 in any row is a prime number, all numbers in that row are divisible by that prime number



thnx
what is this? i want it’s construction.
The illustration above shows how the numbers on the diagonals of Pascal’s triangle add to the numbers of the Fibonacci series. What other type of construction do you seek? Perhaps you can find what you seek at Pascal’s Triangle at Wikipedia.
Wonderful video. I love approaching art and degisn from a maths and scientific angle and this illustrates that way of working perfectly. Plus, I only just noticed the link to further explanations so it’s even more exciting.Great post.
the exterior of the triangle is made up of 1’s and the rest of the numbers are each the sum of their neighbours from the row above them. 2=1+1, 4=3+1, 21=6+15, etc.
Ohhhhh. Now I get it! Thank you soo much!
This is used for algebra
no its not
:/
Uh, yes it is Harvey. One common use is for binomial expansion.
Yes, it is. As Heather points out, in binomial expansion.
For instance (X+Y)^4 = 1 XXXX + 4 XXXY + 6 XXYY + 4XYYY + 1YYYY
where the coefficients ( 1, 4, 6, 4, 1 ) are the fourth row of Pascal’s Triangle.
Hey that is very helpful and all but what is the formula to work out the triangle?
Every number in the triangle is the sum of the two numbers diagonally above it to the left and the right, with positions outside the triangle counting as zero.
Thanks
This is good source of information. I used to get ideas from here. Is pascal’s triangle found in fibonacci sequence?
yes it does on the shallow diagonals
(a+b)^7 solve
a^7+a^6*b+a^5*b^2+a^4*b^3+a^3*b^4+a^2*b^5+a*b^6+b^7
Almost correct, Joe. Remember to include the coefficients.
That’s where Pascal’s triangle comes in… so (a+b)^7 = 1*a^7 + 7*a^6*b + 21*a^5*b^2 + 35*a^4*b^3 + 35*a^3*b^4 + 21*a^2*b^5 + 7*a*b^6 + 1*b^7.
hello, so good information about maths
Thanks this helped SOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOO MUCH.
Hi,
Can you explain how Pascal’s triangle works for getting the 9th & 10th power of 11 and beyond?
Thanks,
Vikrant
if you see each horizontal row as one number (1,11,121,1331 etc.) it will show the powers of 11 just carry on the triangle and you should be able to find whatever power of 11 your looking for
Carry over the tens, hundreds etc so 1 5 10 10 5 1 becomes 161051 and 1 6 15 20 15 6 1 becomes 1771561.
1
…5
…1 0
…….1 0
…………5
…………….1
___________+
1 6 1 5 1
I agree with kyle v.i.h ftw.
Interesting
You can represent the triangle as a square. Rows & columns represent the decimal expension of powers of 1/9 (= o.111111 ; 1/81 = 0,0123456 ; 1/729 = 0.00136.)
This is such an awesome connection. I hadn’t seen that before. Thanks for the visual!
Hi, just wondering what the general expression for Tn would be for the fibonacci numbers in pascal’s triangle? Thanks
This is so useful thanks so so so so so much 😉
the 2nd statement is not at all true, The horizontal rows represent powers of 11 (1, 11, 121, 1331, 14641, 1621051!=.15101051, etc…)
only works for the first 5 rows
11^0=1
11^1=11
11^2=121
11^3=1331
11^4=14641
11^5=161051 is different than 15101051
Good observation. Correction made to the text above. Thanks.
It also works below the 5th line. You just carry the tens digit into the previous column
****11^5=161051 is different than 15101051***
1,5,10,10,5,1
1(5+1)(0+1)051
1(6)(1)051
Finding your presentation and explanation of Pascal’s Triangle was very interesting and its analysis amusing.
What is remarkable is to find how each number fits in perfect order inside the triangular matrix to produce all
those amazing mathematical relationships. Thank you so much..!!!
A bit of modification in the horizontal representation resulting in powers of 11 can turn it into a general formula for any power . It goes like this- Instead of choosing the numbers directly from the triangle we think each number as a part of a decimal expansion i.e. 1 2 1 =(1 x 100) +(2 x 10) + (1 x 1) . = 11^2 . Similarly it works even for powers greater than 5, for example : 1 6 15 20 15 6 1 = 11^6….. and so on 😉
do you think this is pascal’s ?
1
4 9
16 25 36
49 64 81 100
121 144 169 196 225
You can also find sierpinski’s triangle by marking all odd numbers
Althought known as Pascal’s triangle, apparently Pascal himself wrote it as a square. As a square rows and columns represent negative powers of 9 (10-1).
1 1 1 1 1 1
1 2 3 4 5
1 3 6 10
1 4 10
1 5
1
1/9 = 0,1111111
1/81=0,0123456
1/729= 0.00137
etc.
(using 1/99…. will avoid carrying over of decimals)
Addiing up those fractions ‘aproaches’ the ratio 1/8 = 0,125 (0,1249999999…..)
Similar the infinite sum of negative powers of 90 (1/90) results in 1/89, which decimally represents the diagonal sum of Pascal’s triangle:
1 1 1 1 1 …
0 0 1 2 3 4 …
0 0 0 0 1 3 6 …
0 0 0 0 0 0 1 4 …
0 0 0 0 0 0 0 0 1 …
—————————— +
1 1 2 3 5 …
Another application:
(1x) 21 =
(1x) 8 + (1x) 13 =
(1x) 3 + (2x) 5 + (1x) 8 =
(1x) 1 + (3x) 2 + (3x) 3 + (1x) 5 =
(1x) 0 + (4x) 1 + (6x) 1 + (4x) 2, (1x) 3 = 21
An inverse example:
(1x) 0 =
(1x) 1 + (1x) -1 =
(1x) -1 + (2x) 2 + (1x) -3 =
(1x) 2 + (3x) -3 + (3x) 5 + (1x) -8 =
(1x) -3 + (4x) 5 + (6x) -8 + (4x) 13 + (1x) -21 = 0
So I don’t understand. What does it mean when it says “the numbers on the diagonals add to the Fibonacci series”. Which diagonals is this referring to, and how does this add to make the sequence?
See the illustration. The green lines are the “diagonals” and the numbers of the Pascal’s triangle they intersect sum to form the numbers of the Fibonacci sequence – 1, 1, 2, 3, 5, 8, …
Looking at it this way might help:
1
0 1
1 0 1
0 2 0 1
1 0 3 0 1
0 3 0 4 0 1
1 0 6 0 5 0 1
Row sum = Fibonacci sequence
I was trying to find the fibonacci sequence in the pascal’s triangle. This website is so useful!!!
I am working on the following problem. I realized that the underlying structure IS the Fibonacci sequence. In order to solve the problem, I need a way to compute the diagonals shown above in a computationally efficient way.
I.e., I need a way to efficiently compute the following sequences:
– 1
– 1 1
– 1 2
– 1 3 1
– 1 4 3
– 1 5 6 1
– 1 6 10 4
– 1 7 15 10 1
– …
Ideally, to compute the nth sequence would require time proportional to n. One way that this could be achieved is by using the (n-1)th sequence to compute the nth sequence.
If there happens to be a way to compute the nth sequence in constant time, that would be fantastic.
Problem:
There is a fence with n posts, each post can be painted with one of the k colors.
You have to paint all the posts such that no more than two adjacent fence posts have the same color.
Return the total number of ways you can paint the fence.
Note:
n and k are non-negative integers.
Example:
Input: n = 3, k = 2
Output: 6
Explanation: Take c1 as color 1, c2 as color 2. All possible ways are:
post1 post2 post3
—– —– —– —–
1 c1 c1 c2
2 c1 c2 c1
3 c1 c2 c2
4 c2 c1 c1
5 c2 c1 c2
6 c2 c2 c1
It says when the first number right to 1 is prime, it divides all in the raw , but it should be all except first and last numbers in the raw.