Fibonacci numbers and Phi are related to spiral growth in nature.
If you sum the squares of any series of Fibonacci numbers, they will equal the last Fibonacci number used in the series times the next Fibonacci number. This property results in the Fibonacci spiral, based on the following progression and properties of the Fibonacci series:
12 + 12 + 22 + 32 + 52 = 5 x 8
12 + 12 + . . . + F(n)2 = F(n) x F(n+1)

A Golden spiral is very similar to the Fibonacci spiral but is based on a series of identically proportioned golden rectangles, each having a golden ratio of 1.618 of the length of the long side to that of the short side of the rectangle:

The Fibonacci spiral gets closer and closer to a Golden Spiral as it increases in size because of the ratio of each number in the Fibonacci series to the one before it converges on Phi, 1.618, as the series progresses (e.g., 1, 1, 2, 3, 5, 8 and 13 produce ratios of 1, 2, 1.5, 1.67, 1.6 and 1.625, respectively)
Fibonacci spirals and Golden spirals appear in nature, but not every spiral in nature is related to Fibonacci numbers or Phi. Most spirals in nature are equiangular spirals, and Fibonacci and Golden spirals are special cases of the broader class of Equiangular spirals. An Equiangular spiral itself is a special type of spiral with unique mathematical properties in which the size of the spiral increases but its shape remains the same with each successive rotation of its curve. The curve of an equiangular spiral has a constant angle between a line from origin to any point on the curve and the tangent at that point, hence its name. In nature, equiangular spirals occur simply because the forces that create the spiral are in equilibrium, and are often seen in non-living examples such as spiral arms of galaxies and the spirals of hurricanes. Fibonacci spirals, Golden spirals and golden ratio-based spirals often appear in living organisms.
Alternate spirals in plants occur in Fibonacci numbers.
The most common appearances of a Fibonacci numbers in nature are in plants, in the numbers of leaves, the arrangement of leaves around the stem and in the positioning of leaves, sections and seeds.
Here a sunflower seed illustrates this principal as the number of clockwise spirals is 55 (marked in red, with every tenth one in white) and the number of counterclockwise spirals is 89 (marked in green, with every tenth one in white.)

Pinecones and pineapples illustrate similar spirals of successive Fibonacci numbers, with the example below showing the alternating pattern of 8 and 13 spirals in a pine cone.

Click on an image below to see the full size versions of each image above:
Golden spirals in sea shells
Golden ratios are also sometimes found in the proportions of successive spirals of a sea shell, as shown below.
The Nautilus shell spiral is not a Golden spiral but often still has Golden Ratio proportions.
The nautilus shell is often shown as an illustration of the golden ratio in nature, but the spiral of a nautilus shell is NOT a golden spiral, as illustrated below. The golden spiral overlay is provided by PhiMatrix golden ratio software:
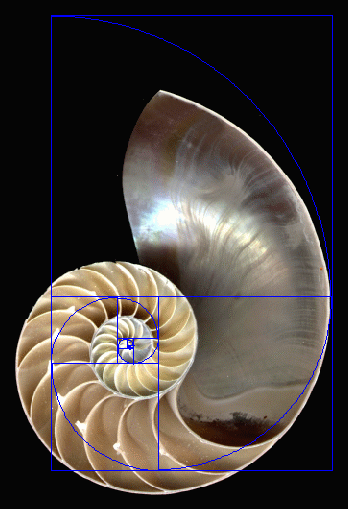
Nautilus shell spiral compared to a Golden Spiral
The Nautilus spiral, however, while not a Golden spiral, often displays proportions its dimensions that are close to a golden ratio, appearing in successive rotations of the shell as the Nautilus grows. As with all living organisms, there is variation in the dimensions of individuals, so the appearance of the golden ratio is not universal.

See also other examples and explanations of the golden ratio in the nautilus spiral.







having to do with the way energy nests itself into matter: note the mammalian ear cochlea; and how the lower tones which carry the farthest are sensed in the tightest spirals, and the higher tones, nearest, in the larger. Fascinating. Thank Fibonacci; otherwise, we’d have to be fascinated all over.
It’s fascinating how this pattern occurs through all of creation. We have just posted a video by Drunvalo Melchizedek that touched breifly on the fibonacci and the golden mean, which lead me to do some more research which lead me here. Thanks
merry christmas
Awesome site! Thanks for the help and inspiration.
Yes. Netscape….IM me on the MySpace!…seriously, does the golden ratio have anything to with our gravity specific to earth? I’ m thinking water spiraling through drain/toilet?? Btw, I’m not THAT educated, this could have already been covered?
Maybe I’ll ogle it…google it.
-“comedy Devine, idea mine.”
amazing!
So much great info, thanks.
Great pictures and explanations on PHI —thanks
helped a bit tar
it´s fascinating:-)
appreciate the images and moving demonstrations!
Very interesting, thank you, but I would like to be able to stop animation of the pine cone, so that I can examine it more closely. Just my preference!
I totally agree that the animated pine cones would have been enjoyable to look at and linger over as still images
The still images are there for your viewing pleasure too. Just click on any of the three images below the animated image and the stills will open in full size in a gallery.
It has to do with the slow growth rate of organisms and gravitational pull and rotation of the earth. Nature has to have a starting and stoping point. Our species is about at the end of our growth and technology rates… Prepare accordingly, we are all gonna die soon. Mothman Prophecy
https://www.youtube.com/watch?v=LkWp_KpcFNQ
Very good site!! Thanks for the moving demonstrations! Really helped for my maths assignment!
Thanks this cleared up my confusion between the Fibonacci series and the Golden Spiral.
I’m having problems drawing this in a CAD program…. the arc commands won’t replicate the spiral precisely. I am literally trying to draw it in the FibanaccI rectangle pattern and can’t make it work! Any ideas?
You’re likely experiencing two issues:
The spiral created by squares of progressive Fibonacci numbers is only an approximation of the spiral created by adjacent golden rectangles. You’ll be closer if you build the spiral using golden rectangles.
Even then, using a circular arc from the corners of the squares in a golden rectangle is only an approximation of a true golden ratio spiral. To get it perfect you would need to have graphing capabilities and the formula for the golden ratio spiral. See https://en.wikipedia.org/wiki/Golden_spiral for details.
These spirals appears in stable solitons on superfluids, check this Sculptures….
This work is amazing ?. I could watch these wind sculptures fir hours , wow.
The Density Wave Theory explains the Spiral movement of Galaxies:
Here’s an example of how some interesting features emerge from interference patterns produced by spirals:
Very nice article about spirals, golden ratio and Nature. Ser below a kind of contribution… https://jorgexerxes.wordpress.com/2017/12/12/golden-ratio-sequence/
I love this.
Innate my
Attraction.
Infinite
And formal.
Sexy as hell.
I have been to your website several times over the years. Phi facinates me. I am currently working on an article about Phi. I wanted to see if a painting i was doing of a Datura flower was a golden spiral. The spiral is like a nautalis spiral. Thank you for all of your work.
Thanks for the appreciation, Sydney. See also the article at https://www.goldennumber.net/nautilus-spiral-golden-ratio/ on differences between the golden spiral and the Nautilus spiral. Also note the my PhiMatrix design software at http://www.phimatrix.com has golden spiral overlays to measure and apply spirals.
In nature, equiangular spirals occur simply because they result in the forces that create the spiral are in equilibrium,
This sentence is grammatically incorrect.
You may wish to edit.
Spiral and Golden ratio is most helpful and our daily life as well us in mathematics. you see the golden ratio being used more than you think you do. Actually, you probably see it being used almost every day. Just as the golden ratio looks nice in paintings, it also looks nice when used in logos. like The Pepsi logo, Toyota logo, Hyundai logo, i Cloud logo, Apple logo and Twitter logo.
Those patterns is extremely pleasing to the eye. We now have scientific evidence that our brains automatically recognize this pattern. Whether we have been genetically programmed to like it or we find it pleasing due to all the examples around us, the golden ratio has been used for a long time.
Our learning experience about the Golden Ratio isn’t over yet, we intend to learn more about this topic and many others as we continue our journey to become the best student we can be! We are also excited to start learning new things each day in our classroom right along with our future teachers as we discover the magic of mathematics and other subjects together!
Well said, and you can see illustrations of its appearance in logos on my pages at https://www.goldennumber.net/logo-design/ and https://www.goldennumber.net/google-logo-design-golden-ratio/. And that’s just the beginning of its applications in the arts, as shown at https://www.goldennumber.net/category/design/. And the discoveries keep coming, with the latest from the quantum physics to black holes.
it was interesting to know that the spiral shape have numbers is it more challenge to computing numbers
I just want to say that I am so amazed with fibonacci numbers
Pretty racist that the series is not named Pingala series.
I agree that it’s unfortunate anytime that credit isn’t given where it is due, but I think we need to use caution before instantly playing the race card. Racism is defined as “a belief that race is a fundamental determinant of human traits and capacities and that racial differences produce an inherent superiority of a particular race.” I don’t see how that is at play here. There are other factors involved. First, there are language differences that make it difficult for one civilization to know and credit another’s discoveries. Second, many aspects of knowledge are independently “discovered” by many people of time simply by observation and application, without even knowing if someone has had the same discovery, or who or when that might have been. Third, in the past there was more focus on just sharing knowledge that was an accumulated from a variety of sources rather than claiming individual ownership through naming, copyrights, etc. Still, it would be good for those in non-Western civilizations to get credit for their work and contributions in Western history and literature.
your explanations and images to enhance them are as elegant as what you describe. thank you for such an informative and beautiful site.
This Ratio and Spiral was so satisfying:-)
It showed some pattern of number then it turned into different kind of boxes until it when spiral, because of the pattern and later on resulted with a beautiful kinds of things related to nature.
What I learned in this video is mathematics is not just a number, but All of the things in this world are inspired by numbers, measurements,and computation. In short all of the things that we see are example of mathematics. And also remind us that the mathematics have intimate relationship between nature.
Good day,
May I please use the pine cone images in a book I am publishing in Afrikaans (my mother tongue) in South Africa?
Hi Willem. I responded to your email with details. For general use of images see https://www.goldennumber.net/content-images-use/.