Phi appears in a number of geometric constructions using circles.
There are a number of geometric constructions using a circle which produce phi relationships, as described below.
Among mathematicians, there’s a bit of a competition to see how few lines can be used to create a phi proportion, or golden section, in the construction, or how many golden sections can be created with the least number of lines.
Three circle construction:
Put three circles with a diameter of 1 (AB and DE) side by side and construct a triangle that connects the bottoms of the outside circles (AC) and the top and bottom of the outside circles (BC). The dimensions are as follows:
AB = 1
AC = 2
BC = √5
DE = 1
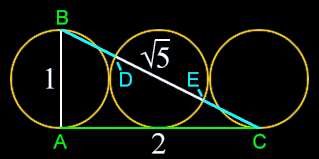
The line BC thus expresses the following embedded phi relationships:
BE = DC = (√5-1)/2+1 = (√5+1)/2 = 1.618 … = Phi
BD = EC = (√5-1)/2 = 0.618… = phi
This simple and elegant way of expressing the most standard mathematical expression of Phi was discovered and contributed by Bengt Erik Erlandsen on 1/11/2006.
Equilateral triangle construction:
Insert an equilateral triangle DEF inside a circle. Find the midpoints of each leg at ABC.
The ratio of the length of segment AG to segment AB is Phi, or 1.618 0339 887 …
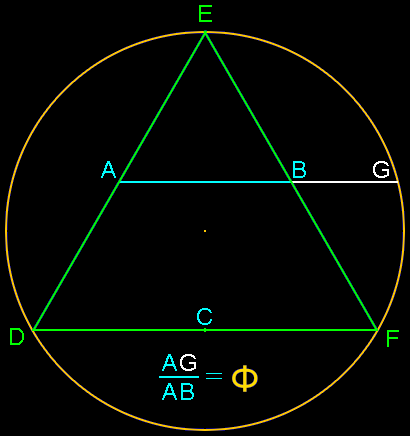
This construction was developed by George Odom and published in American Mathematics Monthly, 90 (1983) 482, with the solution in 93 (1986) 572.
Enhanced equilateral triangle construction:
Here’s a very interesting enhancement to the basic equilateral triangle construction above:
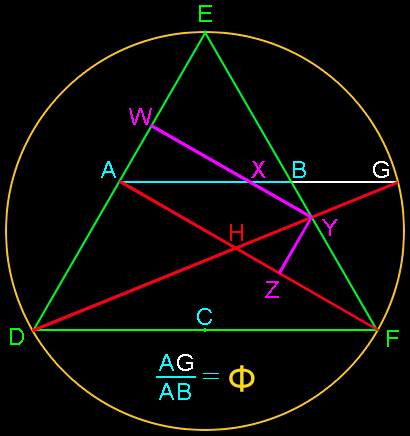
Connect the points with lines at AF and DG (in red).
At Y, the intersection of DG and EF, create perpendicular lines from Y to AF at Z, and again from Y to ED at W.
This produces a number of phi relationships, or golden sections:
| Line segment | Golden section point | Segments in phi relationship |
| AG | B | AG to AB |
| EF | Y | EF to EY |
| AF | Z | AF to AZ |
| EA | W | EA to EW |
| WY | X | WY to WX |
| Arc EGF | G | EF to EG |
Can you find more phi relationships? If so send them in!
This construction, while similar to the Odom construction, was developed independently by Hans J. Dettmer as an elegant solution to dividing a prism in equal volumes, as described in the attached paper.
Concentric circle construction:
Here’s a construction using three concentric circles whose radiuses are in a ratio of 1 : 2 : 4.
Draw a tangent from the small circle through the other two, crossing points A and B and extending to G.
The ratio of the length of segment AG to segment AB is Phi, or 1.618 0339 887 …
Proof: AB = 2 * 3½ and AG = 15½ + 3½, which by factoring out the 3½ can be reduced to a ratio of 2 to (5½+1), or Phi.
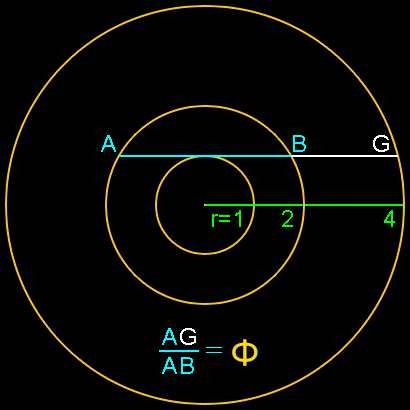
This construction was developed by Sam Kutler and submitted by Steve Lautizar.
Overlapping circles construction:
This construction can be created by simply drawing five circular arcs.
Construct concentric circles of radius 1 and 2 with a center point at C.
Construct concentric circles of radius 1 and 2 with a center point at D.
Draw a line from the intersection points of the two smaller circles at A
to the intersection point of the two larger circles at G.
The ratio of the length of segment AG to segment AB is Phi, or 1.618 0339 887 …
Proof: AB/AG = ( 2 Ö 3 ) / ( Ö15 + Ö3) = 2 / ( Ö5 = Ö1) = 2 / ( Ö5 = Ö1) = Phi
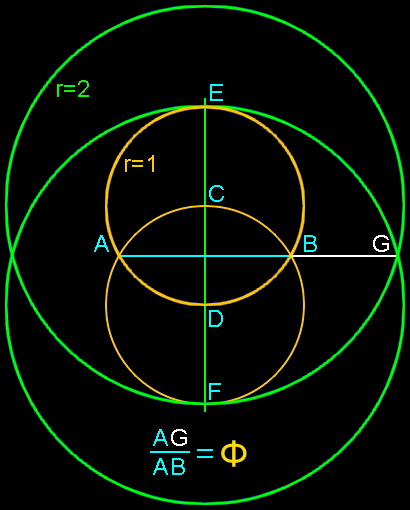
This construction was developed by Kurt Hofstetter in 2002 and published in Forum Geometricorum, Volume 2 (2002) 65-66.



Binary code is done as 0 and I…
0 = Nothing
I = Something
0 + I = Φ
Or, as stated on the Theology page, 1 or Unity can also represent God so that Creation, based on Phi, is created from God from Nothing.
Credo che il cerchio sia già la dimostrazione di ciò che hai detto.
Il cerchio, come parte misurabile, può esistere solo grazie ad un punto detto centro, non misurabile.
I believe the circle is already proof of what you said. The circle, as a measurable part, can exist only thanks to a point called the center, which is not measurable.
Thanks for the article Gary. It is nice to know how to find phi ratio in circles. I am learning as much as I can about phi, I am sure this article will light the way ahead. I do find myself wondering, how does the nature plot to create concentric circles. I mean she does not measure them up.
Probably, I need to read more. However, this article was a worthy stop-by.
That’s so wonderful !
I love it
Simply beautifull
Hi Gary,
Thanks for your insight. I think I find Phi even more interesting than Pi. However I would like to extrapolate what happens when you inscribe other geometric figures inside the circle. So far we have Pi = the ratio of the circumference of the circle to its diameter, Phi is the ratio of the circumference of the circle to the equilateral triangle etc. but what magic do we have with the circumference of the circle to the square, the pentagon, the hexagon …the nagon? With the number of sides this ratio of course approaches 1.
With respect to the phi “magic” of the square and pentagon, see the constructions at https://www.goldennumber.net/geometry/. Not every polygon though up to one with an infinite number of sides relates to phi.
Something seems (to me) to be missing from the “Overlapping circles construction”
What sets the spacing between points C and D?
My first construction attempt almost nailed Phi (a few PPM too large.)
Moving C and D even a small amount makes a big difference in the ratio AB/BG
C is the center of the circle with a radius of length CD, also CE.
With D now known, D is the center of the circle with the same radius length DC, also DF.
You can’t move C and D. They’re the center and circumference of the same circle.
How can the second one (Equilateral triangle construction) be proved?
See https://www.cut-the-knot.org/do_you_know/GoldenRatio.shtml.
Non so se sia pertinente al meraviglioso tema trattato, volevo condividere una considerazione nata dalla contemplazione del cerchio e dalla sua definizione geometrica. ” L’insieme dei punti equidistanti da un punto detto centro ”
L’insieme dei punti appartengono al Regno del misurabile, quindi materiale.
Ma questo insieme non può esistere senza la sua origine , cioè quel Punto detto centro , non misurabile, quindi non materiale.
Mi sembra quasi una dimostrazione matematica che la materia (il mondo conosciuto) possa esistere solo grazie alla non materia o spirito. Forse non nell’uno ma nello zero la vera natura divina.
I do not know if it is pertinent to the wonderful subject dealt with, I wanted to share a consideration born from the contemplation of the circle and its geometric definition. “The set of points equidistant from a point called the center”. The set of points belong to the realm of the measurable, therefore material. But this set cannot exist without its origin, that is, that Point called the center, which is not measurable and therefore not material. It seems to me almost a mathematical demonstration that matter (the known world) can exist only thanks to non-matter or spirit. Perhaps not in the one but in the zero the true divine nature.
holy (blank)!