Using the Golden Ratio to win at football.
 The golden ratio is found in many places, but here’s one you might not have expected: It can be found in football gaming strategy when making the “point after touchdown” decision as to whether to kick for 1 extra point or go for a 2 point conversion.
The golden ratio is found in many places, but here’s one you might not have expected: It can be found in football gaming strategy when making the “point after touchdown” decision as to whether to kick for 1 extra point or go for a 2 point conversion.
This applies to the situation when a team is trailing by 14 points late in a football game, and then scores a touchdown to be trailing the other team by 8 points.
So what should you do: Kick for 1 point after touchdown (PAT) or go for a 2 point conversion?
Most football teams kick the PAT in this situation, but in fact it is (almost) always better to go for 2. The reason is related to phi.
If your odds of making a 2 point conversion are at least 38.2% (1/phi^2), you should then should go for 2.
This finding and the analysis presented below was contributed by Alexander (Alex) Leach. He is a high school football coach and physics teacher in Texas, and was using statistics to help make the decision as to whether to kick for 1 extra point or go for a 2 point conversion. In doing so he found this exact application of the golden ratio to gaming strategy for football.
Typical logic might tell you that you need a 50% chance of converting to justify going for 2 but this is inaccurate. The reason is that you can adjust your strategy after you know the outcome of your 2 point try.
Here are the relevant situations:
- Kick the PAT for 1 point (-7), score again (-1), Kick again (tied), play in OT, versus
- Convert for 2 points, with:
- Convert (-6), score again (tied), kick a PAT (+1 and win), or
- Fail to convert (-8), score again (-2), attempt a 2 point (-2 or tied) to play in OT
Assuming that kicking the PAT is 100% and the odds of winning in OT are 50%. Then it works out that the odds needed to justify going for 2 are exactly 1/Phi^2, or 38.2%
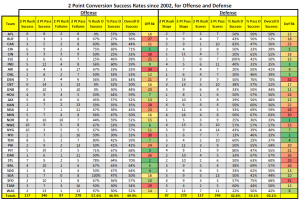
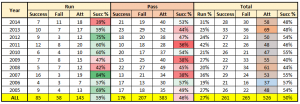
Professional football two point conversion success rates
Interesting enough, professional football teams have a much better chance of make the two point conversion than 38.2%, so this analysis is very relevant to a team’s probability of winning a game. Look at the following statistics by team and by year, and note that the overall success rate of making the two point conversion is almost 50%!
Source: www.SharpFootballAnalysis.com
Alex’s more in depth explanation below explains the exact relationship to phi, the math, the logic, and all possible outcomes.
Golden ratio in statistics of football strategy
There is an exact application of phi when looking at statistics used when deciding to go for a 2 point conversion after a touchdown. The specific situation it applies to is when deciding what to do after scoring when down 14 points. Most charts say to go for 1, but in fact it is usually better to go for 2 in that situation. If you consider the odds of kicking your Point After Touchdown (PAT) to be 100%, it is still better to go for 2 as long as you have about a 38.2% chance of converting on your 2-point play. Actually the payoff of the two strategies breaks even when your odds of converting are exactly 38.2%. There are several ways to express 38.2% using Phi (1.618), including:
- ((1/phi)²)
- (2-phi), or
- (1-1/phi)
Here is the logic and implied math:
Suppose your team is down 14 points with time running out and you score a touchdown to make it down 8 point behind. You can kick a PAT or attempt a 2-point conversion. There are only a few relevant situations that should weigh into the decision.
Here are those relevant situations and likelihood of each.
- Odds of converting a 2 point = C
- Odds of kicking a PAT = K
- Odds of winning in OT =T
- Odds of scoring again without other team scoring = A
When you choose to kick it, the odds of winning = KAKT+ (1-K)ACT
- (kick)(good)(score again)(kick)(good)(win OT): W = KAKT
- (kick)(good)(score again)(kick)(good)(loose OT): L = KAK(1-T)
- (kick)(good)(score again)(kick)(no good): L = KA(1-K)
- (kick)(no good)(score again)(go for 2)(good)(win OT): W = (1-K)ACT
- (kick)(no good)(score again)(go for 2)(good)(loose OT): L = (1-K)AC(1-T)
- (kick)(no good)(score again)(go for 2)(no good): L = (1-K)A(1-C)
When you choose to go for 2, the odds of winning = CAK+ CA(1-K)T+ (1-C)ACT
- (go for 2)(good)(score again)(kick)(good): W = CAK
- (go for 2)(good)(score again)(kick)(no good)(win OT): W = CA(1-K)T
- (go for 2)(good)(score again)(kick)(no good)(loose OT): L = CA(1-K)(1-T)
- (go for 2)(no good)(score again)(go for 2)(no good): L = (1-C)A(1-C)
- (go for 2)(no good)(score again)(go for 2)(good)(win OT): W = (1-C)ACT
- (go for 2)(no good)(score again)(go for 2)(good)(loose OT): L = (1-C)AC(1-T)
We can find the point where the payoff for the two strategies are equal by setting the formulas equal to each other. So:
- Odds kicking= KAKT+ (1-K)ACT = CAK+ CA(1-K)T+ (1-C)ACT = Odds going for 2
Dividing by A gives us (odds of scoring again should have no factor on decision because both strategies require another score):
- KKT + (1-K)CT = CK + C(1-K)T + (1-C)CT
Assuming you have a 50/50 chance of winning in OT, so T=.5, we get:
- .5(KK+(1-K)C) = CK + .5C(1-K) + .5C(1-C)
Now for simplifying: (skip to the bottom unless you want to see the math, and forgive me if I have a typo)
Solving for K first:
- Expanding: KK/2-CK/2+C/2=CY/2+C/2+C(1-C)/2
- Move to left: KK/2-CK-C(1-C)/2=0
- For Quadratic equation form: KK-2KC-C(1-C)=0
So we can complete the square:
- KK-2KC=C(1-C)
- Adding CC to both sides: KK-2KC+CC=C(1-C)+CC
- Simplify the right: KK-2KC+CC=C
- Writing left side as square: (K-C)(K-C)=C
- Square rooting both sides: K-C=sqrt(C) Or K-C = -sqrt(C)
- Solve for K: K=C +or- sqrt(C)
Similarly we can solve for C:
- Starting from our original : .5(KK+(1-K)C) = CK + .5C(1-K) + .5C(1-C)
- In standard form: C(1-K)/2+KK/2=-CC/2+C(.5+{1-K}/2+K)
- Move to left: CC/2+C(1-K)/2-C(.5+{1-K}/2+K)+ KK/2=0
- In standard form: CC/2+ C((1-K)/2-.5+{K-1}/2-K)+ KK/2=0
- Quadratic equation: CC + 2C((1-K)/2-.5+{K-1}/2-K)+KK=0
So we can complete the square:
- CC + 2C((1-K)/2-.5+{K-1}/2-K)=-KK
Completing the square:
- CC+2C((1-K)/2-.5+{K-1}/2-K)+((1-K)/2-.5+{K-1}/2-K)^2=-KK+ ((1-K)/2-.5+{K-1}/2-K)^2
- Factor the left: (C+(1-K)/2-.5+{K-1}/2-K)^2=.25(4K+1)
- Square root: (C+(1-K)/2-.5+{K-1}/2-K)= +or- .5(4K+1)
- Solve for C: C=.5+(1-K)/2+(K-1)/2+K +or- .5(4K+1)
So by solving we get: (assuming K and C are real, positive, and from 0 to 1)(they are)
- K=C+sqrt(C), or
- C=(2K – sqrt(4K+1) +1)/2
Now if we assume K=1 and solve for C we get:
- (K=1 when odds of kicking a PAT are 100%, true odds in NFL are 99.3%*)
- C=.381966011250105
This is the point where the odds of winning are the same using either strategy. This is also one of the 2 percentages most closely related to phi.
When you divide your odds of not converting by your odds converting it equals phi exactly.
- (1-C)/C=phi
There are several other ways to relate this number to phi. Here are a few examples:
- C=1-(1/phi)
- C=2-phi
- C=3-Phi^2
- C=1/phi^2
Verification of the results
For those of you who would like to test this out without going through all the steps, you can let the formula solver at WolframAlpha.com do the hard work for you.
Start with Alex’s equation above: KKT + (1-K)CT = CK + C(1-K)T + (1-C)CT
With K=1 and T=0.5, simplify it as: 1*1*.5 + (1-1)C*5 = C*1 + C(1-1)*.5 + (1-C)C*.5
Go to the formula solver at https://www.wolframalpha.com/examples/EquationSolving.html
Enter this as the polynomial equation: solve 1*1*.5 + (1-1)C*5 = C*1 + C(1-1)*.5 + (1-C)C*.5, or just click on this solution link.
The results will show as :
C = 1/2 (3-√(5))
C = 1/2 (3+√(5))
The first one is 0.382, which is 1 / Phi ².
The Golden Rule of Football
So that’s the golden rule for football. Do unto others as you would have them do unto you is great wisdom and the golden rule for life. In football, the golden rule is to use mathematics and the golden ratio as a strategy in making your game decisions. It can make the difference between winning and losing.



Fascinating, the Golden Ratio and Football (Soccer to our American friends), also have a deeper relationship, via computational complexity Universality and the Asynsis Constructal paradigm.
https://www.quantamagazine.org/20141015-at-the-far-ends-of-a-new-universal-law/
https://medium.com/@ASYNSIS/no-dick-tators-yes-curators-cd782f9f5e36#.4iazx07sh
http://www.scoop.it/t/asynsis-principle-constructal-law
Hi there!
I’m doing a school project offer the random occurrences of phi, and I just so happened to stumble upon this. I’m truly fascinated! I’ve been going through all of the math, and it actually works (not that I thought it was wrong, it’s just insane that it actually works!) However, I am confused as to why you add CC to both sides when trying to solve for K. Could you please provide why this step was needed? I hope this post is still monitored!
The explanation of the math may have to come from Alexander (Alex) Leach, the contributor of the article, or one of the other mathematicians reading this site. If I can find time to circle back to this I will, but typically adding a variable to both sides is just done to allow a grouping to take place that allows for further simplification of the equation. Any takers?
It was simply a method to isolate K from any other variables.
Hi, i wan’t to ask a question.
“When you divide your odds of not converting by
your odds converting it equals phi exactly.”
What does “converting” in this sentence mean?
Converting means to score the point after the touch down, either 1 point from a kick, or 2 points by running/passing the ball into the end zone.
Thank you so much.