Phi is most often calculated using by taking the square root of 5 plus 1 and divided the sum by 2:
√5 + 1
2
This mathematical expression can be expressed geometrically as shown below:
Three circle construction:
Put three circles with a diameter of 1 (AB and DE) side by side and construct a triangle that connects the bottoms of the outside circles (AC) and the top and bottom of the outside circles (BC). The dimensions are as follows:
AB = 1
AC = 2
BC = √5
DE = 1
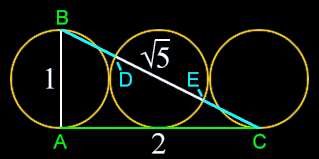
The line BC thus expresses the following embedded phi relationships:
BE = DC = (√5-1)/2+1 = (√5+1)/2 = 1.618 … = Phi
BD = EC = (√5-1)/2 = 0.618… = phi
This simple and elegant way of expressing the most standard mathematical expression of Phi was discovered and contributed by Bengt Erik Erlandsen on 1/11/2006.
Construction by compass and ruler:
Scott Beach developed a way to represent this calculation of phi in a geometric construction:
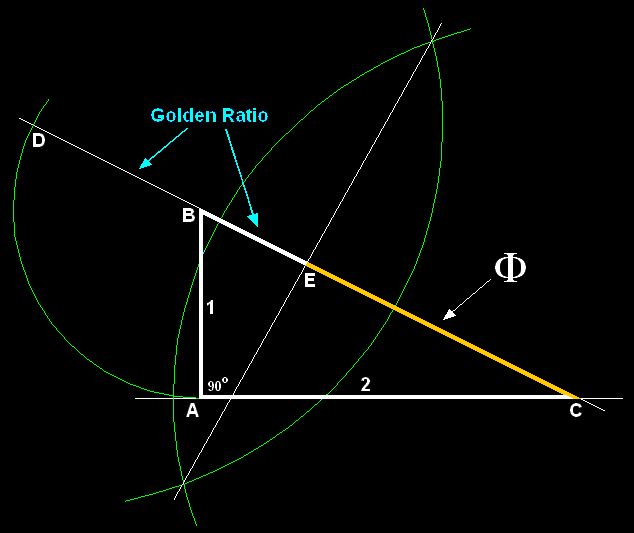
As Scott shares on his web site:
Triangle ABC is a right triangle, where the measure of angle BAC is 90 degrees. The length of side AB is 1 and the length of side AC is 2. The Pythagorean theorem can be used to determine that the length of side BC is the square root of 5. Side BC can be extended by 1 unit of length to establish point D. Line segment DC can then be bisected (divided by 2) to establish point E.
The length of line segment EC is equal to Phi (1.618 …).
The length of line segment DB is 1 and the length of line segment BE is the reciprocal of Phi (0.6180…).
Taken together, DB and BE constitute a graphic representation of the Golden Ratio.



I want the 27/4 something like that formulae
This is a great geometric proof. When you set the diameter of your circle to be Root 5, as the diagonal of the Double Square, and use this knowledge to translate the Phi Formula of (1 + Root 5) divided by 2 into a picture or geometrical construct, you end up with the Maltese Cross-like design worn by royalty and military, but upon closer inspection, if you spun the central circle around in the central square, like a roulette wheel, the locus of this formula, the infinite midpoints of (1 + Root 5) gives a circle, and as we know, Pi is the Circle and Square relationship. This means that Pi is really based on the harmonics of Phi, and leads to the True Value of Pi, (aka JainPi) having a value of 4 divided by the Golden Root of 1.272… giving 3.144…. For more details about this remarkable yet simple discovery, see a 13 page article on my website, under the title of “True Value of Pi, JainPi = 3.144” having this link: http://www.jainmathemagics.com/page/10/default.asp.
Ummm… isn’t ‘true pi’ the one that everyone
agrees is 3.14159265…?
If you want an easy integer fraction to approximate the golden ratio, try 8/5. Or 13/8. Or 21/13. Or 34/21. Or 55/34. Or 6765/4181.
Next time just say “Divide pairs of the Fibonacci sequence.”
+1 or +(√5 + 1)/2
I have discovered two formulas for phi. I have constructed images that show why these formulas are true, but you can also calculate for yourself that these formulas are correct.
I don’t know if other people have also discovered these geometrical truths, but if not, let it be known that Ferry van Haastert was the first 😉
The phi formulas:
phi^3 + phi^2 + phi^3 = phi^5
phi^2 + phi + phi^2 + phi^3 + phi^2 + phi + phi^2 = phi^6
For clearity: phi^2 = phi x phi = phi² = phi squared ; phi^3 i = phi x phi x phi = phi to the third power ; etc etc.
Geometrical construction of the number Phi is very interesting. I am amazed finding the direct relationship of geometrical construction and the most important mathematical numbers. This is wonderful and magical..!!!
INTERESTING!
Pls Ref:
— http://www.stefanides.gr/pdf/2012_Oct/PHOTO_12.pdf
—http://www.stefanides.gr/pdf/BOOK%20_GRSOGF.pdf
—http://www.stefanides.gr/pdf/BOOK_1997.pdf
—https://www.youtube.com/watch?v=XeOjPmKSsOI&feature=em-upload_owner
Regards from Athens,
Panagiotis Stefanides
http://www.stefanides.gr
“Dividing a line into the Golden ratio from the double square – square root of 5 relationship ”:
Any line can be divided into the Golden ratio when a double square rectangle is constructed over that line. Swing an arc with a compass measurement equal to half of the double square rectangle on to the diagonal of the double square rectangle and then swing another arc with compass measurement equal to the larger division of the diagonal of the double square rectangle that is the result of the shorter length of the double square rectangle being subtracted from the diagonal of the double square rectangle on to the longer length of the double square rectangle. The result is that the longer length of the double square rectangle that is also the same as the desired line that is to be divided in to the Golden ratio has now been divided in to the Golden ratio of Cosine (36) multiplied by 2 = 1.618033988749895.
A square is also made from 2 horizontal double square rectangles and also 2 vertical double square rectangles. If the desire is to find the shorter part of the Golden ratio when you have a line and your desire is to make the line longer the use of a square that is divided into half so that the double square rectangle can be used by swinging an arc from the centre edge of the large square with a compass measurement equal to the diagonal of the 2 rectangles that are formed of double squares that also make up the largest square on to the extension of the line. Remember that a square is also made up from 4 smaller squares. The height of a Pentagon can also be found if a Golden rectangle is constructed from the centre of the circle that contains the Pentagon with the shorter edge of the Golden rectangle being equal.
“Numerical formula for dividing a given line into the Golden ratio from the Double square rectangle – Square root of 5 relationship”:
The numerical formula for dividing a line into the Golden ratio from the Double square – square root of 5 relationship can be written as 1 multiplied by the Square root of 5 = 2.23606797749979 subtract 1 = 1.23606797749979. 2 subtract 1.23606797749979 = 0.76393202250021. 1.23606797749979 divided by 0.76393202250021 = The Golden ratio of 1.618033988749896. Also 2 divided by 1.23606797749979 = The Golden ratio of 1.618033988749894.
The Pythagorean theorem can be used to prove that the diagonal of a double square rectangle divided by the shortest length of the double square rectangle is the square root of 5 = 2.23606797749979.
derive the value of phi
given:
ϕ=a/b
One principle of algebra is that solving for more than one variable requires that same number of equations. So to solve for Phi given a and b requires two equations, not just one. The other relationship that we know when solving for phi is that the two line segments in ratio of a/b also add to the entire line segment, and the ratio of the entire line segment to the longer (let’s say it’s a) is the same as a/b. So we know that (a+b)/a=a/b AND that a+b=1. Now we two equations that we can work with to determine the values of a AND b, and therefore the value of a/b. This can be solved with the quadratic formula. See more on this, and the solution here: https://www.goldennumber.net/math/
As √5 on two plus one is to reciprocal √5 on two
A is to B as A plus B is to A
Heres what I was searching for. and what I remember posting maybe ten years ago..
https://www.instructables.com/id/The-Golden-Proportion/
For mpore background, I posted this or these comments here because you have a article concerning the Phi Point on the Earth…. and I was tracking down the power ratios of the true Ark and cube of the Holy of Holies, which also match the {Phi pyramid of Giza and the Kings Chamber ‘s sarcophagus.
I’m into prophecy mainly, as we have the ways and means of beating the dark eyed ones, as told us, by the Lord.
Ha, so with that geometry, and the exact distance of PHI within a 2.5, by 1 by 1 ratioed ark….. or lets say 5 by 3 by 3 ark, was there a 4 ratio within, lets say the Rod of Aaron, that made it powerful by the Shikanan of God above at 5 cubits, or the center of the H.O.H, also called the womb of God, as all creativity stemmed from HIS CREATIVE POWER.
The difference at Mecca, and now Antartica is that the dark side Kur and his ill, want to use a copy, that demonstrated its power in killing at Mecca, in the E.T. Note the False Prophet Kur…. does miracles, in contast and response to our miracle working power and rod of Moses/Aaron.
Rev 11, 12 13 etc..
IE is the rod of Aaron ratioed at 4, making a 5-4-3 triangle within the ARK that draws power…or 2 cubits in length……… seems aweful short, but the rod fits into the ARK and was stored there, so couldnt be a shepherds rod..IMO….
I like math, that has application rather than just math for math sake..especially when applied to the MASTERS MATH, as He is the Great Scientist and Mathematician.
LIJ
David
I’ve gone deep with egyptian mysteries man…..and found the philosopher stone through math in the giza pyramid. I think we need to talk and work with one another because…. i suck at math, and its something i need badly…what you need…is WHAT i have…. the occult training.
Sorry to post again, please remove if necessary.
Anyway the hyper above showed ‘raising the PHI pole, in getting the EXACT length 1.618…..this if raised upwards via a compass arc from the base or ground….. if another construction is made on that plane, it also would create a PHI distance that would then cross the first Phi arc making the cross sectional PHI PYRAMID of Giza (NJ etc..) Its heigth then would be exactly the square root of PHI or 1.272…..
IE, which would mean we have gone from a square or cube to a phi pyramid…… or lets say from the cube of the Holy of Holies to an inner PHI pyramid in the ARK. Geometrically finding exact PHI and exact square root of PHI or the Golden Section… Hmmm through compass and square….
This meaning the PHI spiral up and out of the PHI pyramid could stem from its design of the basic physics of space, a cube. Maybe there is something to its design, that dictates it can be powerful just by its ratios. Maybe in truth it is a Farraday capacitor, as some speculated, but forget Farraday if it a truth, it would be the Lords capacitor.
Ill find, the Ark of Gabriel web site, but I reckon anyone can find it easy enough
ATBIH
David
http://www.stefanides.gr/pdf/2012_Oct/PHOTO_12.pdf
http://www.stefanides.gr