A new fundamental geometric shape with a relationship to Phi.
Here’s a challenge to “all the real mathematicians in the back row,” as my college professor often said:
- Picture the classic solids of geometry, each sitting inside a cube that encloses it on all sides. What is the ratio of surface area of this tangent cube to the surface area of the solid, and which solid results in a ratio that is within 1% of phi?
- Which solid has a silhouette projection from the x, y and z axes of a cube, a sphere and a convex parallelogram?
Give up? Enter the DOR (the Direct Opposite Reverse), at TheDOR.net, a geometric solid discovered by David P. Sterner that is the answer to both of these questions. Sterner sees the DOR as the missing geometric link, a new shape in geometry’s basic set of solids (cubes, cones and cylinders, etc.) that haven’t had a new member since the time of Euclid before 200 B.C.

The patented refractor lens of the DOR creates images that when printed directly to photographic paper create two opposite images, the normal inverse image created by any convex lens but also a positive image of the original subject matter in its true orientation.
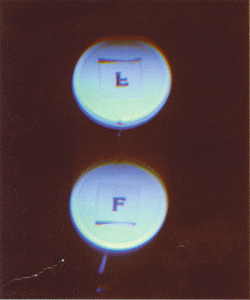
The images photographed through the DOR also have an appearance of depth:

You can construct your own 3D model of the DOR using the template below, which is available in a DOR template PDF download.
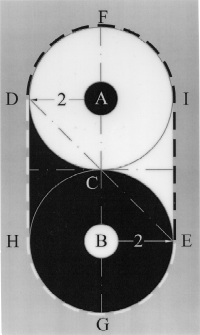 |  |
When constructed, the model has these views:
| Circle / Sphere view | Square / Cube view |
 |  |
| Third / Convex view | 3D view of all three |
 |  |
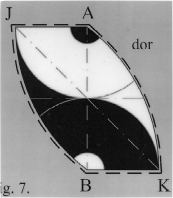
Now picture the various geometric solids sitting inside a tangent cube, that is a cube to which all sides of the solid are touching. The area of the solid to the area of its tangent cube is below, and only the DOR is close to phi, 0.618. Can anyone create a solid as simple in construction but with a tangent cube that is as close to phi, or closer yet? If so, contact David Sterner with your discovery.
| Solid | Solid Image | Surface Area Formula of Solid | Ratio of Surface Area of Solid to its Tangent Cube |
| DOR |  |
0.6086903 | |
| Cone | 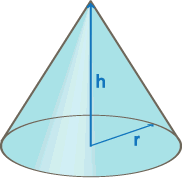 |
pr² + p( r x s )wheres = √( r² + h² ) | 0.4236003… |
| Dodecahedron | 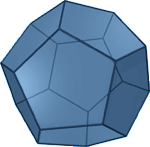 |
3a² Ö(25+10Ö5)where a = length of an edge, with a width of two times phi and edge of 2/phi. | 0.50202854 |
| Pyramid | 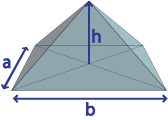 |
(½ x P x s ) + A where A = area of the base shape P = perimeter of base shape s = height of face triangles |
0.5393446… |
| Sphere | 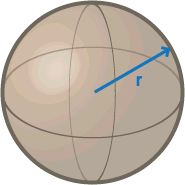 |
4pr² | 0.5235987… |
| Cylinder | 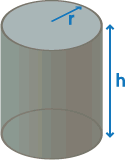 |
2pr² + 2prh | 0.7853981… |
| Prism | 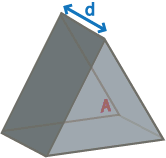 |
2A + Pdwhere A = area of the base shape P = perimeter of base shape d = height of prism |
1.0000000 |


This is my first day looking arround for the golden ratio. I want to relate it to the pentagon to a circle. I was looking at your shape and maybe the 0.01 difference in your shape could be consumed in the creation of matter to make the shape itself. IE the point of blending?
Anyway have a good day.
As to the pentagon and the golden ratio, see also the Geometry page. PhiMatrix golden ratio design software also has a template for pentagons and pentagrams.
Mind blown!
fascinating stuff, thanks for making it an open source !
The day has come for the light and truth of why this has come to surface .
Thank you me sterner for your belief and hard work and determination to make this known ..you are a hero to me and many others.
Truly an inspirational discovery and fascinating bit of geometry. Like no other shape I’ve seen.
To fulfil requirement 1:
Just take a Rhombicuboctahedron, which belongs to the Archimedean solid. You will find a ratio of the surface area of the Rhombicuboctahedron to its tangent cube of 0.613776, which is very near to the golden ratio. The required formulas can be found on https://en.wikipedia.org/wiki/Rhombicuboctahedron.
I think it is rather easy to construct a solid, whose surface is the golden ratio of the tangent cube. Just take a cube and cut away slices from its edges, until the golden ratio is obtained. Also, you take a cylinder a round its edges, until the golden ratio is obtained.
Requirement 2 is from a mathematical point of view not very precise, because a “convex parallelogram” may cover a lot of different shapes.
I am an old friend of Davids and saw this when he first invented it.
would you be willing to send me an email? I’d love to hear more about the lens he created and what it first looked like. jordanzothegreat@gmail.com
Well David I believe is possible to make a solid piece not that big but like a piece of mirror one piece is a mirror n the other one the formula black n white ?