Phi, Φ, 1.618…, has two properties that make it unique among all numbers.
- If you square Phi, you get a number exactly 1 greater than itself: 2.618…, or
Φ² = Φ + 1.
- If you divide Phi into 1 to get its reciprocal, you get a number exactly 1 less than itself: 0.618…, or
1 / Φ = Φ – 1.
These relationships are derived from the dividing a line at its golden section point, the point at which the ratio of the line (A) to the larger section (B) is the same as the ratio of the larger section (B) to the smaller section (C).

This relationship is expressed mathematically as:
A = B + C, and
A / B = B / C.
Solving for A, which on both sides give us this:
B + C = B²/C
Let’s say that C is 1 so we can determine the relative dimensions of the line segments. Now we simply have this:
B + 1 = B²
This can be rearranged as:
B² – B – 1 = 0
Note the various ways that this equation can be rearranged to express the relationship of the line segments, and also Phi’s unique properties:
B2 = B + 1
1 / B = B – 1
B2 – B1 – B0 = 0
Note: Bx means n raised to the x power. Some browsers may not display exponents as superscripts or raised characters.
Now we have a formula that can be solved using the Quadratic formula. This formula allows you to solve a quadratic equation for an unknown x, with a, b, and c as constants. A quadratic equation has this form:
-
ax² + bx + c = 0
The solution to this is found with the quadratic formula:
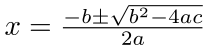
So our formula for the golden ratio above (B2 – B1 – B0 = 0) can be expressed as this:
1a2 – 1b1 – 1c = 0
The solution to this equation using the quadratic formula is (1 plus or minus the square root of 5) divided by 2:
( 1 + √5 ) / 2 = 1.6180339… = Φ
( 1 – √5 ) / 2 = -0.6180339… = -Φ
The reciprocal of Phi (denoted with an upper case P), is known often as by phi (spelled with a lower case p).
Phi, curiously, can also be expressed all in fives as:
5 ^ .5 * .5 + .5 = Φ
This provides a great, simple way to compute phi on a calculator or spreadsheet!
Here’s a little more phi mathemagic, contributed by Abe Ihmeari:
Φ * √5 = 3.6180339… = Φ + 2
Determining the nth number of the Fibonacci series
You can use phi to compute the nth number in the Fibonacci series (fn):
fn = Φ n / 5½
As an example, the 40th number in the Fibonacci series is 102,334,155, which can be computed as:
f40 = Φ 40 / 5½ = 102,334,155
This method actually provides an estimate which always rounds to the correct Fibonacci number.
You can compute any number of the Fibonacci series (fn) exactly with a little more work:
fn = [ Φ n – (1-Φ)n ] / √5
Note: √5 can be expressed as 2Φ-1 to use Φ for all the terms above.
Determining Phi with Trigonometry and Limits
![]()
Phi can be related to e, the base of natural logs,
through the inverse hyperbolic sine function:
Φ = e ^ asinh(.5)
It can be expressed as a limit:
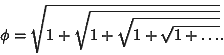
or

Other unusual phi relationships
There are many unusual relationships in the Fibonacci series. For example, for any three numbers in the series Φ(n-1), Φ(n) and Φ(n+1), the following relationship exists:
Φ(n-1) * Φ(n+1) = Φ(n)2 – (-1)n
( e.g., 3*8 = 52-1 or 5*13=82+1 )
Here’s another:
Every nth Fibonacci number is a multiple of Phi(n),
where Phi(n) is the nth number of the Fibonacci sequence.
Given 0, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987, 1597, 2584, 4181, 6765, 10946
(Every 3rd number., e.g., 2, 8, 34, 144, is a multiple of Phi(3), which is 2)
(Every 4th number, e.g., 3, 21, 144 and 987, is a multiple of Phi(4), which is 3)
(Every 5th number, e.g., 5, 55, 610, and 6765, is a multiple of Phi(5), which is 5)
(Every 6th number, e.g., 8, 144, 2584, is a multiple of Phi(6), which is 8)
(Every 7th number, e.g., 13, 377, 10946, is a multiple of Phi(7), which is 13)
And, as contributed by Abe Ihmeari, for any Fibonacci sequence number f(n), we find that f(n)-f(n-5)-f(n-10) = 10 ∙ f(n-5). This is easiest to see when the Fibonacci sequence numbers are grouped in fives. As an example, 4181-377-34 = 3770, which is 10 ∙ 377, and 28657-2584-233 = 25840, which is 10 ∙ 2584!
| 0 | 5 | 55 | 610 | 6765 |
| 1 | 8 | 89 | 987 | 10946 |
| 1 | 13 | 144 | 1597 | 17711 |
| 2 | 21 | 233 | 2584 | 28657 |
| 3 | 34 | 377 | 4181 | 46368 |
And another:
The first perfect square in the Fibonacci series, 144,
is number 12 in the series and its square root is 12!
0, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144
or, if not starting with 0:
1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144



We should develop a logical system based on powers of phi to define itself.
if you start with φ^-∞ for zero state. Next φ^-2 would be useful to add to φ and φ^2 to get 2 and 3. With zero power you have 1 together with 0,2,3 whole numbers represented in endless possible combinations of powers of φ. Each combination could represent a different set of logic. I am only barely grasping what kind of operations would be possible in virtual machine code! With a base of φ…
Your logical systems resembles that of Godel on the primes for p>p, where the series is 2,3,5,7 taken in powers representing characters, such that p=0,>=1. The 2^0 * 3^1 * 5^0 = 1*3*1 = 3, which is a prime representing p>p. To do the same on the Fibonacci series 0,1,1,2 …. 0^1 * 1^1 *1^0 = 0*1*1= 0
If you divide phi into 1, you get a number exactly 1 less than phi: 0.61804…:
1 / Phi = Phi – 1 = 0.3 + 1/pi = 1.61804 – 1 = 0.3 + 0.318..
1/Phi – 1/pi = 0.3 For example 34/55 = 0.6181818181818182…, 34 and 35 are Fibonacci numbers; 1/pi = 7/22 = 0.3181818181818182, which difference is 0.3; and 34/55 – 7/22 = 1/11 *(34/5 -7/2) = 1/11 * (68 – 35)/10 = 33/11 * 1/10 = 0.3
Even though I agree that recursion is not the right way to find a Fibonacci number, I have to say using it to teach recursion is a good idea. Because its simple. Easy to get the concept thru this example.The most common real world application for recursion is to walk thru a tree structure. That example will be complicated. Also you will have to have an understanding of trees and stuff before hand.Then again, there may be a simple, but real world example that I’m not yet aware of. If someone knows of one, let me know.
Human brain
You mean like ‘i’?
It would be very interesting.
1 Vesica Pisces on Axis 1 = 1
1 Vesica Pisces on Axis 2 = Square Root of 5
2 Vesica Pisces on Axis 3 = 2
Axis 1 is measured by the radius of the center to the circumference of a circle
Axis 2 is measured by the center to center of two flower of life circles.
Axis 3 is measured by the point where axis 1 penetrates the circular form and to the center of the adjacent circle (along axis 2)
yeah
I’m DDSharma, creator of physics of Thoughtonics, find golden ratio useful in my theory.
First of all i would like to thank and appreciate you for this tremendous work and the content you have used in this site.
but can you please tell me the logic behind the series given below?…………here is the series
2 3 8 21 55
The series you list is part of the Fibonacci series, in which each number is the sum of the two before it. In the case of your particular series the logic appears to be that you ignore every other result, i.e., the 5, 13 and 34. Another way of getting to the same result is to use this logic: 2+3+8*2=21 and 3+8+21*2=55 so the next number in the series should be 8+21+55*2=139.
I believe, though I could be wrong, that you made a mistake in the sequence
3+8+21*2=55 therefore 3 + 8 + (21 x 2) = 11 + 42 = 53 not 55
this sequence that guarav has listed includes all the numbers not just the last three.
so you need to include the 2 of the first number to get 55 so the next number would be
2 + 3 + 8 +21 + 2(55) = 144
2 + 3 + 8 + 21 + 55 + 2(144) = 377
2 + 3 + 8 + 21 + 55 + 2(377) = 843
oops the last line should include 144
2 + 3 + 8 + 21 + 55 + 144 + 2(377) = 987
sorry got ahead of myself
I don’t know what the relation is, but, when adding up all the missing digits, starting from 0 phi sequence we have 0+1+5+13+34+89+233= 375
Or the 1 phi sequence 1+1+5+13+34+89+233=376
But no matter where you go in the sequence adding the skipped numbers will always produce an integer of phi(n) -1 or phi(n) -2 depending on how the sequence is assumed to start.
The 0 sequence seems to be phi(n+1) is Fibonacci 2,3, then skipping every other number in the sequence to phi(n) + (all the skipped numbers + phi^2 + (-1/phi))
The 1 sequence ends instead with phi +(-1/phi) if we are adding two 1’s as missing.
Probably overthinking it, I don’t understand an expression or formula for it. Maybe just coincident.
Mr. Meisner,
Has anyone noticed that
(PHI + PI) Tanh= 1
I’d like to understand that better with graphics.
Can you explain the statement (PHI + PI) Tanh = 1
Next in the series is 144.
like it
F(n+1) = [ sum of series till F(n-1) ] + [(2*F(n) ]
Suppose F(n) is 55
Then
=(2+3+8+21) + (2*55)
F(n+1) =144
F(n+2) =(2+3+8+21+55) +(2*144)
=89+288=377
So on..
The series is actually 1 1 2 3 5 8 13 21 34 55 89 144 233 377 610 987 1597…………..
This is Fibonacci series.
For 2 3 8 21 55
#2+3(2)=8
#3+8(2)=19
so this is not a perfect sequence.
The sequence should include 5 13 34 for a complete list.
this is very helpful
How do you know all of this math (golden number)? I’m in the 8 grade i want to learn this. How do I get help?
I can help! I am also in the 8th grade, and have developed an unhealthy obsession with this lovely number.
Phi is commonly expressed as a ratio; if you imagine that the longer portion of the following line is 1.618, or Phi, and the shorter section is one (following the ratio 1.618/1), then you get a visual representation of the golden ratio:
|————-|——–|
a b
a/b = a+b/a
This might be a little confusing, but bear with me! The Fibonacci Sequence is the crazy relative of Phi. It starts with the numbers 1 and 1 and then progresses as follows:
1, 1, 2, 3, 5, 8, 13…
Now for the pattern! Adding 1 + 1 = 2, right? Now, if you add 1 + 2, you get 3. 2 + 3 = 5. To find a number of the sequence, you add the two previous numbers. So, to find the next one of my example sequence, you would add 8 and 13 to get 21. Which will then get you to 13 + 21 = 34.
If you quickly google Fibonacci Sequence, you will find a great visual depiction of this series. To give another example of Phi in use: a golden rectangle, which can be found in many architectural projects, has a height of 1 and a length of 1.618. The human face has at least 30 different representations of the golden ratio in it. Sunflower seeds grow in a Fibonacci Spiral pattern from the center of the flower. The examples are endless!
If you have any more questions (or maybe want some real pictures, as it’s a little hard to grasp the concept with no visual aid), you can contact me at: lalah.sander@gmail.com.
I hope this helps!
DAMN WTF BRO IM IN 11th GRADE AND I JUST DISCOVER IT NOW BECAUSE I WAS PLAYING WITH ALT COMBNATION WITH NUMPAD AND I CREATED THIS SYMBOL AND I SEARCH IT AND GOT HERE CAN YOU EXPLAIN TO ME WHAT IS IT HAHAHA I DONT EVEN UNDERSTAND THIS BUT I KNOW ITS OMNIPOTENT
I want to know what is the englis equivalent word of greek word ‘phi’
Phi is a letter of the Greek alphabet, so its closest English equivalent is the letter F. Phi was chosen to represent the golden ratio to recognize the Greek sculptor Phidias, who lived from about 480 – 430 BC. He is regarded as one of the greatest sculptors of classical Greece. His statue of Zeus at Olympia was one of the Seven Wonders of the Ancient World. He also designed the statues of the goddess Athena on the Athenian Acropolis. Mark Barr, a mathematician, first used the Greek letter phi (Φ) to designate the golden ratio. See the Golden Ratio History page for more.
I learned how the square root of 1 plus the square root of 1 plus square root of 1… etc.
if you let x=squareroot(1+squareroot(1+squareroot(1…))) then square both sides you get
x^2 = 1 + squareroot(1+squareroot(1+square root(1….)))
then substitute x in for the squareroot(1+…)
x^2=1+x
then subtract both sides by (1+x) to get
x^2-x-1 = 0
Then use the quadratic formula
x=(1 +/- squareroot((-1)^2 – 2*(1)*(-1)))/(2*1)
Clean everything up to get:
x= (1 +/- squareroot(5))/2
Take the positive outcome, and get phi!!
Thank you.
Φ^n = F(n)*Φ + F(n-1)
When F(n) is the “n”th Fibonacci number (n≠1, obviously)
Has anyone else noticed this?
This family of equations has other solutions besides phi, (i.e. (1-sqrt5)/2 and complex numbers) but phi is a solution for all of them, and also the only positive solution for any of them.
Hi Peter,
yes, I found this, too.
And you mentioned the second root of eq. n^2 – n – 1 = 0: let’s call it phi (small phi, it is < 0)
Here is another nice recursion for Fibonacci, using Phi and phi:
F[n] = Phi^(n-1) + phi * F[n-1]
Have fun!
I’m in 10th grade and doing my math project on phi. Can anyone give me a few more, preferably simple, interesting things about phi in math? I need to explain it to people who’ve never heard of it before. Please reply by 5th July
Check out the Phi Basics and Geometry pages for some practical and visual applications.
How do you show that [1+√5/2][1+√5/2]= [1+√5/2]+1. I’ve tried it in so many ways but I never make it equal.. Help..
Hi Jessica,
The proof you are looking for is as follows;-
(1 + √5)/2 * (1 + √5)/2 = ((1 + √5) * (1 + √5)) /4
= (1 + 2*√5 +5) /4
= (6 + 2*√5) /4
= (6 + 2*√5)/4 – 4/4 + 4/4
= (6 + 2*√5 – 4)/4 + 1
= (2 + 2*√5) /4 + 1
= (1 + √5) /2 + 1
Cheers,
Ted.
Also if anyone’s interested here is the proof of Φ = 1/Φ + 1 ;-
Since Φ = (1 + √5) / 2
Then, if Φ = 1/Φ + 1, it follows that;-
(1 + √5) / 2 = 2/(1 + √5) +1
= 2/(1 + √5) + (1 + √5)/(1 + √5)
= (2+ 1 + √5)/(1 + √5)
= (3 + √5)/(1 + √5)
= (3 + √5)/(1 + √5) * 1
= (3 + √5)/(1 + √5) * (2/(1 + √5))/(2/(1 + √5))
= ((3 + √5) * (2/(1 + √5))) / ((1 + √5) * (2/(1 + √5)))
= ((6 + 2√5) / (1+√5)) / 2
= ((1 + √5)^2) / (1+√5)) / 2
= (1 + √5) / 2
Therefore Φ = 1/Φ + 1
Regards,
Ted Krapkat
I’ve just started down this path, I’m excited. Carroll’s “curiouser and curiouser” keep popping into my head
I have become very familiar with this number and its uses sense I stumbled across it a year ago, in fact, it has literally changed my entire out look of the bible, and I wish to include the information found in this web site in a book I am writing about the bible and its patterns, and this numbers and its variations appear so often that its quite spooky.
Jack, since you’re going to write a book, it’s ‘since’ not “sense”. Does that make sense ?
So umm… I didn’t see this anywhere on the page, but for any number in the sequence… determining the next number is just a matter of multiplying the current number by Phi and rounding it… (after the pair of 1s, mind you).
I have found design drawing of pyramid by the fractal perspective based on the legendary theory of the circle. square and triangle the first in the world.
It would be correct answers for your questions.
My point of view, now humankind is backward mentally and physically since 11,000years ago.
There are a lot of new knowledge and special information that humankind must know the fact such as
1) Origin of alphabets
2) Origin of numbers
3) Origin of languages
4) Origin of civilization
5) Mono-genesis species
6) The moving theory of the axis of the earth
7) Origin of trigonometry
8) Origin of equation
9) Origin of integration
10) Origin of differentiation
11) Origin of coordinates
12) Origin of STEM
13) Origin of origin etc much more
The pyramid of time capsule was a historical civilization.
I have few evidence.
For more information, http://www.linkedIn.com or http://www.cndreams.com etc.
How do you show that phi^n = F_n * {phi} + F_{n-1} ??
Thank you.
use equation x squared-xy-y squared to show that x over y is = phi
I have come across this equation called the fibonacci activation function. How it it derived and how it it related to the golden ratio?
Phi(y) = ((sqrt(5) – 1)y^3)/2 + ((3 – sqrt(5))y^5)/2
Golden ratio: for any segment c, find a and b segments – YouTube http://youtu.be/cp3dpvqns_4
Golden ratio Phi Space – YouTube http://youtu.be/JLzX2XxSVgs
i hear—because i have a spiral cochlea
doesn’t mean i understand–that takes
a mind willing
i honestly believe there’s a solution and
if i look-i have a chance of finding
and that’s my truth 🙂
I need significance of phi equation
The significance of the equation, ( 1 + √5 ) / 2 = 1.6180339… = Φ, is that this gives the value of the relationship that appears when dividing a line such that the ratio of the entire line to the larger segments is the same as the larger segment to the smaller segment. This dividing is the golden ratio that appears extensively in mathematics, geometry and nature. It has thus also been applied to the design arts to achieve a natural appearance in composition and to enhance aesthetics.
We – the human species -, and in relation to Phi, is in need of a Mathematician for an altruistic job. There is a unique pattern always applied by Nature when organizing matter/energy into a working complete system. This pattern is built by the process of life cycle. You know, it is about the phenomena that makes our bodies – as systems – born,glow,mature,degeneration,death – when our bodies changes its shapes all time. So, using this process of life cycle Nature has created systems, from atoms to galaxies to cells to human bodies. How? Nature build an inanimate object body from any nebulae, or dust. Then Nature applies the force upon several inanimate objects of same shape/constitution, which will have their shapes, functions, changed into new shapes. When Nature gets 6 different shapes from that kind of object, it arranges the shapes in a linear sequence. But the location of each object must obeys the sequence of life cycle ( birth,grow,maturation,etc.). As the shape of your body known as teenage has as left neighbor the shape of kid and as the right neighbor the shape of adult ( so, there is a link about time, etc., between neighbors) and the natural tendency of neighbors to keep together, the different objects are aligned mimicking the life cycle sequence, which creates links between them and finally, a running circuit. The system is ready.
We make no idea how this knowledge is important for us to make the word a better place for everybody. this is the natural principle of automation productive process, reproduction, life, etc.
I got the metaphorical representation of all these process into a working system as a formula, em shape of software diagram. With this formula I am understanding every natural and event phenomena from a very interesting new perspective. But, we need to learn how to reproduce this formula as material tools for practical applications. And for making plans, strategies, creating new systems, etc. I am merely a naturalist philosopher observing Nature in the Amazon jungle, with no knowledge of modern technology, complex Math. We need to find a way for representing the formula as an equation. That’s why we are in need of a Mathematician that grasp something of this new idea and trying to find the equation. my research job is not profitable, I am selling nothing ( only spending), it is merely altruistic, so, I can’t hiring a Mathematician, but, if the mathematical equation based on the formula gets some donations, by sure, we will share it half and half. Someone there?…
My head hurts.
I haven’t figured out math notation on a computer yet. Let X = arccosine of the reciprocal of phi. Y = sine of one half X. Phi mutiplied by the reciprocal of y is the square root of two, precisely.
I am confused which one is capital Phi and which one is lowercase phi. in other websites, the lowercase phi is said to have been assigned to the golden ration.
I understand your confusion, and I’ve been studying this topic for over twenty years. I’ve seen the usages of upper and lower case phi in conflict in varying sources, and it’s not clear who or which body gets to define what is standard or correct. Earlier sources seemed to most often used upper case phi, but more recently the shift is towards lower case phi. As Wikipedia states, “The Greek letter phi symbolizes the golden ratio. Usually, the lowercase form (φ or φ) is used. Sometimes the uppercase form is used for the reciprocal of the golden ratio, 1/φ.” The source for this is shown as ” Weisstein, Eric W. “Golden Ratio Conjugate” MathWorld. I emailed him years back asking to know his source, but never received a response. Po-tay-to, po-tah-to?
Can anyone explain to me how, at the start of the Fibonacci series, we get from zero to one? Okay, I get it that the two previous numbers are added together to get the next one in the series, but why did we add 1 to 0 to kick it off? If we started with nothing (i. e. emptiness or non-existence) where did the “one” suddenly appear from? Looking at it on a cosmic scale, it seems similar to the explanation of the big-bang theory: “first there was nothing, and then it exploded.”
some people skip 0 and 1.
1 + 0 = 1
Thoughtonics says a super- verse got biggest crunch to be Shunyat ie. Zerot which is zero thought and that starts new. Super-verse.
yes, but, if we assume Phi(n) is equal to the distance of the centre of two flower of life circles, axis 12 Vesica Pisces must be equal to (1x-√5)/(2^1/2)ª. This is also proof that Φ = 1/Φ + 1 and also brings to light the significance of Φ in aesthetics.
Thoughtonics says that one P(1) gives 1, two P(1) give 2, three give 3/2, four give 5/3, five give 8/5….. All members of golden ratio
Golden ratio is pretty useful in my theoretical physics viz Thoughtonics. I need to learn it’s all details.
1 1 2 3 5 8 13 21 34 55 89 144 233 377 610 987 1597
1/1=1
2/1=2
3/2=1.5
5/3=1.666
8/5=1.6
13/8=1.625
21/13=1.61538
This is indeed a very complex equation in trying to describe the nonlinear construction and behavior of the Cosmos. Phi is a nonlinearly derived number in base ten arithmetic. The thing to do is to translate it into various number systems; perhaps to the Mayan system of counting in base 5 and 20 or the Ethiopian base 13 system….
I know this is years late, but the topic was already thousands of years old when this was written, so I think I’m good 😁.
There’s an error in the text of the derivation.
The rearranged derivation is down to
B² – B – 1 = 0
Then the reader is introduced to a quadratic equation
ax² + bx + c = 0
But then this substitution is given as the formula for the golden ratio, which is now no longer a quadratic equation in one variable.
1a² – 1b¹ – 1c = 0
I assume what was meant was this:
aB² + bB + c = 0, where a=1, b=-1, and c=-1