Squaring the Circle comes within four decimal places using the Golden Ratio.
Even before the foundations of the Great Pyramids were laid men have tried to “square the circle.” That is, in a finite number of steps, construct a square and a circle that are precisely equal in area using only the most primitive instruments; namely, an unmarked compass & straightedge. Some of the greatest men in all of history have attempted to solve this ancient riddle. They have included mathematicians, architects, politicians, artists, musicians, philosophers, astronomers and theologians.
The task was finally “proven impossible” in 1882 when Lindemann showed that pi was a transcendental number. In other words, it cannot be calculated as the root of a polynomial equation with rational coeffecients. Hence, the decimal values of pi are infinite, and since it is not possible to construct the square root of an infinite number, it is therefore “impossible” to square the circle with exact precision. One can only hope to come close.
Christopher Ricci has recently discovered an elegant method which comes about as close as it gets. The technique is extraordinary in that it employs a royal parade of three successive Phi constructions that ultimately converge on the same ratio attained by the well known equation: Phi Squared/5 = Pi/6. The procedure is outlined below.
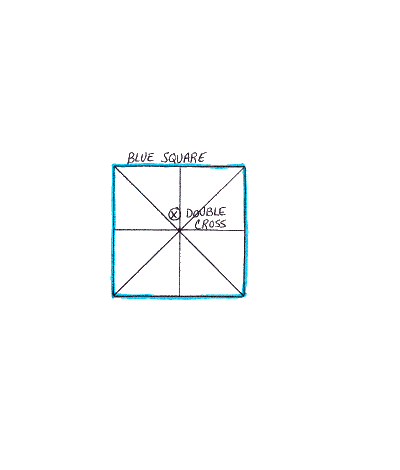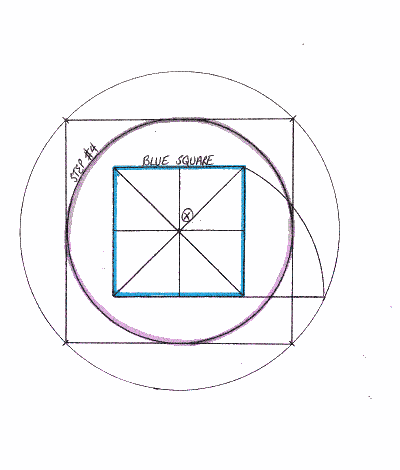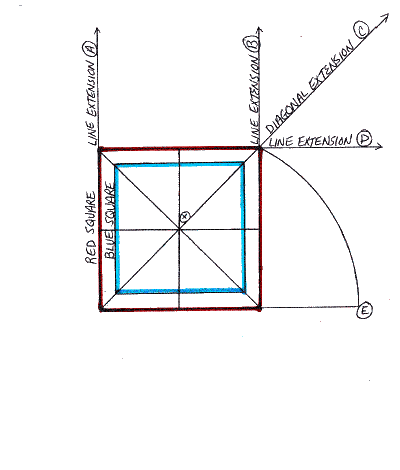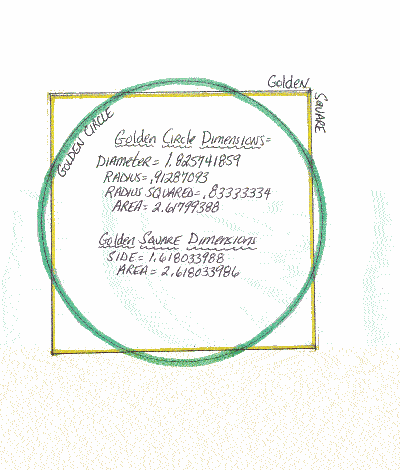
Download the Squaring the Circle with the Golden Ratio pdf file or visit The Circle is Squared to explore the steps at your own leisure.
If we consider the Red Square as a unit square (Side = 1; Area = 1), the following calculations will result:
Golden Square: Side = Phi (1.618033988); Area = Phi Squared (2.618033986).
Golden Circle: Radius = (0.91287093); Radius Squared = (.833333334). Area = (2.61799388).
With respect to the area, there is virtually no difference between these two shapes. Measured in inches the difference is literally microscopic. And even if we convert them into square feet, the difference would remain undetectable by the naked eye. The area of the Golden Circle subtracted from the area of the Golden Square would be a miniscule .0057751 square inches. Converted to metric = a little over 144 sq. microns. This would enclose an area of 12.111 X 12.111 microns; which is roughly the size of two red blood cells.
As far as linear measurement is concerned, this construction yields a very tight approximation for pi as well; (3.141640784). [Note: The math for this is located on Figure #13 in the pdf file]. This is 99.85% accurate for true pi. To illustrate just how significant this is we would need to enlarge the shapes astronomically. Imagine, for example, you have a planet with a diameter of a thousand miles. According to pi it would take a car racing along at 60 mph more than 52 hours & 21 minutes to circumnavigate the globe at its equator. If we were to extrapolate our travel time using Phi instead, the difference between the two times would be less than three seconds! Now that’s impressive no matter how you slice it.
The fact that we can attain such a high degree of precision without the aid of modern tools and in so few steps sets this construction apart from some of even the most ingenious techniques. If you have any comments or would like to discuss this further with Chris, you may contact him at Ricci1.1107207@yahoo.com
Thanks go to for Chris Ricci for his passion and dedication in developing this innovative response to a classic geometric challenge, finding another way to relate phi to pi and for sharing it first with GoldenNumber.net.



Very interesting “Squaring the Circle with Phi “.
I am attaching my links using a special triangle [ the quadrature triangle ]
and further theorems invented for the case:
http://www.stefanides.gr/Html/QuadCirc.htm
http://www.stefanides.gr/Html/piquad.htm
http://www.stefanides.gr/Html/theo_circle.htm
http://www.stefanides.gr/Html/platostriangle.htm
http://www.stefanides.gr/pdf/BOOK%20_GRSOGF.pdf
Any comments will be appreciated
Regards from Athens,
Panagiotis Stefanides
——————————
panamars@otenet.gr
I just wanted to pass along my new email address & a link to my new website dealing with the subject of squaring the circle with the Golden Ratio.
Read and see for yourself: squaring the circle is resolved!
I found in 2001 in the drawing of ‘Vitruvian Man’ the Quadrature of the Circle according to Leonardo da Vinci. You can see:
After reading this, I realized that I had the basis for an alternate solution to squaring the circle using the golden ratio.
http://flic.kr/p/ebMFMt
A new geometry design, offering conceptual proof that only three points are required to square the circle. When the green scalene triangle is created, the length of the horizontal line equates to the square root of Pi:
http://aitnaru.org/threepoints.html
(large circle’s diameter = 2000000 units)
Re: http://www.aitnaru.org/images/Pi_Corral.pdf
Or consider the “Pivotal Confirmation?” design that shows how two right triangles in a squared circle can pivot 90 degrees and still retain the same hypotenuse (side of an inscribed square).
A colorful drawing and concise review of the current research plateau:
http://www.aitnaru.org/images/Pi_Corral.pdf (see design: Impossible Balance)
“Quick Guide for square Pi” – Simple display of geometric balance in a squared circle.
The circle (D = 2,000,000 units) is drawn next to last, confirming the starting object: a green perpendicular line set, representing the square root of Pi (1,772,453.850.. units) and half the square root of Pi (886,226.925..).
The circle is drawn via a perpendicular line set (magenta, perpendicular line not shown). The mid-point distance of the two magenta lines is known when the first object is drawn. When rotated to the precise point on the circle, these lines have length equal to the side of a square inscribed in the golden circle.
Of course, “stuff” happens along the way but can be guessed from the starting geometry. The red lines, drawn last, confirm all of the good stuff that happened.
Why “Impossible”? This is not a solution but contemplation of proof …
and geometrically supportive of the whimsical perspective:
“To square the circle, one must circle the square.”
Continuing research …
Re: http://aitnaru.org/threepoints.html (a Square One conundrum)
Perhaps, the circle cannot be squared (according to the Greek rules) but a squared circle might be proven geometrically:
In the Square One design on this web page, the green scalene triangle (part of the larger isosceles right triangle) contains a 45-degree angle and, theoretically, a base length equal to the square root of Pi. If the circle is squared, the left diagonal side (one end of this red line is attached to the Pi line) must have length equal to a side of a square inscribed in the primary circle.
And for the square root of Pi, only one diameter provides this exact side length: a circle having a diameter of 2. That Pi is an irrational number is insignificant since the lines in the scalene triangle are complementary (perfectly balance the irrationality of Pi).
As you have another paper by Miles Mathis on site I thought that I would post a link to his paper on Squaring the Circle too.
http://milesmathis.com/square.html
Outstanding, heartiest congratulations to Chris Ricci. As a retired architect and devout practising geometrician my fascination with patterning and mathematics has led to this site. The paradoxical impossibility of squaring the circle yet doing so with such elegance and practical accuracy is a wonderful delight. Thank you so much for sharing this fine work.
Thank you so much Mr. Perk Cartel for your gracious comments. I was wondering if you have had the opportunity to peruse the attached website for further details… http://www.circleissquared.com
In it I demonstrate how to “square the circle” PRECISELY with only compass & straightedge on Riemannian manifolds. I think you might find it intriguing. Any feedback you may have to offer would be most appreciated. Again, thank you.
Kindest regards,
C. Ricci
What would happen if someone actually succeeded in squaring the circle to infinite precision? Would he be assassinated? I know you’re going to say it’s impossible. My point is: hypothetically, what if someone actually did it?
He did not get to let anyone know. Anyone who knows the secret, was already known to the amalgam of infinite and finite with such precision he did not get to be born and remains pivoted between the confines of the “Squared Circle” waiting for you to contact him? Had any luck yet then? RDR
http://www.stefanides.gr/pdf/2012_Oct/PHOTO_09_PCST_GEOMETRY.pdf
http://www.stefanides.gr/pdf/D=5,083FOUR_1.pdf
funny that you have a slightly different result for the decimal part of phi and phi squared… considering that all phi is is the number x such that x+1 = x^2. so if phi is 1.618033988 then phi squared is 2.618033988 not 1.618033986. i assume you plugged it into a calculator which is funny considering we are on goldennumber.net and phi squared = phi+1 is the essence of what the golden number is.
Good observation. This article was contributed by Chris Ricci, so you can contact him at the email address provided for clarification.
When squaring phi using a calculator your result will always fall short of phi + 1 because phi is an infinite series. In fact, using 1.618033988 as a value for phi is itself, an approximation (rounded down) since the decimal values go on indefinitely; hence, your result is lower than phi + 1… If you square 1.618033989 (the value of phi rounded up) you will get 2.61803399 (which is too high). It all will depend upon the number of digits your calculator can handle. If you take phi to more decimal places, say 1.618033988749894, the result will be much closer to phi + 1… (but still a tad lower)… Phi could be calculated to a trillion decimal places & it will still fall shy of the mark. But the more decimal places you add, the higher your result will be, and the closer your result will be, until it ultimately converges on phi + 1.. This is a moot point here. If I had used 2.618033988 in my calculations the value would be incorrect.
A year later and still runnin’ in squared circles, but this geometry is certain:
A right triangle with hypotenuse/long_side ratio of 2(sqrt(1/Pi)), where hypotenuse is the circle’s diameter and long side has length equal to a side of the circle’s square, is a circle-squaring object!
Further, 2(sqrt(1/Pi)) can be used to find the ratio of the length of the long side to the short side: 1.9130583802711007947403078280203.., a constant permitting construction of a “golden rectangle”.
Research hinting that squared circles can exist even when they cannot be constructed?
2(sqrt(1/Pi)) = 1.1283791670955125738961589031215..
Harry Lear claims to have found the true value of pi, which should be 3,1446….
http://measuringpisquaringphi.com/
Point G is one of the intersection points of the square of the circle:
https://i.imgur.com/6lKRhpN.png
http://www.stefanides.gr/pdf/2012_Oct/PHOTO_12.pdf
© Copyright 2017 – 2018- 2019, Eur Ing Panagiotis Chr. Stefanides BSc(Eng)Lon(Hons) MSc(Eng)NTUA TCG CEng MIET
https://www.linkedin.com/pulse/generator-polyhedron-platonic-eucleidean-solids-panagiotis-stefanides/
anew discovered invention by Panagiotis Stefanides
based on π = 4 / sqrt[Φ]
Proof [ Copyright 1986 -2019]:
http://www.stefanides.gr/pdf/2012_Oct/PHOTO_12.pdf
http://www.stefanides.gr/pdf/2012_Oct/PHOTO_12.pdf
Proof that π = 4 / SQRT[Φ] :
© Copyright 1986 – 2019, Eur Ing Panagiotis Chr. Stefanides BSc(Eng)Lon(Hons) MSc(Eng)NTUA TCG CEng MIET
Thank you Panagiotis. This is a simple and elegant construction compared to most I’ve seen as proofs of this relationship. Some commentary in notes would likely help many readers to better understand it.
Dear Gary I thank you..
I attach the simplest form with description of conditions for the soilution, and further link showing the ruler and compass solution for the quadrature conditions:
1] http://www.stefanides.gr/Html/QuadCirc.html
2] http://www.stefanides.gr/Html/piquad.html
Regards,
Panagiotis Stefanides
Gary, I attach the simplest form with description of conditions for the solution, and further a link showing the ruler and compass solution for the quadrature conditions:
1] http://www.stefanides.gr/Html/QuadCirc.html
2] http://www.stefanides.gr/Html/piquad.html
Panagiotis, I thought it might interest you to know that Kepler’s Golden Triangle can be used to obtain a value of 3.144605 for pi (which is identical to the value you came up with). The Indian mathematician Ramanujan devised algebraic equations that have approximated pi to several decimal places. He also discovered a formula that produces the same close estimation created here by my diagrams: (9/5 + √9/5) = 3.14164. Who knows how he came up with that?
My work of giving interpretation of Plato’s MOST BEAUTIFUL TRIANGLE , SPANS MANY MANY YEAR.THIS TRIANGLE AS STATED IN MY CONFERENCES CONTAINS THE MAGIRUS/Kepler one.
Please give me the name of anybody and its copyright date of proving of the problem,!
N.B. PROFESSOR ROGER HERZ-FISCHLER reference
https://books.google.gr/books?id=066T3YLuhA0C&pg=PA81&redir_esc=y&hl=el#v=onepage&q&f=false
KEPL;ER / MAGIRUS IS SIMILAR TO , COMPOSIT PART OF AND NOT THE SAME AS PLATO’S MOST BEAUTIFUL TRIANGLE .
REF:
http://www.stefanides.gr/Html/platostriangle.html
π = 4 / SQRT[Φ] generates a value for pi at 3.144605509. But the diagrams above generate an even tighter approximation which reflects the well-known equation: (ф² ÷ 5) = (π ÷ 6)… This gives 3.141640786 as a value for pi; which is 99.85% accurate for true pi. If you check out my website you will see that the circle can be squared with exact precision on Riemannian Manifolds of positive curvature.
circleissquared.com
CHRIOSTOPHER, THANK YOU.
RULER AND COMPASS SOLUTION IS THE REQUIREMENT BY CLASSICS:
http://www.stefanides.gr/Html/piquad.html
I send you my easy way of squaring the circle regarding to Phi with two squares, and compas to find the root of Pi / 2
http://fermancebo.com/Squaring_regarding_Phi.html
Pi value?
check with this calue circle area with a square area,
and another set cor perimeter and circumferencecheck
I send you my easy way of squaring the circle regarding to Phi with two squares, also compas to find the root of Pi / 2
http://fermancebo.com/Squaring_regarding_Phi.html
Dear Mr. Meisner,
there must be one special cone with the same special proporcions as the great pyramid with
very special features.
I think this special cone is also very interesting, but I haven´t seen it in your very exciting web page..
The base circle has a cirumference of ca. 8, the radio is ca. square root of phi is ca. 1,273239, and the hight is Phi, the angle of the slope is 51,8272°.
There must be other special interesting relationships, which I couldn`t not see til now so quickly.
I would call it the “golden Cone”.
Your sincereley
Jürgen Beck
I like your “golden cone” concept. Thanks for sharing!
There is an other interesting thing that is symbolic if you look at the ratio of the numbers 16 and 18
16 : 18 = 0.888888888888…
On the left side zero symbolically a circle with an irrational, never-ending (8) circumference.
On the right side we have an endless chain of infinities.
It seems as if the nothingness (0) is facing its opposit of everything (8).
Friends I put you web with the square of the circle approximation to six decimal places (0.000005) using the number Phi.
http://fermancebo.com/Squaring_circle_phi.html
Very nicely explained. The golden ratio is really crucial to create mathematical as well as visually balanced designs. Your steps will definitely help learn others to increase their knowledge. Keep up the good work