The application Phi gives superior results in acoustics.
It is believed the Greeks used Golden Ratio to achieve the wonderful sound and “ideal acoustics” that Golden Proportion rooms have. Many cathedrals also use the Golden Section, in part, for the same reason. The Golden Section not only minimizes acoustic resonance, it also imparts a very musical quality to the remaining sound.
Phi gives superior performance and acoustics in the design of musical instruments

Stradivari used the golden section in the design of his masterpiece violins that are sought out hundreds of years later for their exquisite tonal qualities. The Fibonacci series is directly related to western musical scales, as described on the Music page.
Jody Espina of JodyJazz.com has applied phi in the design of his premier saxophone mouthpiece, the JodyJazz DV, where DV stands for Da Vinci. Per Jody:
“Every measurement was analyzed with Phi in mind and used when applicable. This included the length of the bore, the width of the shank walls, the beak of the mcp, the depth of the bore at the facing and others. The amount of harmonics in the sound, and therefore the projection of the mouthpiece, is huge. This eliminates the annoying shrillness that is associated with loud, bright mouthpieces.”

Using phi in sound studio design
The Recording Institute Of Detroit built a “Golden Section Studio” to phi proportions. They report that:
“The result of using the Golden Section in studio construction is a remarkable “even” quality with regard to frequencies. Your voice has pretty much the same frequencies present when you talk in any part of the room, the reverb has the same frequency spectrum as the direct sound. Drummers love the way their drums sound and record in this room. There is only approximately 33% of the surface area treated for acoustical absorption making this room quite live. It is a great room to record a distant mic on a lead guitar.”
The studio design is as follows:
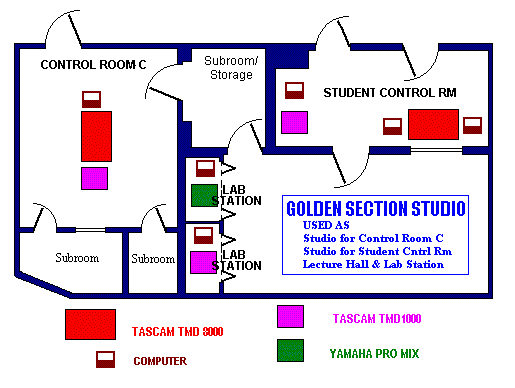 Reference and image source: Recording EQ Magazine
Reference and image source: Recording EQ Magazine
Phi gives superior acoustics in speaker wire design
Cardas Audio uses a patented design (U.S. Patent Number 4,628,151) for speaker wires that is based on the golden section. Each strand is in a phi proportion to the others.
According to Cardas:
“Alternating current can shake a wire like a guitar string. The signal’s cyclic effect causes all the wire in the system to vibrate and ring to the resonance of the alternating current. Each and every strand in a cable has its own note or beat. Two or more wires of the same mass and tension have common resonating points and share the same note.
There is only one way to eliminate the harmonic or resonant effect produced by the conductor itself. Create a multiple strand conductor, where the individual strands share no common mathematical node or resonant point and in effect absorb or cancel the noise they each create.
The infinitely indivisible progression known as the golden section is the key to resonance control. No other cable geometry, no other conductor design, can create the listening magic of Golden Section Stranding. In Golden Section Stranding, strands are arranged so that every strand is coupled to another, whose note is irrational with its own dissipating conductor resonance. This creates a silenced conductor, allowing Cardas cable to produce the purest possible audio signal. No other cable geometry, no other conductor design, can create the listening magic of Golden Section Stranding.”
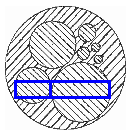
Reference and image source: Cardas Audio



It is easy enough to make the length and width of any room using the phi relationship. But what about the third dimension – the height of the room? Certainly it must make a difference acoustically, yet there is no measurement given. Is there any standing “golden cube” rule/school of thought?
I’ve been working on applying 2-dimensional logarithms into 3 dimensions. When I’m done, I’ll share my results.
No, not that I know of, really.
Hi,
I would be interested as well. I have searched the Internet for the same with no luck….
Thanks
I have not checked the details but my first guess would be
W/H=L/W=phi would be a good candidate for the three-dimensional case.
L/H=1+phi which is almost as irrational as phi.
phi=1+1/(1+1/(1+1/(1+1/(1+1/(1+1/(…
while
1+phi=2+1/(1+1/(1+1/(1+1/(1+1/(1+1/(…
IDK, but Arthur C. Clarke talked about a 2x4x9 monolith… seems there might be something in there… the dude was some kind of genius.
The 3-dimensional ratio is .618 x 1 x 1.618 so height is A, width is B, and length is A+B.
Richard Merrick suggests that a golden ratio speaker enclosure can be built in the ratios 1.62 (length) : 1 (width) : 0.62 (height).
See the article ‘Harmonic Formation’ in Token Rock (www.tokenrock.com)
Hope this helps
If I don’t know that much about music scales and I want all my music in the golden phi ratio 1.618, how do I buy more of this music?
where do I find more music to download in the Golden phi Ratio 1.618 music? thanx
Recently
Recently I discovered a property of the Fibonacci series. the sum of square of any two consecutive numbers in the series is another Fibonacci number. I found that this property agrees with the result of
first 30 numbers. Bit there is no way proving it , that it is common to other numbers too. I f is so, can we declare as a conjecture. Any one who is interested in this can you enlighten me on this.
P. Jayathilaka.
185/3, Pokunawatta ,Gangula
Pandura.
Sri Lanka.
2017 . 06. 16.
I
That is true. In fact F(2n-1)=F(n)^2+F(n-1)^2, where F(n) is the nth Fibonacci number.
F(0)=0, F(1)=1, F(2)=1, F(3)=2, …
Another relation is that F(2n)=F(n+1)^2-F(n-1)^2.
An induction proof follows:
1) For n = 2, both statements are true.
2) Assume that both statements are true for n=k, if we can prove that the statements are true for n=k+1, we are done. From the definition of the fibonacci sequence, we have
F(2k+1)=F(2k)+F(2k-1)
Now we use the assumption that the statements are true for n=k. That is
F(2k+1)=(F(k+1)^2-F(k-1)^2)+(F(k)^2+F(k-1)^2)
That is
F(2k+1)=F(k+1)^2+F(k)^2 (1)
It remains to show that F(2k+2)=F(k+3)^2-F(k+1)^2.
I leave that as an exercise.
Thank you very much.
Hi, I’m really confused about the speaker wire design. I know it stated many times that Cardas uses golden ratio or golden section in the design, but I can’t seem to see where he applies it
The golden ratio is in the diameters of the various wire sizes bundled in the wire cable. I’ve added an extra image above to show this more clearly.
Thank you. But how does the golden section affects the resonance in the wire?
The best explanation I can offer is found on the Cardas website here:
http://www.cardas.com/insights_golden_section.php
http://www.cardas.com/insights_golden_ratio.php
Note these passages in particular:
Alternating current can shake a wire like a guitar string. The audio signal in a stereo system is seen as alternating current. The audio signal, be it digital or analog, through tube or solid state, is always alternating current. The signal’s cyclic effect, causes all the wire in the system to vibrate and ring. This ring becomes a song sung to the resonance of the electrical and mechanical components of the cable. Every interconnect, every speaker cable, every chassis and speaker wire has its own song. The stored mechanical and electrical tension and time delay characteristics of the cable determine what song is sung. Each and every strand in a cable has its own note or beat. Two or more wires of the same mass and tension have common mechanical resonating points and share the same note. Two or more wires or bundles of wires, differing in size, each have their own resonant points. When combined, wires find new points of interaction, creating yet another note. The sound produced by any stereo system depends on the purity of the audio signal. When the cable that links all the components together imparts its own sound the audio signal is corrupted.
Other related articles on their site include:
http://www.cardas.com/room_setup_golden_trapagon.php
http://www.cardas.com/room_setup_golden_cuboid.php