Musical scales are related to Fibonacci numbers.
 The Fibonacci series appears in the foundation of aspects of art, beauty and life. Even music has a foundation in the series, as:
The Fibonacci series appears in the foundation of aspects of art, beauty and life. Even music has a foundation in the series, as:
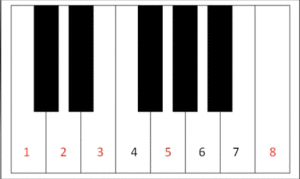
- There are 13 notes in the span of any note through its octave.
- A scale is composed of 8 notes, of which the
- 5th and 3rd notes create the basic foundation of all chords, and
- are based on a tone which are combination of 2 steps and 1 step from the root tone, that is the 1st note of the scale.

Note too how the piano keyboard scale of C to C above of 13 keys has 8 white keys and 5 black keys, split into groups of 3 and 2.While some might “note” that there are only 12 “notes” in the scale, if you don’t have a root and octave, a start and an end, you have no means of calculating the gradations in between, so this 13th note as the octave is essential to computing the frequencies of the other notes. The word “octave” comes from the Latin word for 8, referring to the eight tones of the complete musical scale, which in the key of C are C-D-E-F-G-A-B-C.
In a scale, the dominant note is the 5th note of the major scale, which is also the 8th note of all 13 notes that comprise the octave. This provides an added instance of Fibonacci numbers in key musical relationships. Interestingly, 8/13 is .61538, which approximates phi. What’s more, the typical three chord song in the key of A is made up of A, its Fibonacci & phi partner E, and D, to which A bears the same relationship as E does to A. This is analogous to the “A is to B as B is to C” basis for the golden section, or in this case “D is to A as A is to E.”
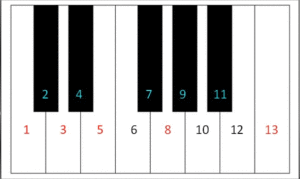
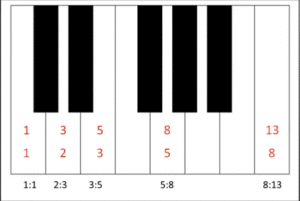
Here’s another view of the Fibonacci relationship presented by Gerben Schwab in his YouTube video. First, number the 8 notes of the octave scale. Next, number the 13 notes of the chromatic scale. The Fibonacci numbers, in red on both scales, fall on the same keys in both methods (C, D, E, G and C). This creates the Fibonacci ratios of 1:1, 2:3, 3:5, 5:8 and 8:13:
- 8 notes of the octave scale
- 13 notes of the chomatic scale
Musical frequencies are based on Fibonacci ratios
Notes in the scale of western music are based on natural harmonics that are created by ratios of frequencies. Ratios found in the first seven numbers of the Fibonacci series ( 0, 1, 1, 2, 3, 5, 8 ) are related to key frequencies of musical notes.
| Fibonacci Ratio | Calculated Frequency | Tempered Frequency | Note in Scale | Musical Relationship | When A=432 * | Octave below | Octave above |
| 1/1 | 440 | 440.00 | A | Root | 432 | 216 | 864 |
| 2/1 | 880 | 880.00 | A | Octave | 864 | 432 | 1728 |
| 2/3 | 293.33 | 293.66 | D | Fourth | 288 | 144 | 576 |
| 2/5 | 176 | 174.62 | F | Aug Fifth | 172.8 | 86.4 | 345.6 |
| 3/2 | 660 | 659.26 | E | Fifth | 648 | 324 | 1296 |
| 3/5 | 264 | 261.63 | C | Minor Third | 259.2 | 129.6 | 518.4 |
| 3/8 | 165 | 164.82 | E | Fifth | 162 (Phi) | 81 | 324 |
| 5/2 | 1,100.00 | 1,108.72 | C# | Third | 1080 | 540 | 2160 |
| 5/3 | 733.33 | 740.00 | F# | Sixth | 720 | 360 | 1440 |
| 5/8 | 275 | 277.18 | C# | Third | 270 | 135 | 540 |
| 8/3 | 1,173.33 | 1,174.64 | D | Fourth | 1152 | 576 | 2304 |
| 8/5 | 704 | 698.46 | F | Aug. Fifth | 691.2 | 345.6 | 1382.4 |
The calculated frequency above starts with A440 and applies the Fibonacci relationships. In practice, pianos are tuned to a “tempered” frequency, a man-made adaptation devised to provide improved tonality when playing in various keys. Pluck a string on a guitar, however, and search for the harmonics by lightly touching the string without making it touch the frets and you will find pure Fibonacci relationships.
* A440 is an arbitrary standard. The American Federation of Musicians accepted the A440 as standard pitch in 1917. It was then accepted by the U.S. government its standard in 1920 and it was not until 1939 that this pitch was accepted internationally. Before recent times a variety of tunings were used. It has been suggested by James Furia and others that A432 be the standard. A432 was often used by classical composers and results in a tuning of the whole number frequencies that are connected to numbers used in the construction of a variety of ancient works and sacred sites, such as the Great Pyramid of Egypt. The controversy over tuning still rages, with proponents of A432 or C256 as being more natural tunings than the current standard.
Musical compositions often reflect Fibonacci numbers and phi
Fibonacci and phi relationships are often found in the timing of musical compositions. As an example, the climax of songs is often found at roughly the phi point (61.8%) of the song, as opposed to the middle or end of the song. In a 32 bar song, this would occur in the 20th bar.
Musical instrument design is often based on phi, the golden ratio

Fibonacci and phi are used in the design of violins and even in the design of high quality speaker wire.
Insight on Fibonacci relationship to dominant 5th in major scale contributed by Sheila Yurick.
Do you know of other examples of the golden ratio in music? Submit them below.



The whole overtone series is a series of golden ratios. If you divide an octave by a perfect fifth, (13/20), you get the golden ratio. If you divide a perfect fifth by an octave, (8/13), you get the golden ratio. If you divide a perfect fourth by a major sixth, (6/10), you get the golden ratio. And if you divide a major third by a perfect fifth, (5/8), you get the golden ratio. The overtone series is a natural order of notes that is played by horn instruments and found in other instances in music.
I’m sorry but I don’t understand. I’ve done research and it says that the golden ratio 1.61803… and so on, but 13/20 = 0.65, 8/13 = 0.615… , 6/10 = 0.6, and 5/8 = 0.625. Sorry for not understanding, could you please elaborate?
One of the properties of Phi, 1.618, is that its reciprocal is 1 less than itself, or 0.618. You can either compare the numbers you listed to 0.618 or just flip the numerator and denominator to get 21/13 = 1.615, 13/8 = 1.625, 10/6 = 1.666 and 8/5 = 1.6000. Note that you should use 21 though, not 20. You can use 1.618 and 0.618 interchangeably by doing multiplication or division.
Becky, the question you’re having regards the convergents of two consecutive terms in the Fibonacci sequence. The further along in the sequence, the closer the ratio approaches the value of Phi.
1, 1, 2, 3, 5, 8, 13, 21, 34, 55, ….
1/1,
2/1,
3/2,
5/3,
8/5,
13/8,
21/13
etc…
these approach the golden ratio, Phi.
can i know more about how the Fibonacci helps in the invention of the violin
I don’t know that it had a role in the invention of the violin. Apparently master violin makers found that it played a role in improving it.
phi is the most non resonant ratio (the best way to mute specific freqs. So if you uphold this in the design all tones are somewhat equal in volume. It is the opposite of harmonic ratios basically.
“P”hi with and uppercase “P” is 1.618 but when it is lowercase, it is .618
Becky,
The golden ratio is (1 + sqrt(5) / 2). If you have a spreadsheet pick any column – let’s say for example D. Make D1 = 1. Make D2 = 1. Make D3 = =D1+D2. Then put your mouse on the lower right hand corner of D3 and drag it down the D column to D1400. Now go to another column and enter (D1400 / D1399). Then widen the column. A few cells below that enter ((1 + sqrt(5))) / 2. Make sure to enter it precisely like this with the parentheses as I placed them. Press . What you see should answer your question.
Bravo for giving the golden ratio exactly (1+sqrt(5))/2, rather than giving a decimal approximation. This draws a good distinction between the pure mathematics and its applications. I think most people have some tacit feeling that ‘if it’s not expressed as a decimal, then it’s not realy a number’. Even as a person with a physics degree, I remember being slightly uncomfortable when I first typed Sqrt[2] as Mathematica input and got ‘radical 2’ as the output 🙂
man thanks so much , i am doing a maths project and that answer goes perfect with my question. I straight away copied and pasted it
Well… if you’re using the overtone series as your natural guidepost, which I fully advocate, it doesn’t make much sense to then switch to equally tempered half-steps. Those half-steps aren’t really a direct result of the overtone series, they result from the 12th-root of 2 (2^(1/12)), the 2 representing the octave overtone and the 12 being the number of half-steps needed to fit in one octave… so the equally tempered half-steps you’re treating as similarly natural to the overtone series are actually produced by an equation designed by humans. I suspect you may be onto something with the relationship of phi to ratios within the harmonic series, but a proof of such a phenomenon would require much more than you’ve provided. Also, the perfect fourth and major sixth (12th overtone isn’t quite major) don’t appear naturally in the overtone series — at least, not until the partials are very close. If you could explain the existence of the Pythagorean comma by way of phi, then you’d really have something going.
And in his Theory of Harmony, Schoenberg gives a much simpler explanation of the phenomenon of the I, IV, and V chords based on the overtone series, with no “approximations” required.
For Kenny (If you could explain the existence of the Pythagorean comma by way of phi, then you’d really have something going.) http://www.gci.org.uk/images/s&mbsecret.png
a perfect fifth is 3/2 ……… if you divide an octave (2/1) by 1.5 you get 1/3 .. if you times an octave by a perfect fifth you can keep doing it again and again and you will never get back to the octave.. similar to how phi doesn’t have an end.
Interesting they pointed out this applies to western-style music, where the smallest increment in a mode is a helf-step. I’m going to have to research how it applies to eastern-style modes and scales where the smallest increment is a quarter-step.
the number “Phi” is an unreachable, approximation; which in this case functions much like the number “infinity”. They are both “asymptotes”; so changing the approach to 1/4 tones won’t change the unreachable-limit. Also consider how notes and scales are derived from a whole, and are thus parts of that whole; rather than being wholes, themselves, that are cleaved together into an amalgamated composition–that is if notes were wholes then they would be called scales.
Fascinating! I’m wondering how Fibonnaci applies to the sort of chord sequences that I love working with which are based on jazz and bossa nova. I wonder if rhythms work within the same principle but based on the human heart beat?
I came across a brief abstract about wave formation of the drum head. It’s a symmetrical formation but maybe there’s some Fibonacci that accounts for the wave carrying itself out into the atmosphere?
Also, if you continue the series, you arrive at 55, which is of course a lower octave of A=440hz. If you multiply 13, the 7th number of the fibonacci sequence, in order to find its octaves, you arrive at 416hz, which is approximately 1/2 step below 440hz, with an error of +.70hz.
In agreement with Becky and perplexed by Gary’s reply, I suggest a simple equation; 440 Hz multiplied by 1.618 is 711.92 Hz. This is not a tone in the western diatonic based on A=440 Hz. The frequency 711.92 Hz lies between F4 and F#4.
@Gary, how is it that 21/13 = 1.615, 13/8 = 1.625, 10/6 = 1.666 and 8/5 = 1.6000 have anything to do with 1.618 ?
I did some research in microtonal relationships for a job a couple years ago and found that Phi does not lead to anything the western ear recognizes in either harmony or rhythm. It does have some basis in eastern and northern African music though.
2, 3, 5, 8 and 13 and 21 are numbers in the Fibonacci sequence. The relationship to Phi is that that ratio of each one to the one before it converges on Phi as you go further in the sequence. See the Fibonacci Series page for more information. You’re correct that in music the fundamental relationships between notes in Western scales are much more closely related to the numbers of the Fibonacci series rather than Phi itself. The simplest harmonics, such as those heard when plucking a guitar string, are based on the string being divided into 2, 3, 4, 5 or more sections. Western music sales use a scale of 8 tones, while oriental scales use 5 tones.
Hi Robert,
I’d be interested to hear more about your research, particularly anything pertaining to the significance of the golden section in north African music.
Best,
Alex
Yes Robert, your research sounds very interesting. I would like to know more about phi in eastern and african music!
Hi so I’m not great musician but I do love math and music. I find myself somewhat confused though on part of your first defense of the Fibonacci sequence in music. The part I speak of is “5th and 3rd notes create the basic foundation of all chords, and are based on whole tone which is 2 steps from the root tone, that is the 1st note of the scale.” I was wondering if you could explain this in simpler terms for me as I find this quite fascinating.
Take a C chord as an example. It consists of the C, E and G notes. E and G are the 3rd and 5th notes of the C scale. E is 2 whole tones from C. The 13 note scale breaks down into key notes defined by 8, 5, 3, 2 and 1, as does the Fibonacci series.
Already mentioned a bit in the comments above though not totally, but the golden ratio follows automatically if you make a scale of harmonic positions on a string like is done in the bottom of this picture. http://www.zotzinguitarlessons.com/wp-content/uploads/2012/03/A4.png
Then you follow the rule of finding every most simple fraction between the two last found ones.
The simplest fraction between 0 and the open string is the octave (1/2).
The simplest fraction between 1 and 1/2 is 2/3.
The simplest fraction between 1/2 and 2/3 is 3/5.
etc.
This proces approximates phi and is the best damping position on the string. So phi is the exact opposite of a nodal position on a string. It’s the limit of the harmonic series function. Since it’s perfect for damping it’s logical it’s being used in instrument building as well as speakers, because then you are sure the object is not resonating on specific tones. You want the object to react identical in any frequency it produces.
This picture shows the proces, but doesn’t mention the rule of finding the most simple fraction inbetween the previous two.
What Phi (the golden ratio) Sounds Like6/15/2012
To buy a high quality mp3 of this song: http://www.cdbaby.com/cd/michaeljohnblake Phi = φ = 1.61803398874989484820458683436563811772… “What Phi (the golden ratio …
Per the composer: “What Phi (the golden ratio) Sounds Like” is a musical interpretation of the mathematical constant Phi. The formula I use to translate the digits of Phi into music is as follows: 1=C, 2=D , 3=E , 4=F , 5=G, 6=A, 7=B, 8=C octave, 9=D octave, 0=no note is played. The melodies that you hear throughout this piece are taken directly from the first 39 digits of Phi. The tempo is set at 161.8 BPM.” A very creative, and well executed, interpretation. It would be interesting to create and hear other interpretations of phi in which the frequencies of the notes themselves are based on golden ratio proportions.
That would be cool! Also, What about flats and sharps in the translation?
Flats and sharps are just half steps down or up between whole tones, so they could still be half of the way between whole tones in a golden ratio scale or … perhaps there should be two dividing points between whole tones, one at 38.2% and one at 61.8%, using 1/phi and 1/phi squared.
I have a question, if you wanted to express a Pythagorean 3,4,5 triangle musically what 3 keys would you need to strike to get the same relationship?
I’m not a musician, but I would guess either: C-E-F#, or C-E-A#. Look up harmonisphere, it’s what got me interested in music.
Pyth Triangle (3,4,5) ….A minor?…..A, (Bb, B,) C, (Db, D, Eb) E, (F, Gb, G, Ab) A….?
Major triad is 3,4,5 too. inverted as 4,3,5
Consider A,C and E the vertices and don’t count A twice.
A Pyth Triangle (3,4,5) represents the third, fourth and fifth overtone over the fundamental. So if we were in the key of C major, this would give G (3:2), C(4:1) and E (5:3) which is a second inversion of the chord C major.
E is (5:4) 🙂
Great thread and I love the composition what phi sounds like. I recently submitted a shot piece of music to video for my degree. There is heavy use of the Fibonacci series throughout this piece. It may be late to the party but here it is
https://youtu.be/pVDBAF_3PdM
The problem with this is you could use Pi or any other non repeating decimal and it would sound essentially the same (just the notes of C major in various orders). It’s maybe a creative way to write some music and it’s a nice little video but it is no way to get some deep musical impression of what phi “sounds like”. Sorry if that makes me a hater. Ha.
I find it beautiful the similarities between this and the most significant piece of music I have ever heard in my life:
Thanks Gary!
I don’t know a lot about music…but I heard an interesting conversation earlier this week that came to mind when I saw this site a few minutes ago. Does a Fibonacci sequence have anything to do with the so-called “Devil’s Interval or “Flatted Fifth” chord?
The flatted fifth doesn’t seem to be related to the Fibonacci series or phi. A flatted fifth is six half tones up from the root, with six more half tones up to the octave. The ratio of its frequency to the root is the square root of two, and the ratio of the octave to the flatted fifth is also the square root of two. As an example, starting at A440, the flatted fifth E flat, has a frequency of 622.254, which is 440 times root two (1.414214), with the octave at 880.
Seems to makes sense, Gary, since phi is inherently linked to what we believe is “beautiful,” and the tritone has historically not fit that description.
The “devils note” does occur in the harmonic series as the 10th harmonic. The note occurs in ancient music but was removed because of its dissonant sound…this was the beginning of western music moving away from the sound of the natural occuring harmonic series.
Thats great Gary really good information regarding equal temp and overtone series, it would be quite something to link it with the pythagoras comma. I have been using math and playing with ideas re composition for some time. Interesting idea to experiment with Phi and frequencies etc. I will have a listen to that piece soon.
@ Darren, might not be quite what you are after, here’s some ideas,you could try calculating the frequencies of notes and squaring them and then try to find 3 frequencies that match the Pythagorean triangle, or find another series of pythagorean triplets as they are known eg 5^2+12^2=13^2 or a larger one 99^2+4900^2=4901^2. I’d be surprised if any of them matched the equal temp tuning.
Or in the overtone series, the 3rd harmonic is G, 4th is C and 5th is E, so a C chord or squared , 9+16=25. The 9th overtone is D, 16th is C and the 25 th is a G of sorts -27 cents.
I’d be interested to see if anyone else has some ideas in this regard.
Phi occurs in the Pythagorean comma when you take the ratio in cents between the pythagorean circle of fifths and the tempererd circly of 5ths.
This ugly image shows the values in the colored boxes.
http://www.gci.org.uk/images/s&mbsecret.png
You take the first number out of the purple row and divide this through the second. Then the results are the green numbers. Green approaches phi.
Hey Gary. This may be off topic, but I was wondering if you could apply colors to the phi ratio and to the corresponding notes in the scale? Also, if there was a 3d representation of these sounds or of the phi ratio itself? Thanks so much.
You can apply the golden ratio / phi to colors. Musical scales though are based on octaves, with each octave being based on a doubling of the frequency, and with each note in a 12 tone scale being a increase of the 12th root of 2 from the one before it. That fact would probably override the exact application of the golden ratio. Anyone else have any creative thoughts?
C-UTerus 16 32 64 128 256
C# 17 34 68 136 272
D- REign/region 18 36 72 144 288
D# 19 38 76 152 304
E-MIxtus orbis 20.25 40.5 81 162 324
F -FAtum 21.5 43 86 172 344
F# 22.75 45.5 91 182 364
G-SOL/ar 24 48 96 192 384
G# 25.5 51 102 204 408
A-LActeus 27 54 108 216 432
A# 28.5 57 114 228 456
B-SIdereus orbis 30.5 61 122 244 488
I found it interesting when i saw video of 440vs432 and on the “SOL” note you could see the sun(or multiple suns) (Cymatics experiment 432-440Hz by Holonmusic432Hz)
So the “sol” frequencies are like the 24 hour cycle(cycles per second=hertz)
60secondsX60minutesX24Hours a day=86400 (this is A=432X2) and so on.
When i imput all the frequency in Excel i started subtracting the C# with C, D with C# and so on and i found this numbers that occur in Cycle computing For exsample 0.75 wiuld be 3/4 of a circle 1 =full circle 1.25=Circle and 1/4, 1.5=Circle and half..so on and so on.
0.75 1.5 3 6 12 24 48 96 192 384 768
1 2 4 8 16 32 64 128 256 512 1024
1.25 2.5 5 10 20 40 80 160 320 640 1280
1.5 3 6 12 24 48 96 192 384 768 1536
2 4 8 16 32 64 128 256 512 1024 2048
I find this much interesting. Computer RAM progression(geometric) and progresions for Screen resolutions (16:10 Phibonacci,its should be 16,2:10 roughly )
13 is a magic number (star of david=male and female principle in the male,and another male and female in the female together they are 12 sided star of david and the point of manifestation is the new octave,”Do” dominion Point zero ,perfect state)
Much to be said here but then again Im still learning. thank you for the post.
I liked this book in some of my research on this interesting and extensive topic:
http://www.planetware.de/octave/index.html
I’m new to the math here – day old in fact! I just ordered a custom metal torus shape tongue drum – it’s got 9 tongues. I asked for it to be tuned to 432 hz with the golden mean / Fibonacci sequence – and with 9 tongues and the 432 this could also well connect with the 9 major chakras (still figuring it out before the smith finalizes the tuning).
I quickly learnt that’s not straight forward. With their great help as well as a web search – this was my favored landing place as I realized quickly Gary and co are right on the money here – and with help from Gary’s musical chart above as well as Darwe’s input I came up with a ‘formula’ for this – below is sort of an inverse math check (I’m not fully sure of how accurate this is and also realize Fibonacci and octaves need assistance to combine):
Relating the 9 notes mathematically to 432 hz:
C256 x 1.5 x 1.5 x 1.5 div 2 = 432
D288 x 1.5 = 432
E324 x 2 div 1.5 = 432
G384 x 1.5 x 1.5 div 2 = 432
A432 x 1 = 432
C512 x 1.5 x 1.5 x 1.5 div 2 div 2 = 432
D576 x 1.5 div 2 = 432
E648 div 1.5 = 432
G768 x 1.5 x 1.5 div 2 div 2 = 432
How does this look – does this work?
Thanks, Jeremy
I haven’t had time to study the above page that you mentioned, but have been looking at the relationship of colors to musical tones.
What I’ve found, is that C 41 octaves above middle C is probably 563 THz, equated by doubling 256 41 times, or 256X2e41. Rainbow color C is 566 THz, the range of Green being 540-610 THz.
The other notes and colors are:
D (288Hz) is 633Thz 41 octaves higher, equalling Rainbow Blue (638THz, blue ranging from 610-670THz)
E (324 Hz) is 712 THz 41 octaves higher, equalling Rainbow Violet (714THz, violet ranging 670-750THz)
F is 756THz, just above violet, G is 422 THz 40 octaves above middle C, rainbow red being 428THz, the range given for red 430-480 THz.
A (432) is 474 THz 40 octaves higher, so on the very orange side of the red scale, B(486) is 534 THz 40 octaves higher, with is within the yellow range (510-540THz). I have more to add but need to do something else now.
Hello,
I´m writing my term paper for school about this topic, Does anyone know the author of this great article? =D
I´ll be very thankful about an answer because I need the name for a citation.
Hi Carola. I’m the author of the entire site. Information on references can be found at https://www.goldennumber.net/content-images-use/. Thanks for your interest. Gary Meisner
Hi Gary Meisner,
thank you very much for your answer! It´s very helpful for me!
Your article is very interesting! I hope it´s ok for you, if I citate a sentence of your text.
Carola
References to the site are always appreciated.
Hi. Thanks for your article. I came across it while doing generic research further applying Fibonacci to my day trading. I never before realized there are 13 notes in an entire octave. I’m often amazed at how this series is involved in so much around us.
hi gary. thanks for the info.
looking for 1 note that represent the phi. what note should it be ?
you can suggest several notes ofcourse.
thanks
shai
If I had to pick just one note, I suppose it would be the one with a frequency of 161.8 or 1618 cycles per second. The golden ratio though is about a ratio of two things though, so that would mean it would be better to pick a note and the one that is 1.618 or 0.618 times its frequency.
hi , i have brain damage , so i keep it simple on 5ths and golden mean proportion ( which ratio stays the same despite the size used ) and for me its the model of perfect compresssion in nature ,..
if starting at D 144 hz ( 432 @ 216 attune ) if starting at 144 to go up a golden ratio i would multiply it by 3 and divide it by 2 , like pythagoras did ,, all the heady music maths make me swoon ,, so :
144 going up the scale is 144 x 3 then divides by 2 = 216 its perfect pythagoran fifth .. and very close to perfect phi golden mean compression tones .
to go down just divide by 3 and multiply by 2 :
144 / 3 x 2 = 96 G ( i also like 144 as its in fibonachi directly )
so going up from D144 its A 216 , and down its g 96 ..
g 96 to D 144 is perfect golden mean proportions ,, the music buffs seem to way over complicate simple fifths and pythagoran fifths both ..
i see it as a shape of phases meeting a bit like a hurricane and implosion ..
The song lateralus by Tool is a good example of Phi in music.
Yessss
I need some more vivid explanation of the relationship of music with Phi, if you can give me some more. Like, how is Phi found in the musical notes, or chords or other things relating to music.
This is way too simplistic a reading of the way musical theory works and is basically a numerological approach of having a theory and trying to find facts to fit it.
We *know* how the musical scale works: An octave is a doubling of frequency per octave and then whole tone ratios (not the golden series either) give the harmonic series, which in one octave span looks like this:
C-D 9:8
C-E 5:4
C-F 4:3
C-G 3:2
C-A 5:3
C-B 15:8
C-C 2:1
And since the 1600s we’ve found that 12^2 is the best way to approximate the above and have usuable semi-tones and scales in each key.
The golden ratio struggles to explain any of this simple mathematics and adds little if nothing to our understanding of harmony.
The article does not say that musical scales are based on the golden ratio. It says they are related to the Fibonacci numbers found in nature. As you noted, tempered musical scales are an APPROXIMATION to produce the same result in any key. (That mathematical relationship, by the way, is based on 2 ^ (1/12), not 12^2.) The ACTUAL tonal relationships that you would find if you plucked a string at various harmonic points are based on the integers, just as you listed. Frequency relationships created by ratios of Fibonacci numbers do in fact produce the true harmonic frequencies of the notes in the scale, as illustrated by the chart above.
I don’t get where some of the numbers are coming from when you start putting them in ratios. But what I do find interesting is that when you go to the 432 scale, all the note frequencies are all divisible by nine. That just seems right to me. Nine is an awesome number in its properties, so it’s gotta mean something that all those 432 numbers are nines, right?
The reason the frequencies or ratio calculations don’t line up exactly (but are close) is what is called the Pythagorean comma. The Pythagorean comma is a factor that is used to multiply fundamentals (root frequencies) by to get enharmomics to sound “in tune” when using the circle of 5ths. If you google or youtube “pythagorean comma” you’ll be able to easily see the reason for its existence.
The diatonic scale can be generated using successive phi numerals squared, as follows;-
(start with 16^2 = 256)
16.618^2 = 276.16
17.618^2 = 310.39
18.618^2 = 346.63
19.618^2 = 385
20.618^2 = 425.1
21.618^2 = 467.33
22.618^2 = 512
You can check the above scale values against the 12th root of 2 values.
I don’t know why it does this though…
Lucien
I bought an allen organ old one made 1970 or so. I am playing different pieces from Bach well tempered clavichord. I also have a Wurlitzer baby grand made in China or out of USA, just got it tuned. The Bach sounded horrible.
I thought to myself, I bet Bach has a different sense of turning. I started by looking up what the differences between “well tempered” and modern tuning.
I decided to get the tuner to tune my piano exactly to the principle 8 on the
bottom keyboard. BINGO The bach sounds great on my piano. Hope the organ
is tuned to the well tempered scale.
I built a very complex series of pyramids interfacing one another. They were
all constructed golden section wise as great pyramid. It emitted such a force field
that I was almost floating. I started psychic channeling and it wrote a book.
which I called Open Door Prayer. Anyhow my life has since evolved around the golden section including enjoying playing the organ and the Bach etc
Not sure if it counts because I didn’t do the math. Resonator pipes for marimbas, and other air columns, seem to fit along a section of the Golden Spiral. It sure is neat to the see the Fibonacci sequence popup all over the Universe.
Good Day
Hi,
A previous comment mentioned A440 X I.6I8 ends up between F natural and F#.
What pitch would A432 x I.6I8 give?? Would it be F natural?
Very interesting site. Thanks.Gary.
.
lolololololololololol. I’m an avid musician myself, and very fond of the golden ratio, so thanks!
I highly recommend the work of Richard Merrick. Interference is a great read. http://www.interferencetheory.com/HarmonicTheory/Interference/Excerpts.html
I totally agree. Richard Merrick’s work on harmonics and phi is an astounding achievement, bringing together music, biology, cosmology, and philosophy and revealing their common thread through the science of harmonics.
anybody analyzed chapels ratios in other galaxies? would have been very interesting as well
Great article and website, Gary, kept me up all night, then I got to the comments. I just HAD to put my two cents, or maybe eight cents, and a fiddler’s farthing. First of all, that first comment by Ryan. Those numbers represent notes in a scale, or the 12 tones plus the octave. An interval is the relation of one tone to another. To try to divide a third by an octave makes no sense, that’s not how you find the harmonic series. It finds itself, when you shorten a wavelength, a column of air, a string, a bell or a sphere that is vibrating. You will find the beginning of the fibonacci sequence, mixed up with simpler ratios.
With the violin my main instrument, I became aware of the “pythagorean” vs. tempered problem early on, with the famous comma. The best explanation I have found is in a book called “Northern Indian Music” by Alain Daniélou. The secret? A perfect fifth and a perfect fourth should equal an octave. Ever wonder why we don’t call an octave “perfect”? Because it’s not! There is no “interpretation” of a 5th or a 4th, as there is with 3rds and 6ths. The perfect 5th and 4th added together equals 61/60ths of an octave. Thus the famous comma = 1/61st of an octave. There are 61 intervals, measured against a drone (the first note of the scale) to chose from, and each one has a specific meaning known to every North Indian, a colour, an emotion, degree of good or evil. I no longer have the book, it was a stolen university copy that a musician gave me, so I thought that I should pass it on. Some of these notes are never chosen, because of the uneasiness and negative energy they invoke, to construct the 5 to 7 note Ragas. Piano tuning, becoming a lost art with our electronic tuners, is about detuning the intervals from their simple ratios, by counting the interference beats of the “resultant tone”, which is simply the substraction of the lower tone from the higher. The closer the 2 notes, the lower the resultant tone. Gotta squish those notes into the octave, which of course is the first harmonic and the start of the fibonacci sequence.
And just briefly……. The augmented 4th, diminished 5th, the tri-tone, the devil’s interval. You missed the most obvious definition, you split an octave right down the middle, no messing about with perfect anythings. It could be THE most important interval in western music, Bach, Beethoven, jazz, rock, you name it. It’s the interval between the major 3rd and the flatted 7th of a dominant 7th chord. Everybody in the Western Hemisphere anticipates the 3rd moving up a half-step to the tonic, while the 7th just has to fall a half-step to the third, or maybe suspending your gratification and make the girls squirm a bit……………..
thanks or the book rec!
I think, instead of saying that the golden ratio is 1.618 etc, you should say that it is (1+Sqrt[5])/2, because 1.618 is just another approximation – like the others cited previously. This point is driven home by advanced mathematical software, because entering, for example, Sqrt[2] as input will produce, not a decimal number, but radical 2 as output.
See sphinx-muse.com
username: mathmuse
password: One2Free
There are a number of places on the site that show (1+Sqrt[5])/2 as a way to calculate the golden ratio. It’s most commonly expressed as 1.618, and with the understanding that four or five significant digits is accurate enough for most practical uses, be it phi, pi or other numbers.
How can that be a full scale, from the starting A to the ending A, when there are only 12 notes? Which one is missing, and why is it missing?
Thanks.
Nothing is missing. This is just a matter of semantics. There are 12 notes in the Western scale. If you count all the notes STARTING with any note and INCLUDING its octave there are then 13.
I agree that trying to force our 12 tones into a Fibonacci sequence is a bit much. What I’d really like to remind everyone is that this ratio is defined as (a+b) / a = a/b, which when solved with the quadratic formula equals ( 1 + sqrt(5) ) / 2, or 1.618 033 988 749 894 848…. or almost exactly 1.618 034 for all practical purposes. This number has the property of being its inverse minus 1, among other things, but there doesn’t seem to be any relationship to the 12th root of 2 as in the modern musical scale.
This conflates several concepts.
Pure tonal relationships can be found by plucking a string at 1/2, 1/3, 1/4, 1/5, etc. of its length. This produces pure musical harmonics and tones.
The 12th root of 2 is a mathematical accommodation used in Western tuning to create equal increments in the frequency of every note. This allows music to be played in any key and retain the same tonal relationships. The resulting frequencies are slightly different than the pure tonal relationships.
The ratio of numbers in the Fibonacci sequence do converge 1.618 as they increase, but that again is a separate concept from the relationship of the individual Fibonacci numbers to musical notes.
The most basic musical tones are related to Fibonacci numbers, as illustrated in this article. That does not mean that they’re related to Phi, or that Phi need be related to the 12 root of 2.
I was wondering if there are any examples of the golden ratio in modern pop music.
The guitar solos or other remarkable moments often occur at ± 0.618 of the lenght of songs. Verse – chorus – verse – chorus – Fibonaccimoment – chorus – verse.
Smells Like Teen Spirit has the solo there, like many other songs. Iggy Pop screams at that moment in China Girl, etc..
If you want to see fibbonacci in music listen to lateralus by Tool
http://www.youtube.com/watch?v=EDlC7oG_2W4
greetings! very interesting read, but as another commenter stated, in your chart there only twelve notes (A, A, D, F, E, C, E, C sharp, F sharp, C sharp, D, F). would also like to know what is the thirteenth note.
peace…….
The “13th” note in the illustration is simply the octave of the first note. That is a perhaps semantics or an accommodation to the perspective presented, but no scale sounds complete without the octave.
sorry this picture. http://www.tokenrock.com/stock/harmonics_PhiRec.jpg
The most obvious thing about the fibonacci numbers, as well as pi and phi goes unmentioned, instead all kinds of happenstance arbitrary associations are presented.. If one carries out the fibomacci process on any two numbers within just a few moves one begins with each further move to map out an infinite series of ratios for minor 6ths of every possible tuning, pi is a minor 6th plus an octave and phi is also a minor 6th (of course we could think of it as an aug 5th which might be more pertinent) Where does the minor sixth most often appear in musical harmony? In the final cadences where it helps to fully resolves harmonic progressions to end a piece or at least to end a portion of a piece.. Pi is also useful for this purpose giving a sense of full closure. The obvious is often the most obscure simply because it is obvious, when one expects secrets one misses what is in plain sight. This role of the minor 6th and minor 6th plus octave (pi) in attaining full harmonic closure does seem significant in that many natural designs also seem to resolve on these intervals
There are 12 notes in an octave register; 13 in an octave. The octave note begins the next octave register. An octave register based on C3 runs C3 to B3; its octave from C3 to C4.
Thank you for that distinction. Similarly, the word “octave” is derived from the Latin word for eight. The octave includes the required eighth note to complete the scale. Add in the five half tones and it completes on the 13th note.
The Pythagorean Comma feeds back to Phi http://www.gci.org.uk/images/s&mbsecret.png
The confirmation link in the email sent doesn’t work?
On the subject of musical scales, please see my ‘squared’ circle of fifths at my web site. It’s a card. Thanks.
I’ve been playing piano for 34 years and drums/percussion for 31 years and it was only a few years ago that I heard about the Golden ratio and the Fibonacci sequence. I think it’s fascinating to say the least. I ended up here while looking for information about the Golden ratio and how it applies to music. I’m currently reading a book called, “This Is Your Brain On Music: The Science of a Human Obsession” by Daniel J. Levitin. I just wanted to say that all of the comments in this thread have helped me to understand these concepts a little better.
My study and learning will continue.
I’m a musician and what I find missing from the discussion are examples of great musical works that reflect the ratio as well as those that don’t.
Thanks!
My interest in Olivier Messiaen’s Catalogue and your post led me to google: ‘golden ratio’ Messiaen and the top link was:
http://www.sinfinimusic.com/uk/watch/animations/other-animations/animation-messiaen-quartet-for-the-end-of-time-1941-2016
Hi Gary,
Curious to know if you have heard of David Sereda and his theory that there is a ancient lost music scale that is related in some way to the great pyramid’s slope angle of 51.51 degrees and of course includes Phi. He puts middle C at 515.1 Hertz? It’s a lot more detailed than that but I can’t remember the theory. Also, if anyone else has heard of his theory please let us know.
No, I’ve not heard of that. Interesting concept, but did the ancient Egyptians have trigonometry based on 360 degrees and the ability to measure sound frequencies in vibrations per second? Seems that both would be required.
Please all, make sure to also take note, as I wound up here during an investigation of the Number 9 Code, that EVERY single octave, when A=432 (9) equates to 9! From 1382.4 (1+3+8+2+4=18, 1+8=9) on back down to 162=9 (Phi) and to the lowest octave 81 (1+8=9). . . very interesting indeed. A secret to sound perhaps? The “sound” that moves the lattices in all matter? Just exploring. . .
Golden ratio is a Fact. A Octave numbers of Hertz is suggestion.
0,618 is golden ratio of 1,0 . 618 Hertzes is golden ratio of 1kHz! You should change base tone A for find PI, Alpha, your date of birth and Atlantis!
But is standard signal tone for machine… not for music. The resonanse Best A tone should be in octave os Schumann’s Earth resonance! FOr example golden ratio of 434 Hz standard tone A is 434 * 2 /( 1 + SQRT(5)) [Hz] = ~ 268.23 Hz it’s C Tone
the orbital resonance of Venus and earth is 13:8. how the hell is that coincidence?
Is this web graph depicting PHI a coincidence!
Refers to the above:- http://cc12488160114.sharepoint.com/Pages/TheBook.aspx
Thank you for this awesome article, but i am an artist and find visual information much easier to understand than numerals and theoretic formulas which totally confuse me.
Can any one explain the fibonacci in music relationships, in a visual diagramatic or illustrated way?
Thank you in anticipation.
hello, i now nothing at all, about music.
I have the following question:
what means this: C Major-7th (292hz-330hz-392hz)
C Major-7th is a chord that includes the notes C, E, G and B. In this, C, E and G are the basic chord formed from the root, third and fifth notes of the scale. The “Major-7th” is the addition of the B, which is the 7th note in a C major scale. The Hertz (Hz) references are less clear. 392hz is the G note, in a scale when A is the standard tuning of 440hz. The closest notes to the other frequencies are D at 293.66hz and E at 329.63hz. These are very close to the values you listed of 292hz and 330hz, so it may be that they are just being rounded to whole numbers. While E and G are part of the C Major-7th chord, D is not.
well, thank you so far, the meaning for my question is that i have to make binaural tones of this.
The explanation was: make 10 to 15 minutes: C major-7th (292hz-330hz-392hz-466hz), so i guess i have to now what frequency(s) that C Major -7th is.
Maybe thats just it, making binaural tones with this 4 frequency’s.
second for following pieces: What is: G Major, and… what is: D Minor.
I’ve studied voice for several years. I don’t see how you get every number correlating to the number sequence of Fibonacci, nor the Golden Ratio. You guys don’t even tell how you get the frequencies through actual Math. How do you? Prove it to me?
Have you ever plucked a guitar string to get a harmonic? When you do you’re dividing the string in integer ratios like 1/2, 1/4, etc. See this article:
When a piano is tuned, this simple approach doesn’t work because. For example, G calculated as the 5th of C is a different frequency than G calculated as a major 3rd of E flat.
So to get around this problem the standard scale was created using an “equal temperament”, in which the ratio of the frequencies of every note in the scale are equal. This is done by taking the 12th root of 2, which represents the 12 steps from one note to its octave, which has twice the frequency. See this article:
The ratios in the Fibonacci numbers can express the relationships of a number of frequencies in the scale. Not all, but some as shown in the table. Does this make sense now?
Just intoned scale 16/15, 9/8 , 6/5 etc is based on harmonics. Pythagoras’ circle of 5ths almost covers most of these freq but has a gap (Ps comma). To fill this gap you divide it over all steps and you get 12tet.
Golden ratio on a string though is the most non-resonant position, the exact opposite of the harmonic series in fact. This position is between 8/5 (near fret 8) and 5/3 (near fret 9).
Speaker designers and Stradivarius use this to mute unwanted freqs in certain keys. Their ambition is to balance out the volume and resonance for every tone the same. This has nothing to do with musical scales but with avoiding freq specific resonance. The blue diagram with all the calculations and numbers is false maths, it also works with slightly other numbers and doesn’t approach phi at all if you continue calculating 13,14,15,16etc.
The concepts and charts on this page do not relate to the golden ratio. They relate entirely to ratios that can be created with the Fibonacci sequence numbers of 1, 2, 3, 5, 8 and 13. The golden ratio point of a string is never mentioned, and I agree that it has a very non-musical result. There is also no mention of any of the ratios approaching phi with respect to music. That is, however, one of the properties of the Fibonacci sequence as you progress to the higher numbers.
But 12TET is not music, it’s a math compromis that luckily approximates many of the most just intoned ratios (9/8, 6/5, 5/4, 4/3, 3/2, 8/5, 5/3) and therefore is workable as a system. It misses for instance 7/6 (diminished minor third), 7/5 (just tritonus), 7/4 (harmonic seventh) while those values pop up in many other non-western music cultures and for in stance in Blues scales as the blue tones and are just as musical as 8/5, 9/8 or 15/9, even more mathmatical harmonic than those in fact.
This whole 7 white + 5 black connected to Fibonacci is a type of search and found proof. 13 is a matter of adapting the rules till the theory fits (there are 12 keys, not 13) and what about 21, 34, 55 etc? Those don’t pop up at all in the next octaves as remarkable spots. Also not if you change to 19TET or 31TET as Huygens was researching in an attempt to find more proper chords than 12TET can generate.
Here’s a good image of other TET options. I cannot find Fibonacci in there. https://en.wikipedia.org/wiki/Equal_temperament#/media/File:Equal_Temper_w_limits.svg
The Fibonacci connection to Western scales in the grouping of keys on a piano keyboard and the tonal frequency relationships is just intended as an interesting observation, not a complete theory of music. I agree that it doesn’t extend to higher Fibonacci numbers, and that musical scales other than those used in Western music are in common use elsewhere in the world.
It think the number 8 and 13 are fake ones in the piano example. It’s 7 and 12.
I would say the 13 keys-theory as being a Fibonacci phenomenon is another example of this:
https://i.kinja-img.com/gawker-media/image/upload/s–toHwAzat–/c_fit,fl_progressive,q_80,w_320/1488471128752720964.jpg
(If you doubt the pic is wrong, in this article that pic is debunct very well:
https://www.lhup.edu/~dsimanek/pseudo/fibonacc.htm)
I agree that the image of the Fibonacci spiral over the spray of water is a forced fit. If you use my PhiMatrix software to overlay a golden rectangle you’ll find that it doesn’t fit at all. If it were a Fibonacci spiral the two inner rectangles would have to be squares, not rectangles. So yes, it’s a bad example.
On the musical scale, you can argue it, but the fact is that a piano keyboard has a scale from octave to octave of 13 notes, with 8 with notes and 5 black notes, with the black notes in groups of 2 and 3. All Fibonacci numbers. It’s just an interesting observation, not a theory of music, so I wouldn’t read more into than that.
On the article you included, I find that most skeptics just tend to dismiss things rather than to really understand the underlying claims or principles. I’ve done a number of reviews of articles by skeptics and Ph.D.’s in math in which I show their misrepresentations and misunderstandings. Here are several for your review:
https://www.goldennumber.net/golden-ratio-misconceptions-by-george-markowsky-reviewed/
https://www.goldennumber.net/fast-company-design-john-brownlee-golden-ratio/
https://www.goldennumber.net/golden-ratio-design-beauty-face-evidence-facts/
https://www.goldennumber.net/facial-beauty-new-golden-ratio/
https://www.goldennumber.net/golden-ratio-myth/
I will the read the links later, thanks for those!
Repeating the 13 + 8 doesn’t make the claim more solid. Sceptic people will always refer to 12 + 7. The only way to solve this is to find 21, 34, 55 etc.. Unfort I couldn’t trace it in the higher TET systems.
I guess that’s what makes them skeptics! To be true to their beliefs though, they should also question the validity of other skeptics, and even the validity of their own statements and beliefs! 🙂
Good inquiry, but misled.
Phi is the ideal OPPOSITE of harmony.
Plants use phi so that leaves avoid covering each other in shadows. Non-resonant.
Whereas harmony in music is the equivalent of leaves lining up to cover each other in the most shadows. Resonant.
Yuri Landman was the only one in this thread who observed it “phi is the most non resonant ratio (the best way to mute specific freqs. So if you uphold this in the design all tones are somewhat equal in volume. It is the opposite of harmonic ratios basically.”
Good thought, but not fully developed. The applications to music on this page are based on the numbers of the Fibonacci sequence, not Phi itself. Fibonacci numbers have a relationship to Phi in the convergence of the ratios of successive number to Phi as you go higher in the series. In the lower end of the series, they are just integers whose ratios correspond exactly to the same very resonant musical ratios that can be produced as harmonics by plucking the right place on a guitar string. These pure musical ratios are slightly adjusted to our standard western tunings to allow them to be used in any key.
You’re correct that dividing a 360 circle by Phi produces a non-repeating pattern in the alignment of plant leaves that allows them to avoid being in shadows. Non-resonant, as you would say.
Phi though also has the very unique mathematical characteristic of being the only point at which to divide a line so that the ratio of the whole line to the larger segment equals the ratio of the larger to the smaller. Here we see resonance, where any other number is non-resonant. This important property of Phi allows it to appear in nature in ways that create harmony and beauty, as in the human face. Those in the design arts have applied this same property to their own artistic creations for centuries to capture the natural aesthetics that we see in design in nature. Resonant, as you would say.
.
When leaves don’t match ‘resonance’ is absent, like Emperor Evil sais. I can show you several diagrams how phi/Golden Ratio (it’s the same) relates to the harmonic series, Farey Sequence. This message board unfort doesn’t allow me to add pics.
In general: Fibo-phi appears to be the holy spirit, the harmonic series God and the Flower of Life is Jezus among natural philosophers. But that’s a very simplified vision. Science/chaos theory has taken over that role since 1980 and gives a better insight the way nature (hence also music/sound) shapes itself. Harmony of the Spheres is religion/pseudo-science/proto-science. Incomplete, selective and therefore leading soon to a phenomenon called jumping to conclusions (which is a fallacy). Better read a book like for instance Chaos by James Gleick to understand patterns in nature/life, than stick to old outdated models developed before we could figure out the phenomenon of the so called ‘strange attractor’ (Lorenz &Mandelbrot).
I think we’re talking about two different things here. Chaos theory doesn’t negate the unique mathematical properties of Phi or its many appearances in geometry. There’s nothing about these properties that are “pseudo-science” or “religion,” and nothing about chaos theory that prevents the appreciation or application of the golden ratio as a very useful tool in the design arts. Chaos theory may help us to understand why every human being looks different, but understanding the mathematical proportions of our basic facial and body structures can help us to understand what makes us all clearly human and easily distinguishable from apes and other animals.
Harmony of the Spheres (of which phi is one chapter) is an incomplete proto and oversimplified of chaos theory. The earth looks flat, but is round.
Without proper understanding the harmonic series, phi, but also Cantor set, Stern-Brocot tree, Farey sequence, the strange attractor, bifurcation theory, cymatic resonance, etc. are ALL part of chaos theory you easily assume phi is ‘the truth’ in art.
It’s called jumping to conclusions.
https://en.m.wikipedia.org/wiki/Jumping_to_conclusions
Also the order is: hypothesis, do a test/research, DISCUSSION, conclusion.
Discussion is before the conclusion. The fact that there are over 100 comments AFTER the conclusion that the piano keyboard features the Fibo sequence points out the conclusion is not solid, hence made on too poor sources. It remains a belief or hypothesis, not a conclusion. That can only be reached when you can also find a proper link with 21, 34, 55, etc.
I said that before, we’re talking in spirals, perhaps in a frequency that approaches phi 😉
First, the Harmony of the Spheres is an ancient philosophical concept that regards proportions in the movements of the Sun, Moon, and planets as a form of music. This “music” is not literally audible, but reflects a harmonic, mathematical or religious concept. This article and this site makes no such claims and has nothing to do with this.
Re Phi as one chapter of “Harmony of the Spheres,” one misuse of a concept does not mean that the entire concept is invalid for all other uses. This is called a Faulty Generalization fallacy:
https://en.wikipedia.org/wiki/Faulty_generalization
Also, there is nowhere on this site that I assume Phi to be ‘the truth’ in art. If you take the time to read the content here you’ll find that I and those who use it in the design arts recognize it as a valuable tool to aesthetically pleasing composition decisions. It’s not a silver bullet or a universal truth. Your assumption and statement here would be called the Jumping to Conclusions fallacy:
https://en.m.wikipedia.org/wiki/Jumping_to_conclusions
Lastly, the point of the article is not the Fibonacci sequence defines every aspect of music theory and scales. It was just a simple, fun observation that the 13 notes that comprise an octave in the key of C on a piano keyboard are broken down into sets of 8, 5, 3 and 2 keys, which are all Fibonacci numbers, and that many of the frequencies ratios that define the notes in a scale also use Fibonacci numbers, such as 3/2, 5/3 and 8/5 and others. It was really just that simple. Asserting that a relatively small first step leads to a chain of related inferences culminating in some significant conclusion is an example of the Slippery Slope fallacy.
https://en.wikipedia.org/wiki/Slippery_slope
I want to draw the attention of people interested in music and the golden section to my son’s publication, where an analysis of the hyperbolic-type wave equation is made from the positions of the golden section to determine
the frequencies of the sound of the notes of the first octave with the interval of the root of the eighth degree of the golden ratio 1.618, and not the root of the twelfth degree of 2.
I.S. Tkachenko, M.I. Tkachenko, Wave equation: Fibonacci functions, Luke functions and dynamic harmonic oscillatory process // “Academy of Trinitarianism”, M., El. 77-6567, publ. 23737, 16.09.2017
Хочу обратить внимание интересующихся музыкой и золотым сечением на мою с сыном публикацию, где сделан анализ волнового уравнения гиперболического типа с позиций золотого сечения для определения
частот звучания нот первой октавы с интервалом корень восьмой степени из золотой пропорции 1,618, а не корень двенадцатой степени из 2.
И.С. Ткаченко, М.И. Ткаченко, Волновое уравнение: функции Фибоначчи, функции Люка и динамический гармонический колебательный процесс // «Академия Тринитаризма», М., Эл № 77-6567, публ.23737, 16.09.2017
Gary Meisner, thank you for the link. I am curious of the impact of the phi harmonics on human consciousness as evidenced in classical forms as well as works like Gustav Holst’s The Planets and how this differs from older performances vs instruments attuned to the 440 frequency. A friend of mine described the difference between a stradivarius and any other violin as being especially crisp and clear and I have heard the difference as well. I’m writing an essay that addresses Phi and Fibonacci in a series of ritual performances called the rites of eleusis that combined poetry, music and dance, which were performed for a limited run in the early 20th century, and are reproduced by various performance companies to this day.
Freddie Mercury’s glissando climax in “Under Pressure” always gives me the chills as the near perfect phi moment in a pop song. Whether or not Bowie and Mercury were aware of the “golden ratio” or if this was only a fortunate stroke of serendipity we will perhaps never know – I like to think they knew exactly what they were doing 🙂
Hello! Sorry, but I’m a bit confused as to how the Fibonacci ratios were derived in the table of the music frequencies. Is it just random Fibonacci numbers dividing each other in some sort of pattern? I’m trying to figure that out because the Fibonacci ratios are said to be the numbers dividing the previous number; so 1/1, then 2/1, 3/2, 5/3, etc. But the table shows 1/1, 2/1, then 2/3 instead of 3/2. Could you please elaborate on this? Thank you
The number of the Fibonacci sequence that apply here are 1, 2, 3, 5, 8 and 13. The point is simply that various ratios formed from these numbers create tones of the musical scale. There is not a pattern in that per se.