Phi (Φ) was described by Johannes Kepler as one of the “two great treasures of geometry.” (The other is the Theorem of Pythagoras.)
Phi appears in many basic geometric constructions.
3 lines:
Take 3 equal lines. Lay the 2nd line against the midpoint of the 1st. Lay the 3rd line against the midpoint of the 2nd. The ratio of AG to AB is Phi, the Golden Ratio. (Contributed by Jo Niemeyer)
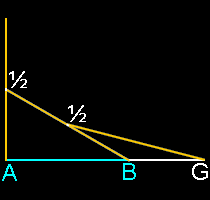
3 sides: Triangle
Insert an equilateral triangle inside a circle, add a line at the midpoint of the two sides and extend that line to the circle. The ratio of AG to AB is Phi.
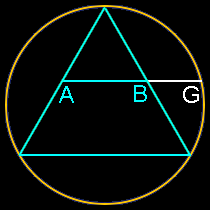
4 sides: Square
Insert a square inside a semi-circle. The ratio of AG to AB is Phi.
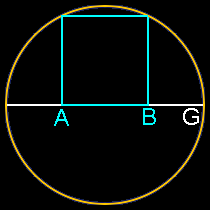
5 sides: Pentagon
Insert a pentagon inside a circle. Connect three of the five points to cut one line into three sections. The ratio of AG to AB is Phi.
When the basic phi relationships are used to create a right triangle, it forms the dimensions of the great pyramids of Egypt, with the geometry shown below creating an angle of 51.83 degrees, the cosine of which is phi, or 0.618.
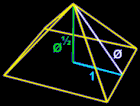
A ruler and compass can be used to construct the “golden rectangle,” as shown by the animations below, which was used by the Greeks in the Parthenon. (See also the Orthogons page.)


These same two constructions are shown in step-by-step view on Wikipedia:


Phi also defines other dimensions of a pentagon.
There are also a number of geometric constructions using a circle which produce phi relationships, as shown on the Geometric Construction of Phi in Circles page.
Phi can be related to Pi through trigonometric functions
![]()
Note: Above formulas expressed in radians, not degrees
Phi appears in 3D geometric solids
| Take three golden rectangles and assemble them at 90 degree angles to get a 3D shape with 12 corners: |
Click on the shape below and the print the page to do it yourself: |
|||||||||||||||
|
|
||||||||||||||||
This is the basis for two geometric solids |
||||||||||||||||
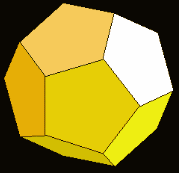
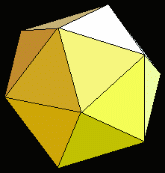
| The 12 corners become the 12 centers of each of the 12 pentagons that form the faces of a dodecahedron. | The 12 corners can also become the 12 points of each of the 20 triangles that form the faces of a icosahedron. | |||||||||||||||
Dodecahedron
|
Icosahedron
|
|||||||||||||||
|
||||||||||||||||
Some interesting aspects of dodecahedrons and icosahedrons:
A dodecahedron with sides of length 1 embeds a cube with sides of length is Phi.
An icosahedron with sides of length 1, the dual dodecahedron has sides with length 1/Phi. In other words, the dual of the dodecahedron with side of length 1 is an icosahedron with sides of length Phi.
Learn more about phi and geometry on the Penrose Tiling and Quasi-crystals pages.






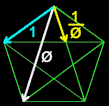
In a right triangle
c^2=a^2 + b^2
but only when a=2*b then
c=a*phi-b
and a=(c+b)/phi
examle
a=2
b=1
c=√(2^2+1^2)=√(4+1)=√5=2.23606798 or
c= 2*1.618033989-1=3.23606798-1=2.23606798
(c+b)/phi=a
(2.23606798+1)/1.618033989=3.23606798/1.618033989=2
How to show that a buckyball has co-ordinates which can be expressed terms of golden ratio?
Just see the Bucky Ball page for details and a complete list of the xyz coordinates in 3D space of all its corners and points.
I found the proof for the “3 Lines” example provided by Jo Niemeyer on another site. Jo is indeed correct, and yet again, PHI appears out of nowhere. Amazing.
Could you give me the url of the site?
and this one is a very accurate dodecahedron
http://farm9.staticflickr.com/8531/8457638482_06a7cd2fb6_k.jpg
How to construct a perfect Dodecahedron,Icosahedron and Rhombic Triacontahedron
I have nil to minimum knowledge about this but Had a dream many years ago and obsessed about what the shape was which I saw. I now know that this was it!! Thank you for that . could it be related to a piece of machinery which may be used in producing propulsion or electricity ?
Could you share some information on the machinery you are referring to? Is be very interested to know if such machinery exist and how it could be utilized for electricity
*polar star*
An interesting oberservation I made last week:
In a regular pentagon with side length=1, if you connect all the diagonals, you create a smaller pentagon within the original one, and the side length of this smaller pentagon = Phi / (1 + Phi).
This relationship also holds with regular heptagons, except in that case, there are two different diagonal lengths (I call the smaller diagonal “rho” and the larger diagonal “sigma” after this paper http://sylvester.math.nthu.edu.tw/d2/imo-training-geometry/reg-poly.pdf)
In this case, the regular heptagon has side length=1, and the smaller heptagon has side length = Sigma / (1 + Sigma).
Could this be generalized for all odd-sided regular polygons?
The inscribed pentagon example is not stated correctly. It needs to be a regular pentagon. period. It is irrelevant that it is inscribed in a circle.. Also, “Insert a pentagon inside a circle” is meaningless as there are infinite pentagons to insert, which should be inscribe.
Here is an interesting extension of the equilateral triangle example that extends the phi cuts with a regular pentagon. https://drive.google.com/open?id=0B86gMl7IvdErVkd4TjJtUE9BY00&authuser=0
1 – phi = 1 / phi
is I guess you’d call one of the “identity formulas” for phi.
If we take the inverse cosine of 1 – phi to get the angle this represents, the answer is
51.827 degrees, which is extremely close to the angle of the sides of the Great Pyramid at Giza, within a few hundredths of a degree.
Something to consider?
Already considered. See https://www.goldennumber.net/phi-pi-great-pyramid-egypt/
Phi angle in the Great Pyramid, is a minimum perimeter triangle:
http://triancal.esy.es/?lang=en&y=2.5980762113533&z=2.5980762113518&p=8.65208917663
Secret rooms are situated in notable points as othocenter:
http://triancal.esy.es/HTML/GG.html?C=0.90455689430153&B=0.90455689430153&a=3.3048039917787&lang=en
hey in this VIDEO >>>>> https://www.youtube.com/watch?v=Sl0BHueSjvA <<<<<>>>3:11<<<<< the golden number in "angle form" whe the ball hits the oobleck! Why? does a hit like that make the air take that "figure" of a flower!! ……. im guessing that every impact behaves that way? if so….. im thinking in adding a little "fixative" in our physics-math proyectile ecuations…………. what do you think????????
jreedxxx7@gmail.com
I’m aware that phi exists in the measurements of a square inside a semi-circle, but can it be found in the measurements of a square inside a circle?
what is the general formula in getting the golden ratio of a building?
To determine the golden ratios found in a building, or in any other object, you can just take one dimension and either multiply or divide it by 1.618. That dimension will be in golden ratio proportion to the original one.
Dear friends
I have published an e-print about constructions of Golden ratio in any triangle.
Please see https://arxiv.org/pdf/1904.02011.pdf
Best regards
Tran Quang Hung.
Hi everyone!
Dear mr. Huang,,
your work seems very interesting from the aspect of research I am envolved in.
If anyone finds it interesting, it is possible to read about it here https://www.atiner.gr/presentations/GEO2019-0139.pdf
According to this, i would ask you mr. Trần Quang Hùng, does these constructions you presented in your work implies some of these values ≈ 22,4555152°, 27,8115295°, 39,7329553°, 46,2983668°, 78,0785741° ?
Looking forward for the response.
Best,
Srđan
p.s. great site, mr. Meisner
Dear Mr Srđan,
Thank you very much for your interest in my paper. You link of pdf file is very interesting. Could we discuss more by email?
My email is tranquanghung@hus.edu.vn
Best regards
Tran Quang Hung.
building a small circular house with golden ratio (from argentina)
hi dear people, im starting a project of building my circular little house here in argentina and would like to learn about the golden ratio for defining the height of the walls and the height and angles of the triangular roof that will sit on those walls for a diameter of a circle of 6.8 meters. im a bit lost, is it posible that the golden ratio to that diameter would be aprox a roof with the highest point in the center of 4.2 meters aprox? any suggestion will be much appreciated. thanks! gera
To keep things in golden ratio proportion, just take any dimension in question and multiply or divide it by 1.618. There are some special triangles with the legs and base in the ratio of 1.618 to 1, so those may be of interest. There is also a golden ratio-based triangle that appears in the dimensions of the Great Pyramid of Giza, so that may be of interest too. See https://www.goldennumber.net/phi-pi-great-pyramid-egypt/. My software site at http://www.phimatrix.com may also give you some ideas.
My simplest method is the equilateral triangle of base 1 unit and height of 1 unit.
Then 1/2 base plus the slant is Phi.
The slant is (1/2) times root 5
Good thought, but that approach only provides some elements related to the golden ratio, but doesn’t provide a construction showing the golden ratio itself.
Well actually, phi can be derived from such a triangle (it is really an isosceles triangle with base = height.)
Half the side (square root of 5 times half the base) gives the circum radius. A line perpendicular to the side one circum radius from the apex meets the meridian of the triangle at the centre of the inner radius. The inner radius is the golden ratio mean of half the base.
Sorry, there was a mistake in my previous comment. The inner radius is down from the apex by the length of the side (which is ths sqrt of 5 times half the base) times phi minus 1. If you bisect the side a line perpendicular to the side meets the meridian of the triangle at the centre of the inner circle.
A triangle with base = height is iscoceles rather than equilateral but such a triagle, where the base=height has an inner radius of 1/phi * base/2. In other words, the inner radius is the phi mean of half the base.
*dreams with the time you find out the answer *
This stuff, the whole hekin page. Absolute fire like totally tetrahedron stuff. Actually after writing that I came to a thought that this is more like Aether level stuff, infinite brilliance the dodecahedron. Thank you for all who are responsible of existence of this domain.
Thanks. You’re very welcome. See the About page for more about the existence of this domain. Regards, Gary Meisner
5. IMPORTANT TO INDICATE THAT IT MUST BE A REGULAR PENTAGON (EQUAL SIDES), JUST LIKE THE TRIANGLE EXPLANATION NOTES THAT IT IS AN EQUILATERAL TRIANGLE. THE SQUARE EXAMPLE IS SELF-EXPLANATORY BECAUSE OF THE DEFINITON OF A SQUARE AS A QUADRANGLE WITH EQUAL SIDES AND EQUAL ANGLES, BUT THIS MUST BE SPECIFIED FOR TRIANGLES AND PENTAGONS.