Phi (Φ) and pi (Π) and Fibonacci numbers can be related in several ways:
 The Pi-Phi Product and its derivation through limits
The Pi-Phi Product and its derivation through limits
The product of phi and pi,
1.618033988… X 3.141592654…, or 5.083203692,
is found in golden geometries:
| Golden Circle | Golden Ellipse |
 | 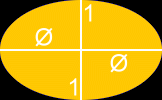 |
| Circumference = p * Φ | Area = p * Φ |
Ed Oberg and Jay A. Johnson have developed a unique expression for the pi-phi product (pΦ) as a function of the number 2 and an expression they call “The Biwabik Sum,”a function of phi, the set of all odd numbers and the set of all Fibonacci numbers, as follows:
| p Phi = 2² {1 | + [ (2/3) / (F1+F2 Phi) + (1/5) / (F3+F4 Phi) – (1/7) / (F5+F6 Phi) ] |
| – [ (2/9) / (F7+F8 Phi) + (1/11) / (F9+F10 Phi) – (1/13) / (F11+F12 Phi) ] | |
| + [ (2/15) / (F13+F14 Phi) + (1/17) / (F15+F16 Phi) – (1/19) / (F17+F18 Phi) ] | |
| – … } | |
| = 5.083203692…. |
This relationship was derived after Oberg noticed an interesting relationship between pi and phi while contemplating geometric questions related to the location of the King and Queen’s burial chambers in the Great Pyramid, Cheops, of Giza, Egypt, the design of which is based on phi.You can access the complete paper published by Ed Oberg and Jay A. Johnson, The Pi-Phi Product, in Word, or the Pi-Phi Product in Excel to see their formulation illustrated numerically.
Trigonometric functions relating phi (Φ) and pi (Π)
Divide a 360° circle into 5 sections of 72° each and you get the five points of a pentagon, whose dimensions are all based on phi relationships.
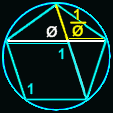
Accordingly, it shouldn’t be too surprising that phi, pi and 5 (a Fibonacci number) can be related through trigonometry:
Or, a much simpler way involving, contributed by Dale Lohr:
Pi = 5 arccos (.5 Phi)
Note: The angle of .5 Phi is 36 degrees, of which there are 10 in a circle or 5 of in pi radians.
Note: Above formulas expressed in radians, not degrees
Alex Williams, MD, points out that you can use the Phi and Fives relationship to express pi as follows:
5arccos((((5^(0.5))*0.5)+0.5)*0.5) = pi
Robert Everest discovered that you can express Phi as a function of Pi and the numbers 1, 2, 3 and 5 of the Fibonacci series:
Phi = 1 – 2 cos ( 3 Pi / 5)
Pi and Phi in the Great Pyramid of Egypt
Another interesting relationship between Pi and Phi is related to the geometry of the Great Pyramid of Giza. This relationship connects dimensions of the Great Pyramid to both Pi and Phi, but it is not known with certainty whether this was an intentional aspect of its design, whether its design was based on Pi or Phi but not both, or whether it is a simple coincidence. It relates to the fact that 4 divided by square root of phi is almost exactly equal to Pi:
The square root of Phi (1.6180339887…) = 1.2720196495…
4 divided by 1.2720196495… = 3.14460551103…
Pi = 3.14159265359…
The difference of these two numbers is less than a 10th of a percent.
See the Phi, Pi and the Great Pyramid page for more details.
Pi squared (Π²) and 987
Pi squared (Π²) is 9.8696…, which, if you round to 9.87 and ignore the decimals, is 987, the 17th number of the Fibonacci series. (Contributed by William Erman.)
More on the relationship of Phi squared and Pi
If you’re looking for other interesting ways to relate pi and phi, 6/5 * Phi^2 = 3.1416, which approximates pi. (Contributed by Steve Lautizar.)

 The Pi-Phi Product and its derivation through limits
The Pi-Phi Product and its derivation through limits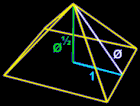


Pi squared (Π²) and 987
Pi squared (Π²) is 9.8696…, which, if you round to 9.87 and ignore the decimals, is 987, the 17th number of the Fibonacci series. (Contributed by William Erman.)
yes as you also can multiply 21 * 13 and add it to 34 * 21 to make 987 which are the number 7th 8th and 9th of the Fibonacci series.
All very fascinating. I would like to connect a few more dots for the community.
.618x.618 ~ .382
360×.382 ~ 137.5
137.5 most prevelant angle of divergence in nature
1/137.5 Fine Structure Constant
137 years old is the most repetitious age in the bible
137 meters Noah’s Ark
137 is the link between science and religion
When I have more time I will return and post more viable information.
Namaste
1 =1God, 3=God, Jesus and Holy Spirit 7=complete number in Bible.
If you go back in time you’ll find that major events or resets happen in sequences of 137 years
Every 138 years, the world in parts, or in a larger scale goes through a cataclysm. So what you said makes sense especially Noah’s Ark and fine structure constant. Are you an Archaix viewer? Incase you don’t know check out Archaix channel on you tube where he explains the return of the Phoenix (Phi) every 138 years the last reset being 1902 and the next one returning May 2040. You can also go back and you will see the events in history. Be careful what you read. Mr J Breshears who started Archaix has read so many ancient books and has worked out after nearly 30 years of study and writing 7 books. There is so love and wisdom in him and he stands in the truth. I highly recommend looking at his work and seeing his wondrous work.
PI = 1.2 PHI^2=3.1416
I found this relationship while studying the work of Rene Schwaller de Lubicz. He had discovered in the measurements of PI and PHI, where both numbers governed it’s PI shape. Over the course of 15 years he measured the Luxor Temple in Egypt and showed that Egypt had a sound knowledge of phi and pi long before the Greeks. Ref his colossal work Temple of Man.
I then found this website as I wanted to delve into the relationship further.
Chris Weismann – which book of Schwaller de Lubicz did you study and where did you get it?
Thank you!
While watching a video on the Pyramids by Samuel Laboy, you can derive the equation 5Pi = 6phi^2 (The same as the equation you presented). Amazing!
These equations relate so well they appear to be Seals, of Creation I find it in the Tetrahedron Cube. This really stumped me because I can’t express in words what I truly see? Do these belong to the Creator YAHUAH 1.618 PHI
& 3.14157 PI belong to the Son YAHUAHSHUA
Who without Him nothing made could be made?
I can Superimpose many many things over these ratios things like Music, Paleo Hebrew language, The Light Spectrum, Sounds & Frequencies, the Soffiegio and Perfect Circle of Sound, also most amazing the Periodic Table of Elements. Am I weird?
No contact me, I share what you vision
Now im interested as well. If you guys could show how ? It will be great
I have also had this vision. I would like to talk about it with anyone that has commented about recognizing the same.
yes, you are connecting the keys to this matrix. any progress on this, anyone?
Look at ThePaulTM on youtube who does dna geometry studies to see how the platonic solids are directly involved in dna. Phi is in dna.
It is simply a mathematical trick. Pi/Phi^2 is 1.199981616… which is close to 1.2, so when you multiply by Phi^2 of course they cancel out and you get Pi.
i noticed that pi x (square root phi)= 4 ( or very close) and you can make a rectangular triangle with sizes phi, (square root phi) and 1, both of a charming simplicity.
From the Giza pyramid one derives the simple relation between pi and phi that is 5/6 of pi minus 1 is phi.
That does provide a close approximation of phi. There are endless variations on that approach though, for instance 4 / square root of phi is close to Pi. They’re all interesting, and many are very insightful and creative, but the most meaningful relationships are those that are exact or that can be related to a geometric construction. See this site’s page on Phi, Pi and the Great Pyramid of Giza for other interesting relationships.
4 (square root of Phi) = 5.088078 which is again close to Oberg and Jonson’s figure above.
Relation of Pi to phi can be
Pi *4/33 =0.3808 = 0.381
1-0.381=.619 =0.618
0.381*2= 0.764
1-0.764= 0.236
What is 4/33?
I noticed whilst writing a program to draw a ‘flower of life’ that the position of the third (and subsequent) circles, after drawing the first two intersecting circles is related by this formula (forgive me, I’m a computer geek, not a math geek) –
Given circles of radius r at co-ords X1, Y1 and X2, Y2, the X co-ord of the center of the third circle, X3 = X1 + ( r / (Pi * Phi) ) * Pi.
Have I restated an existing and known about relationship?
Interesting site by the way. I’ve written a nice Pascals triangle program that shows the relationship between it and prime numbers that you might be interested in. I’ll upload it to my website if you want to have a look.
More easily stated ( I should have noticed earlier) X3 = X1 + R / Phi
Read Liber Primus.
Beware The False Paths.
Good Luck
3301
Hello Cicada,
It is good to hear from you 3301
I have related Phi to Pi and discovered the true nature of the Eye of Horus. I have found your readings and viewed your video (1711141131131). You clearly are on a different frequency and can help me along my quantum physical journey. There is much to discuss.
I would welcome a chance to meet if you. Please send me an email to open a dialogue.
Hello Cicada.
I have read Liber Primus and discovered the secret of the Eye of Horus. I am a young pilgrim who has seen 171114113113.
I am interested in visiting your team in Greenland, if you’ll have me. I think I have novel ideas to lend.
Thank you 3301
we noticed that the circumference of the golden circle isn’t pi but phi*pi and we also discovered that the golden eclipse area is pi*phi and that it isn’t pi.
I am doing 6th Grade Math project on the golden ratio, thanks whoever posted this 🙂
When compared with pythagoras, the angles are 89.1, 31 and 59.9 degrees. Triangle e, phi and pi. Slightly off the 90, 60, 30.
Why???
Maybe calculated on a base of 11 or 9 and not a base of ten???
9/11 mirror numbers. Facebook!
Another trigonometric functinon involving phi is:
2*sin(pi/10) = phi = 0.618033…
notice that pi/10 rad = 18 degrees.
The relation above can be obtained by studying que pentagram or the pythagorean star.
Here is a geometric conversion approximation for pi to phi, exact to ten decimals:
(((4*pi^2)-(pi^3))/2)^(3^-1) = phi + sqrt(10^-13)
This formula shows a counterintuitive result due to the idea that the side areas of a pi cubed structure (4*pi^2) is equivalent to the entire cubic pi volume plus two volume cubes of phi !!?? This equation shows the structure of an elliptic curve:
((phi^3)/(pi^3))-(2/pi)+(1/2) = .00000008013
In the elliptic curve equation, (x^3)+(y^3) = 4*x*y, the xy point, parallel to the x axis tangent point of the elliptic cusp curve generated by the latter equation is, x=1.67894731 , y=2.1165347, can be substituted for x:phi and y:pi, respectively.The interesting thing about surface areas being greater than the sum of cubic volumes is this effect happens to black holes, where 1/4 of the surface area of a black hole contains more information than the entire volume of the black hole!?
Where did you come up with this reference – or did you devise it yourself.
It is very interesting, The only similar reference I can find on the internet to it
is in this pdf.
https://cims.nyu.edu/~kiryl/Calculus/Section_2.6–Implicit_Differentiation/Implicit_Differentiation.pdf
I link to the reference is posted here in this image.
https://cloudup.com/cjtHpKgbvWx
Pleasing to “see” you again J.Juliano
A few approximations with regard to Phi and Pi are as follows:
Whilst the Great Pyramid of Giza dimensions are: 756 base side length and a height of 480 the volume will be: 480 x 756 x 756 ÷ 3 = 91445760. The base perimeter will be: 756 x 4 = 3024, the square root of the volume of 91445760 = 9562.727644349… this divided by 3024 = 3.162277660168379… this is the √2 x √5
Hence the Great Pyramid as a “cube” is: 480 x 756 x 756 = 274337280 the square root of this is 16563.1301389… this divided by 3024 = 5.4772255750516… this is the √2 x √5 x √3, in view of the fact that the 16563.1301389…÷ 9562.727644349…= 1.732050807568… which is √3
Into a good quality calculator 1836 afterwards click Cos to obtain: 0.8090169943749…this multiplied by 2 = Phi
Likewise the Great Pyramid 756 Cos. x 2 = 1.61803398874989…this is Phi
Likewise the Great Pyramid 480 Sine: x 2 = 1.732050807568877…this is √3
The Canonical Earth mean circumference is: 131383296, feet The Maya super number: 1366560 is 5256 {Maya Tzolkins} multiplied by 26
The 131383296 reduced to 131.383296 plus 0.78 then divided by 26 = 5.083203692307 although we observe a cyclic 692307 we discover that: Phi x Pi = 5.08320369231…
Consequently 5.083203692307 is Phi x 3.14159265358…which is Pi correct to 11 decimal places
Therefore 5.083203692307 is Pi x 1.61803398874…which is Phi correct to 11 decimal places
Peace
Derek
Is it possible that ancient mathematicians knew something we don”t? I’m just in 8th grade trying to understand all of this.
addendum: y in the elliptic curve is actually rewritten to the fraction 8/3=2.6666…
PLEASE REF. links found in Web Side http://www.stefanides.gr:
http://www.stefanides.gr/Html/QuadCirc.htm
http://www.stefanides.gr/Html/piquad.htm
http://www.stefanides.gr/pdf/GOLDEN_ROOT_SYMMETRIES_OF_GEOMETRIC_FORMS_by_Panagiotis_Stefanides.pdf
In the section “Trigonometric functions …”, I find the first note incorrect. It should read: “Note: The angle of Pi/5 is 36 degrees, of which there are 10 in a circle or 5 in Pi radians.” and not “Note: The angle of .5 Phi is 36 degrees, …”
Saying π/5 = 36 degrees says little, knowing that 2π is 360.
I think it points to:
cos 36 = φ/2
This means that the ONLY reason we can divide a circle into even 5ths is because of φ. Or at least, if you divided a circle into perfect 5ths, then you must have used φ, even if you didn’t realise.
Jeff, I’d say that this is the best and most fitting relationship of pi and phi I read here! Thank you for sharing, now, I feel enlightened! No vague lalala – thank you
I noticed that a
near perfect 7 sided figure, a heptagon with an angle of
can be constructed from any arm of the
5 pointed star.
http://i761.photobucket.com/albums/xx255/paldenium/image.jpg1_12.jpg
which seems to reflect the
phi=7/5 (Pi/e)
similarly
http://i761.photobucket.com/albums/xx255/paldenium/image.jpg1_14.jpg
the base cuts the points at 1:phi
1.618018
Thanks to Marcus the Maronite and Hirano
The area of the golden ellipse is simply the pi-phi product multiplied by the square of the semi-minor axis. The convergent of this product with 22 continued fraction values is [5; 12, 53, 2, 14, 1, 1, 4, 2, 5, 11, 3, 11, 3, 1, 4, 4, 17, 1, 45, 5, 2].
I observed that Pi/2 = atan(1/sqrt(phi)) + atan(sqrt(phi)).
Read about it in…
https://jorgexerxes.wordpress.com/2015/07/16/algumas-relacoes-matematicas-entre-a-constante-pi-a-razao-aurea-e-a-construcao-de-piramides/
That is true, as it is derived from the triangle shown in the article with sides of the sqrt of Phi and 1, with a hypotenuse of Phi
1/sqrt(phi) = 0.786151377757423
sqrt(phi) = 1.272019649514070
atan(1/sqrt(phi)) = 0.666239432492515
atan(sqrt(phi)) = 0.904556894302381
Total = 1.570796326794900
Pi = 3.141592653589790
Pi/2 = 1.570796326794900
Pi and Phi can be also related through trigonometry through angles involving the pentagon that divides a circle in five sections.
Beware though of articles that tell you that Pi * Sqrt (Phi) = 4. That is not true.
And that is precisely what PANAGIOTIS STEFANIDES
(https://www.goldennumber.net/pi-phi-fibonacci/#comment-1759)
is trying to claim for fame and he has gone to extensive lengths to prove the clever paradox that π = 4/√φ based on kepler triangles and that this erroneous
value of π is the correct one, Along the lines he makes the extraordinary claim that some aliens in fact notified mankind about it.
Read a little about it here but don’t laugh please
:
http://www.veteranstoday.com/2015/10/06/pi2/
Hi Gary and Khalfan,
Thanks for replying and for your reading suggestions!
I developed a little bit more and prepared two another posts.
Note that, despite of some Math and Physics, the main purposes are Art and Aesthetics.
https://jorgexerxes.wordpress.com/2015/11/12/orbit-study/
https://jorgexerxes.wordpress.com/2015/11/24/cosmological-study/
Best Wishes!
The angle of 0,5 x 1.618 x (57.3 deg/rad) = 46.36 degrees not 36 degrees.
If we multiply Phi by 2/5 or 0.4, we get:
0.4 x 1.618 x (57.3 deg/rad) = 37.08 deg, which is not 36, but certainly closer.
There is no reason why 360 should be related to Pi or Phi, since it was only picked because it was divisible by so many factors (2, 3, 4, 5, 6, 8, 9, 10, 12, 15, 18, 20, 24, 30, 36, 40, 45, 60, 72, and 90).
If we search for inter-relationships of 360 with e, Pi, or Phi, we’ll find some but they will be only coincidental, with no native meaning.
Hi
cos (pi/5) = phi/2
“There is no reason why 360 should be related to Pi or Phi”
cos (pi/5) = phi/2
And yet it is. The relationship is related to the geometry of triangles which divide a circle into 5 parts. The pentagon is based on this geometry, and all its segments are in golden ratio proportion to the others. See more at https://www.goldennumber.net/geometry/.
no, it’s not. 360 is a completely arbitrary number. “5” is the number related to Φ… dividing a whole into 5 parts creates Φ ratios. If we as humans had decided that circles have 500 degrees, then the number 100 would be significant. Also, to whomever posted the relationship between pi^2 and 987, this is not significant. Yes, 987 is the 17th number of the fibonacci sequence. Yes ignoring decimal places in base(10), pi^2 is ~ 987. But 100 is an arbitrary number in any other base. I could argue that written in base(12), this no longer matters or holds true.
But in base 12, Φ can not be written as a function of “fives.”
The relationship cos(pi/5)= Φ/2 makes relative sense. Φ is related to the functions 2x and 0.5x (and other binary operations using these functions as parameters). pi/5 in radians represents 1/5 of a semicircle circle, and as such, it makes sense that the cosine of 1/10 a circle is equal to half of Φ. Again, this is not a true relationship between Φ and pi because 2pi is an arbitrarily chosen number which represents the whole of a circle, just like 360 degrees.
Can you explain what you mean by “true relationship” with some exemples ?
If you think 360 degrees in a circle is arbitrarily chosen then I’m afraid you’re missing out on some very interesting information
I think 360 degrees in a circle is arbitrarily chosen but it is a judicious choice . 400 grades was another choice less judicious .
Hello,
please find enclosed a small treatise concerning squaring the circle.
http://www.gurt-der-wahrheit.org/files/quadratur_des_kreises.pdf
.. Although only in German, but the pictures say more than 1000 words … 🙂
Kind regards,
Gerhard Dnaiel Kadisch
http://www.gurt-der-wahrheit.org
I’m tired of these approximations… 3.1446 is NOT pi.. so stop posting this nonsense unless you have some real valid equations
Approximations is all there is because math does not depict reality and its foolish to think it does.
According to google,; earth’s circumfrence = 24901
Earths radius = 3959
Solve for pi… you get 3.1448
So, this concept of 3.14159265… going on forever is stupid… plus the proof of this number involves infinity so it can not be correct
If anything it is 3.1416, and thats it… but this only works mathematically, yet practically for true values and distance the first figure is much more accurate
Right on! Saying that something IS the same thing as something similar is as irrational as pi itself
Over the floor is an Isosceles triangle with two equal heights and minimum perimeter: That gives two equal angles 51.8272923729º in the base whose cosine is 0.6180339887=Phi–1 proportions that we can find in the Great Pyramid of Giza transversal section. Angles formula in radians: COS(A)+COS(1)=COS(B)+COS(C)
Obtain it with TrianCal: http://triancal.esy.es/?lang=en&y=314.460551103&z=314.460551103&p=1047.2135955
Dear Sirs,
Could You, please, evaluate this Idea?
https://jorgexerxes.wordpress.com/2017/08/22/how-to-nullify-gravity/
Thanks In Advance!! Jorge Xerxes
Phi^2=phi+1
Phi^3=2phi+1
Phi^4=3phi+2
Phi^5=5phi+3
Phi^6=8phi+5
….etc….
Here we can notice the Fibonacci sequence
Place phi into the “mandelbrot” set.
See in the drawing two structures of Pi () over Sin; Tan; Phi-1 and Fibonacci divisions.
Kind regards, Gerhard Daniel Kadisch.
here as PDF
http://www.gurt-der-wahrheit.org/files/Pi()%20durch%20Sin%20Tan%20und%20Fibonacci.pdf
and here the DWG-File:
http://www.gurt-der-wahrheit.org/files/Pi()%20durch%20sin%20Tan%2036%c2%b0%20und%20Fibonacci-2.dwg
This topic is very interesting. My background is engineering, not mathematics. Yet the combined representation of the relationships among pi, phi, and the fibonnaci series through fornula, geometric and numerical methods are both understandable and elegant. I believe this is novel and significant and presents fundamental insights that could lead to a new unifying paradigm relating mathematics and our world view.
Real value of π = 3.1446055110296….. = 4/√ϕ
This can be expressed as
π⁴ + 16π² =16²
This debate over the real value of pi is very interesting. I’ve seen a variety of proofs presented, but no one has really explained why the many methods that can be used to calculate the commonly accepted value of pi are wrong. That needs to be addressed with great detail and clarity in order for this claim to be accepted. I’m willing to post them on this site if they’re good.
A close relationship between π and φ, in case no one has noticed it yet, is
φ^39 ~ π^17/2
An even closer relationship is
φ ~ (π/2*(π^16 + 19√2))^(1/39) = 1.6180339887500868…
( φ = 1.6180339887498948… )
But when it’s just an approximation and not exact we have to ask the question if it’s truly a relationship. With more numbers and complicated formulas we can achieve more significant digits of accuracy, but that can be done with any set of two numbers. How does that demonstrate “relationship” versus just creative expression of mathematics?
Not a good choice of words, I admit. Near-identity might have been better. That’s what those are, just approximations due to fortuitous coincidences. You are right: “relationship”, close or not, would imply a mathematical connection between both constants. Clearly not the case here.
φ = e^(iπ/5) + e^(-iπ/5)
Says: Phi is the displacement between one 10th of a clockwise and counter clockwise rotation along the unit circle.
or.. Phi is a chord 1/5th along the unit circle.
HI friends, i am not “Educated” as some if you but i found these numbers ,
While playing around for fun with some Calculations/Sequences I found these Decimals/Fractals ?(:
Phi= 1.61803398
Pi= 3.141 Pi x Phi =
5,082399953118 and when searched on Google it got 0 results? The Result is aligned with Fibonacci seq/numbers?
i found E to work better in this way. e= 2,71828182 or 2,71828182845904
Phi = 1.61803398
Pi = 3.141592653
E = 2,718281821
Phi^2 = 3Gc/pi x a, where G is the gravitational constant, c = speed of light, and a = fine structure constant. This expression is also equivalent to 6a^2 x h/pi x e^2, where h = Planck constant, and e = elementary charge (electron or proton).
You can see more on my paper at vixra.org/abs/1803.0290
you all need to see this: http://measuringpisquaringphi.com/
https://www.youtube.com/watch?v=2fS9ixfQ_no
Check this out, especially the ending.
Pi must be the ratio of the radius of the smallest thing to its circumference: at the speed of light all things must be massless dots without any discernible properties. Which means that as one would decelerate there would be a relative region where the characteristics of an object were blurred before the ratio of pi were visible.
Wavelength, divided by the Planck length, L/ℓ P=pi*phi
Math is fun
Sir,
I have recently published a paper that reveals THE EXTREMELY PRECISE Pi:Phi CORRELATION, which is firmly premised upon Classical geometric principles.
Video Link: https://youtu.be/P1Ddz55JFlc
Paper Link: https://rajpub.com/index.php/jam/article/view/8498
Extremely precise Pi:Phi Correlation
https://rajpub.com/index.php/jam/article/view/8498
If you do 6/5*Phi^2 you get 3.1416407865 as established above.
6/5 ⋅ 2.61803398875 = 3.1416407865
But… If you do 3.1416407865 and divide it by 432 (Hz.???), you get a fairly close approximation of the fine structure constant α = 0.007297352566.
3.1416407865 / 432 = 0.007272316635
If you multiply that 0.007272 (the true result) by 360, you get back to Phi^2.
0.007272316635 × 360 = 2.61803398875
If you do twice the square root of Phi^2, we get 1.27202.
√(√2.61803398875) = 1.272019649514
If a square is related to the base of a Kepler’s right triangle, which is the model for half of one face of the Pyramid of Giza, then the height of that triangle HAS to be 1.27202 times greater in order to uncover the true Pi.
Equation for Kepler’s Right Triangle is exactly the same as Pythagoras’ Theorem where the base is one and the height is 1.27202:
√(1² + 1.27202²) = 1.618034 (Phi is the Hypotenuse).
In other words, 4/1.27202 = 3.14460551103 is the true Pi. Here’s how and why:
When taking the square area of 4 and divide it by 3.14460551103, then square the result to thereafter subtract 3.14460551103 from the result, the answer gives you a perfect 16. If you are confused, here’s a better way to compare it:
With traditional Pi – >
((4² / π)² − π²) = 16.068619
With True Pi – >
((4² / (4 / 1.27202))² − (4 / 1.27202)²) = 16
So there is an absolute relation between the following numbers: Reduced Pi (3.1416407865), Increased Pi (3.14460551103), Phi (1.61803398875), 4 (square), 5 (Pentagon), 6 (Hexagon), 432 (Hz), 360 (degrees) as demonstrated here:
(√(1/(√(((6/5 ⋅ ((1 + √5) / 2)²) / 432) × 360))) × 4) = 3.14460551103
Hi Gary, on the ninth of this month June 2021 I came up with two approximations for the A.U. values of Venus and Mars such that there is a connection between Phi and Pi. Venus is then .723305077 and Mars 1.523719184 Then give mars the music interval 1.875 as a power and devide it by the 1.875 root of Venus which equals Phi squared and then Mars to the power I.875 times Venus to the power 1.875 times Phi squared equals Pi. N.A.S.A gives the values as .72332102 for Venus and 1.52371243. All the best John Shanahan.
If one puts the following into google the A.U values for mars and venus are to be found at the bottom of the page. JPL Orbital Elements 3000 BC to 3000 AD
Thanks a million Gary!
A previous post of mine:{today is 28/06/2021
Derek Skhane says
November 27, 2016 at 11:21 am
Pleasing to “see” you again J.Juliano
A few approximations with regard to Phi and Pi are as follows:
Whilst the Great Pyramid of Giza dimensions are: 756 base side length and a height of 480 the volume will be: 480 x 756 x 756 ÷ 3 = 91445760. The base perimeter will be: 756 x 4 = 3024, the square root of the volume of 91445760 = 9562.727644349… this divided by 3024 = 3.162277660168379… this is the √2 x √5
Hence the Great Pyramid as a “cube” is: 480 x 756 x 756 = 274337280 the square root of this is 16563.1301389… this divided by 3024 = 5.4772255750516… this is the √2 x √5 x √3, in view of the fact that the 16563.1301389…÷ 9562.727644349…= 1.732050807568… which is √3
Into a good quality calculator 1836 afterwards click Cos to obtain: 0.8090169943749…this multiplied by 2 = Phi
Likewise the Great Pyramid 756 Cos. x 2 = 1.61803398874989…this is Phi
Likewise the Great Pyramid 480 Sine: x 2 = 1.732050807568877…this is √3
The Canonical Earth mean circumference is: 131383296, feet The Maya super number: 1366560 is 5256 {Maya Tzolkins} multiplied by 26
The 131383296 reduced to 131.383296 plus 0.78 then divided by 26 = 5.083203692307 although we observe a cyclic 692307 we discover that: Phi x Pi = 5.08320369231…
Consequently 5.083203692307 is Phi x 3.14159265358…which is Pi correct to 11 decimal places
Therefore 5.083203692307 is Pi x 1.61803398874…which is Phi correct to 11 decimal places
Peace
Derek
Reply
(e^(4/3))/(EM^6)/64/((pi/3)^3)…the reciprocal log e of this equation =1/3.
Where e=2.718281828.
.EM=.577215665….
Golden Ratio, Metallic Means and Pythagorean Triples
https://youtu.be/LFW1saNOp20
The orbital period of Venus, the planet associated with beauty is ~224.65 days.
The orbital period of the Earth is ~365.2425 days (according to the Gregorian calendar).
224.65 / 365.2425 = 0.615070809 Pretty close to Phi’s 618.
Keep in mind that orbital periods are approximations.