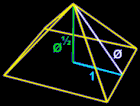
Phi (Φ) the Golden Section, has been used by mankind for centuries in architecture.
Its use started as perhaps early as with the Egyptians in the design of the pyramids. When the basic phi relationships are used to create a right triangle, it forms the dimensions of the great pyramids of Egypt, with the geometry shown below creating an angle of 51.83 degrees, the cosine of which is phi, or 0.618. (See more on this at Phi, Pi and the Great Pyramid of Giza and Golden ratios in Great Pyramid of Giza site topography.)
The Parthenon
The ancient Greek Euclid ((365–300 BC) wrote of it in “Elements” as the “dividing a line in the extreme and mean ratio.” The Parthenon, built in 447 to 438 BC, appears to use it in some aspects of its design to achieve beauty and balance its design. The illustration below shows one of the ways that the golden ratio is often reported to appear in its design. This, however, is subject to some debate, as the application of the golden ratio is often not accurately described in many sources. Furthermore, using the second step of the Parthenon seems somewhat arbitrary. There are, however, other dimensions of the Parthenon which appear to be golden ratios. This is discussed in more detail at The Parthenon and the Golden Ratio.

Notre Dame
Notre Dame in Paris, which was built in between 1163 and 1250 appears to have golden ratio proportions in a number of its key proportions of design. Although it is rather asymmetrical in its design and difficult to measure photographically because of parallax distortions, the golden ratio lines of the green, blue and red rectangles conform closely to the major architectural lines, which represent:
- Red – Vertical height of base at ground level : Top of first level : Top of second floor
- Blue – Vertical height of base of second level : Top of second level : Top of third level
- Green – Horizontal width of outside of left top section : Inside of top right section : Outside of top right section:

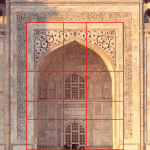
The Taj Mahal
Renaissance artists of the 1500’s in the time of Leonardo Da Vinci knew it as the Divine Proportion. In India, it was used in the construction of the Taj Mahal, which was completed in 1648. Click on photos below for enlarged image.
The United Nations Secretariat Building
The United Nations building also reflects the golden ratio in a number of aspects of its design, as described in more detail on the UN Secretariat Building page.
- UN Secretariat window configuration reveal golden proportions
Toronto’s CN Tower
The CN Tower in Toronto, the tallest tower and freestanding structure in the world, has contains the golden ratio in its design. The ratio of observation deck at 342 meters to the total height of 553.33 is 0.618 or phi, the reciprocal of Phi!

Thanks go to Moein Danesh for the contribution of information on the Taj Mahal and to John Owen for his contribution of this information on the CN Tower








It’s incredible! We are searching for sophisticated solutions, and invite new ways to build higher, and more magnificent buildings, where even our predictors knew simplest and most practical rules even used today… I think we should go back to our roots. Regards. Dom
I urge you to watch The Revelations of the Pyramids (YouTube) – a fantastic insight into the amazing pyramids in Egypt, Peru, Mexico and China (YES China !!??) It’s about 100 mins long but such compelling viewing it goes very quickly. The Pi and Phi usage and the generall feat of the constructions is mind blowing! I hope you enjoy! Regards, Wal
yes awesome, fascinating how the Egyptian pyramids and the Mayan step pyramids are similar, did you ever watch The New Chariots of the Gods on youtube, with Von Danikan, it’s like the Mayan pyramids have the same kind of astrological design incorporated into it that displays only at the equinox!!! on the other side of the world!!!:)
Thanks, Wal, for your recommendation on Revelation of the Pyramids. Very fascinating. It lead me to add a page to the site on Phi and Pi in the dimensions of the Great Pyramid of Giza in Egypt.
Thank you everyone, for mentioning this video as I’m watching it now. I’ve never heard of the golden ratio before & it’s intriguing.
Yea
When carpenters are building stairs there is a general rule that they follow in order to build a comfortable set of stairs. If you add the rise of the stair to the length of the run ( in inches ) you should get close to eighteen. A very nice rise ( especially for older folks ) is 6 3/4″ . Combine that with an 11″ run and you have a very comfortable set of stairs. 11 divided by 6 3/4 is 1.629… VERY close to PHI! This makes sense since the human body has the phi ratio all over it.
close to phi is not phi
That’s true, but from a practical viewpoint an 18″ run would result in a run of 11.1246118…” and a step height of 6.875388203…”, and no carpenter is going to be that precise. Note how the following more realistic options produce a result that illustrates a phi relationship:
Step Run Ratio
7.000 11.000 1.571
6.875 11.125 1.618
6.750 11.250 1.667
Oh, but carpenters do aim for perfection (I’m a master carpenter), but are often dictated to by existing or architectural designs to adjust their stairs to the space allocated. I was taught early on that the ideal rise and run of stairs equal 18″. Interestingly, a standard 2×12 measures 11.25″, and is the norm for stair treads. A standard 1×8 (typically used for risers) measures 7.25″. That allows 1/2″ to tuck in behind the back edge of the tread. It also allows for adjustment of the rise should there be less than optimal total run space available in any given structure. The point is, 18 is the guide.
great great great info for projects and reports.
does anyone more names of buildings with the golden number? thanks
incredible
These images are showing best examples of good architectural designs. I am very impressed with these images.
is the ratio 0.618 or 1.618
Either is correct, depending on the application as they are reciprocals of one another. If the ratio of the larger to the smaller is 1.618, then the ratio of the smaller to the larger is 0.618. 1.618 is often denoted as Phi with a capital “P” while 0.618 is denoted as phi with a lower case “p.”
I am an architect student in year 2. I am curious about the golden ratio. what is exact meaning of it? Could you give me more example or explain more about it?
For examples of applications of the golden ratio, see the PhiMatrix design applications page.
wow i don’t want to do math ever again
Brocco, I agree with you.
Great buildings!
I’m not buying into the “fact” that everything in nature is fractally composed of fractals.
Nor do I see the relevance of a few buildings which many will claim have no relationship to Phi.
I call pseudoscience, sorry Gary.
Some may claim that the buildings have no relationship to phi, but then where are their measures and evidence? You can’t just “refute” and “call pseudoscience” without presenting evidence to the contrary and then call it “science.” The images presented here and on the other pages referenced on the site give examples of golden ratio proportions. No statement is made that everything in nature is in golden ratio proportions either, but rather that it appears so commonly as to not be chance. Also, no “science” is implied in the application of phi to architecture. It’s just an artistic design choice to use proportions commonly found in nature and basic geometry, and that for those reasons appear natural and pleasing.
Does the Golden Ratio have any value for creating structures with durability? Sure, it looks pretty, but does it make things last when compared to other ratios?
Dear Jacob,
I would like to say yes, from my understanding of ‘Sacred Geometry’..there is always something so special with the ratios of let us say the ‘Divine Proportion’ The smallest point is indicative of the Highest point. And therefore one asks …what is the microcosmic/macrocosmic relationship. One particular answer is as it were the Alpha and the Omega. We are dealing a sbject on an eternal level…if that is purely a conceptional view point or simply philosophical, I would suggest that it so important to bring into one’s equation of understanding that we can be dealing something so very real…that it is the unknown reality it’self and that the cosmos and life on earth is so valuable. It makes me wonder how it is possible to be as synic..not saying that you are …just saying that there is a great wonder to be deeply respcted universaly but in todays times on earth even so most importantly.We need to value nature on a level such as is so importantly required today and also that is of..as it were not just human life but that of all creation and hopefully..no more fracking..God bless take care.. I hope we will all come more sensitivity to this very wonderful ‘world’ – enviroment that we do need to take care of–many blessings..all the best William
Dude
Hello… I’m an student of architecture. thank you for sharing this information. I’m very inspired with Golden Ratio and I want to use it in my design problem as a concept. Do you have some more information regarding this. How to use Golden ratio in buildings.?
What is the relation between( phi-golden ratio)
Just different names for the same thing. The Greek letter Phi represents the number 1.618…, just like Pi represents the number 3.14… This number is also known as the Golden Ratio/Mean/Section/Proportion or the Divine Proportion.
I’d like to be so good architect like this who designed the Notre Dame.
thank you for the image of the golden section, this is my first time of hearing it. I’m architecture student.
..the first dodecahedron building in the world (according by Google) is made by http://www.smartdome.si in Slovenia/Krško… see the proces of building on fb pages..the whole project is made by golden ratio proportions..
As a student of architecture in high school, I was very much interested in the proportions of design, obsessed that buildings be symmetrical or aesthetically pleasing with no prior knowledge of golden ratios or proportions. Is it possible that humans and any other animal that creates shelter for himself does it in a way that is intrinsically proportional or built in a way that reflects the innate ability to produce such “geometrical patterns” or includes the concepts of the golden ratio, Fibonacci or proportions without any awareness of doing so?
Explore perfect spirals in nature. Seashells and certain types of flowers contain perfect spirals which can be constructed from rectangles using the golden ratio. Happy hunting!
This requires a bit more explanation. Spirals in nature are typically logarithmic (aka equiangular or exponential) spirals, which by themselves have nothing to do with the golden ratio. A golden spiral is just a very special case of a logarithmic spiral that expands at a constant rate based on the golden ratio rather on some other ratio. So by analogy, while gold is a metal, not all metals are gold. And technically speaking, connecting the arcs of the golden rectangles creates a spiral known as a volute, which is ever so slightly different than a true equiangular spiral. And the spirals found in plants, such as those in pine cones and seed pods, are based on successive numbers in the Fibonacci sequence. The ratios of Fibonacci numbers converge on the golden ratio as you go further in the series, but are not exactly the golden ratio. See more on this here:
https://www.goldennumber.net/spirals/
https://www.goldennumber.net/nautilus-spiral-golden-ratio/
https://www.goldennumber.net/plants/
Amazing buildings with breathtaking views
Great article! Amazing how much work and passion was put into these buildings.
I found this site quite useful for my maths assignment on THE GOLDEN RATIO
Im really intrested how the hell Egyptians could measure the phi with some sticks and ropes on the sand or papyrus…. It’s irrational! How Egyptians could know about such constants?
Once you understand how simply and pervasively the golden ratio appears in geometry, the better question is how could they not have come across it. They didn’t have to know about irrational constants. All they needed to know was some simply geometric constructions. See https://www.goldennumber.net/geometry/ and the section titled “Many basic geometric constructions create golden ratio proportions” at https://www.goldennumber.net/golden-ratio-misconceptions-by-george-markowsky-reviewed/.
I think it is also worth noting just how mathmatically perfect this number is. The exact number comes from taking the square root of 5 then add 1 and then divide by 2. The number rounded off is 1.618 but is non recurring. Now what is amazing is that if you square this number the decimals do not change, if you take the inverse the decimals do not change. This is the perfect number and appears in many mathmatical series like Fibinacci. The face that the ratio is present in nature is the beauty.
Once you understand how simply and pervasively the golden ratio appears in geometry, the better question is how could they not have come across it.
Hello. Have you analyzed Greek Key borfders? I’m actually most interested in how they originated and if the geometric repetition to “infinity” held any special significance in the Ancient Greek mind. With Thanks
I’ve not analyzed Greek key borders. From the ones I just examined, it appears that the proportions of their lines are based on integer relationships, not the golden ratio or other geometric progressions.
thank you. now i have known.