The dimensions of the Earth and Moon are in Phi relationship, forming a Triangle based on 1.618.
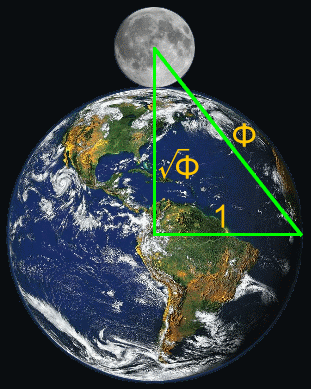
The illustration shows the relative sizes of the Earth and the Moon to scale.
- Draw a radius of the Earth (1).
- Draw a line from the center point of the Earth to the center point of the Moon (square root of Phi).
- Draw a line to connect the two lines to form a Golden Triangle (Phi).
Using dimensions from Wikipedia and geometry’s classic Pythagorean Theorem, this is expressed mathematically as follows:
| Dimension (km) | Proportion (Earth=1) | Mathematical Expression | |
| Radius of Earth | 6,378.10 | 1.000 | A |
| Radius of Moon | 1,735.97 | 0.272 | |
| Earth + Moon | 8,114.07 | 1.272 | B |
| Hypotenuse | 10,320.77 | 1.618 (Φ) | C, where C²=A²+B², so C=√(A²+B²) |
| Hypotenuse² / (Earth Radius + Moon Radius)² | 1.618 (Φ) | C²/B² |
Another way of looking at the relationship is to take 10320.77² / 8114.07², which is 106,518,293.39 / 65,838,131.96, which rounds to 1.618. The calculation to 6 significant digits is 1.61788…, which is different from 1.61803… by only 0.0009%.
This triangle is known as a Kepler triangle. This geometric construction is the same as that which appears to have been used in the construction of the Great Pyramid of Egypt.
Source: Hidden Nature by Alick Bartholomew. Thanks to Sathimantha Malalasekera for bringing this to my attention.
Certain solar system orbital periods are closely related to phi
 Certain planets of our solar system seem to exhibit a relationship to phi, as shown by the following table of the time it takes to orbit around the Sun:
Certain planets of our solar system seem to exhibit a relationship to phi, as shown by the following table of the time it takes to orbit around the Sun:
| Mercury | Venus | Earth | Jupiter | Saturn | |
| Power of Phi | -3 | -1 | 0 | 5 | 7 |
| Decimal Result | 0.24 | 0.62 | 1.0 | 11.1 | 29.0 |
| Actual Period | 0.24 | 0.62 | 1.0 | 11.9 | 29.5 |
Saturn reveals a golden ratio phi relationship in several of its dimensions

The diameter of Saturn is very close to a phi relationship with the diameter of its rings, as illustrated by the green lines. The inner ring division is in a relationship that is very close to phi with the diameter of the rings outside the sphere of the planet, as illustrated by the blue lines.The Cassini division in the rings of Saturn falls at the Golden Section of the width of the lighter outside section of the rings.
Note: Phi grid showing Golden Ratio lines provided by PhiMatrix software.
A closer look at Saturn’s rings reveals a darker inner ring which exhibits the same golden section proportion as the brighter outer ring.

Venus and Earth reveal a golden ratio phi relationship
Venus and the Earth are linked in an unusual relationship involving phi. Start by letting Mercury represent the basic unit of orbital distance and period in the solar system:
| Planet | Distance from the sun in km (000) | Distance where Mercury equals 1 | Period where Mercury equals 1 |
| Mercury | 57,910 | 1.0000 | 1.0000 |
| Venus | 108,200 | 1.8684 | 2.5490 |
| Earth | 149,600 | 2.5833 | 4.1521 |
Curiously enough we find:
Ö Period of Venus * Phi = Distance of the Earth
Ö 2.5490 * 1.6180339 = 1.5966 * 1.6180339 = 2.5833
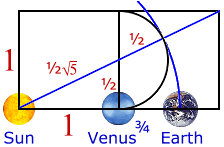
In addition, Venus orbits the Sun in 224.695 days while Earth orbits the Sun in 365.242 days, creating a ratio of 8/13 (both Fibonacci numbers) or 0.615 (roughly phi.) Thus 5 conjunctions of Earth and Venus occur every 8 orbits of the Earth around the Sun and every 13 orbits of Venus.
Mercury, on the other hand, orbits the Sun in 87.968 Earth days, creating a conjunction with the Earth every 115.88 days. Thus there are 365.24/115.88 conjunctions in a year, or 22 conjunctions in 7 years, which is very close to Pi!
See more relationships at the Solar Geometry site.
Relative planetary distances average to Phi
The average of the mean orbital distances of each successive planet in relation to the one before it approximates phi:
| Planet | Mean distance in million kilometers per NASA | Relative mean distance where Mercury=1 |
| Mercury | 57.91 | 1.00000 |
| Venus | 108.21 | 1.86859 |
| Earth | 149.60 | 1.38250 |
| Mars | 227.92 | 1.52353 |
| Ceres | 413.79 | 1.81552 |
| Jupiter | 778.57 | 1.88154 |
| Saturn | 1,433.53 | 1.84123 |
| Uranus | 2,872.46 | 2.00377 |
| Neptune | 4,495.06 | 1.56488 |
| Pluto | 5,869.66 | 1.30580 |
| Total | 16.18736 | |
| Average | 1.61874 | |
| Phi | 1.61803 | |
| Degree of variance | (0.00043) |
Note: We sometimes forget about the asteroids when thinking of the planets in our solar system. Ceres, the largest asteroid, is nearly spherical, comprises over one-third the total mass of all the asteroids and is thus the best of these minor planets to represent the asteroid belt. (Insight on mean orbital distances contributed by Robert Bartlett.)
2005 unveiled the discovery of a 10th planet called 2003UB313. It was found at a distance of 97 times that of the Earth from the Sun. Its ratio to Pluto would thus be 2.47224, much higher than any previous planet to planet orbital distance ratio. Could it be that this is actually the 11th planet and the 10th planet will be found at an orbit whose ratio is 1.52793 times that of Pluto, preserving the phi average? Time will only tell, but if it happens remember that you heard it here first.
The shape of the Universe itself is a dodecahedron based on Phi
New findings in 2003 based on the study of data from NASA’s Wilkinson Microwave Anisotropy Probe (WMAP) on cosmic background radiation reveal that the universe is finite and shaped like a dodecahedron, a geometric shape based on pentagons, which are based on phi. See the Universe page for more.



This is just WOW!
how does saturn cast a shadow on its rings
The rings encircle Saturn, so the section for which the planet’s body blocks the sunlight is in the shadow. On Earth, we most often see Saturn slightly from a side angle due to our rotation around the sun, so we get a glimpse to the back side of the rings that are in that shadow.
Do you know golden point on earth!!
It is Holy Kaaba in Mecca ……watch it on youtube…!
And see the article and discussion on it on this site at “The Golden Ratio Point of the Earth.”
Well if true it has moved. The North Pole is now over Russia land in Siberia and it has moved considerably. This means there is a new location for the Golden point on Earth, probably S.W. of Mecca I am sure someone has tracked it?
You mean our Earth is tilted more than it was ?
It is so small that even after centuries, the Golden Ratio Point will even be inside the circumference of the HOLY KAABA !
The pole is based on the axis of the Earth’s rotation, which is independent of the tilt of that axis from perpendicular to the Earth’s orbit.
But the HOLY KAABA?!
We know that the ancient Persians, and Egyptians, were both great Astronomers, Mathematicians & into Holy Architecture and Sacred Geometry.
The vesica piscis and flow of life on the walls of Ancient Egypt’s monuments, & the ratio and design of the Great Pyrmamid is just kind of mindblowing. Very advanced.
That it’s also encoded into the Moon-Earth-Sun geometrical relationship, for REAL, is just amazing amazing amazing (no words) because it reveals that our Earth is somehow a place that’s both “signed” by the Creator & that houses His creation of man in His image.
The ancient Egyptians seemed to understand this, & I do believe also that certain signs and configurations, including a blood red moon lunar eclipse on April 3rd, 33AD framed the birth life and Great Work of Jesus Christ son of God, so I point to Golgotha and to a place near the Holy Kaaba.
Oh what is man that thou art mindful of him?
Great thoughts, Robert. Yes, ancient civilizations were far more advanced than many give them credit for in their understanding of mathematics, geometry and astronomy, and their passionate application of it in art and architecture. Their thinking was framed in a unified view of scientific and the spiritual perspectives that we have lost today. The same approach that led to the sacred geometries in the Great Pyramid and Parthenon could also have led to the site selections of Kaaba and other important sites. See my article on Kaaba at https://www.goldennumber.net/golden-ratio-of-earth/ as well.
Any support from Quran or Sunnah?
WHOA!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!1111
http://tallbloke.wordpress.com/2013/02/20/a-remarkable-discovery-all-solar-system-periods-fit-the-fibonacci-series-and-the-golden-ratio/
I believe God created everything in order
Very interesting. This challenges many materialistic views of science that claim the universe is an accidental happening
This is genius
Do you know golden point on earth!!
Yes, I’ve investigated this topic. There are actually many golden ratio points depending on where you start. See https://www.goldennumber.net/golden-ratio-of-earth/.
Makkah
i agree good tune
Your math is wrong. The hyporonuse of the triangle for the earth moon ratio is 10320 divided by 8114 is about 1.27 that’s .4 of from Phi.
You should really do the math here, and learn to see for yourself the wonders of this world.
Hello, Skeptic. The math is correct. The “about 1.27” you calculated represents the SQUARE ROOT of Phi, which is 1.2720 to four places. As the illustration shows, the 10320.77/8114.07 ratio corresponds to the hypotenuse of the triangle divided by its height. This is Phi divided by the square root of phi, which is the square root of phi, or 1.272.
Another way of looking at the relationship is to take 10320.77² / 8114.07², which is 106,518,293.39 / 65,838,131.96, which is 1.618.
I read a good quote recently. It said, “You should really do the math here, and learn to see for yourself the wonders of this world.” 🙂
You guys have no idea just how extensive the Φ ratio permeates the natural physical world! You’ve only scratched the surface with the mainstream information on that ratio.
Things start getting real interesting when you combine the 9 code with the Φ code!
For example:
When one performs the classic “squaring of the circle” exercise, you end up with the moon in a 3×3 box. The square of it’s diagonal = 3²+3², or 9+9. This of course is the number 18; which by the way = (Φ^6 + ¹/Φ^6)
Now you have everything you need to calculate six types of moon cycles and and one earth cycle to the typical accuracy of about 00.001% on most, a little larger margin on a few. (18, Φ≈1. 618, φ≈0.618)
Soros ≈ 18 years: (Φ^6 + ¹/Φ^6)
Node precession ≈ 18+φ years
Eclipse on same date ≈ 18+Φ-φ years
Eclipse year ≈ (18+φ)² days. ( 18+φ days short of a solar year).
12 full Moons ≈ (18+φ) (18+Φ-φ) days.
1 Solar Year ≈ (18+φ) (18+Φ) days.
13 full Moons ≈ (18+φ) (18+Φ²) days ( 18+φ days over a Solar year)
Those are some very interesting relationships, Vonnwolf. Keep them coming.
HOLY WOW.
thanks man, as an engineer, and math/physics/astronomy buff you have no idea how much this appeals to my spiritual side also.
“This of course is the number 18; which by the way = (Φ^6 + ¹/Φ^6)”
Several years late to the party. I noticed talk of Aten. That’s now spelled “Eighteen”.
Here’s another one you might find interesting:
We’re all familiar with how the Fibonocci Sequence approaches the Phi ratio with greater and greater precision as the sequence progresses, but did you know it’s embedded with the 9 code, and it’s on a numerical resonance frequencies of 24 with a half frequency demarcation at 12 (such as the twelve steps of Horus at day/night for a 24 hour day)? Example:
If you where to write out the Fibonocci Sequence from left to right, then right the numeric summation of each sequence under each sequence (just like you do for Gemotria); you’ll notice the number 9 only appears at every twelfth position, and the sequence of totals repeat themselves every twenty-four positions.
But now guess what? If you reright the summation sequence again under the first summation sequence, but shift the sequence by twelve positions and begin with sequence thirteen, you’ll
find that when you ad the top and bottom summation sequences to each other they all total to 9, every single one! you’ll just have a long row of never ending nines!
But what’s really interesting is that in reality all this is born out of the simple square; the Phi ratio, the sizes of all the rocky planets / moon, and much more.
Thanks. I cover this one at the Fibonacci 24 Repeating Pattern page.
Here’s a simple one. We all know that the mean tilt of the earth’s axis is approximately 23.3°, wobbling in sync with the Sun’s Sunspot Cycles ± 1.2°(going from memory) with our current angle at about 23.4°. Well, did you know that the Phi ratio is encoded in that too?
The earth’s axis mean tilt angle ≈ tan¯¹(Φ²+Φ¯²/Φ⁴+Φ¯⁴) = tan¯¹(3/7) ≈ 23.2°
And if you’re familiar with the “Squaring of the Circle” exsercise, You’ll recognize the significance of those right angle numbers with 7 being the distance between the moon and earth, and 3
being the diameter of the moon.
Interesting, and creative. We need a standard though by which to determine what qualifies as a meaningful relationship based on phi versus a creative way to get to a desired result. One of the unique qualities of phi is that Phi raised to any even integer plus the reciprocal of that number will result in an integer. That allows one to say that any integer in this series is related to Phi. Does that mean that the Earth’s axis tilt is actually based on Phi, or does it just mean that we can develop a formula to approximate that value using Phi?
As an analogy, we can divide 360° by Phi to get two sections of 222.5° and 137.5°. It’s said that plants arrange their leaves by this angle. The rationale is that this pattern results in the most sunshine to all leaves. Is there a rationale that would explain why the Earth’s tilt would be actually related to Phi as you’ve described? That would make it much more scientific and compelling as an explanation.
It would seem that the simpler and more obvious golden ratios in nature would be more meaningful than those that involve more complex formulas, wouldn’t you agree?
Dont forget the fine structure constant is 1/137 😉
Very interesting. This challenges many materialistic views of science that claim the universe is an accidental happening..
Of Course.
revelatory
Can we practically use Phi- the Golden Ratio to gain in our daily life? What are the daily things one can do to gain from this powerful revelation of Phi. So far we have been able to deduce mathematically but how can I use this in daily life?
I’ve answered this question on Quora in several different ways. See the posts here:
https://www.quora.com/What-are-some-applications-of-the-golden-ratio/answer/Gary-Meisner
https://www.quora.com/What-is-the-golden-ratio-and-where-is-it-used-in-our-day-to-day-life/answer/Gary-Meisner
https://www.quora.com/How-can-the-golden-ratio-help-me-in-my-daily-life/answer/Gary-Meisner
https://www.quora.com/How-do-I-use-the-Golden-Ratio-to-design-logos/answer/Gary-Meisner
https://www.quora.com/How-can-the-golden-ratio-or-the-Fibonacci-series-be-used-in-engineering-design-and-not-just-for-aesthetics/answer/Gary-Meisner
Is there any golden ratio with regard to the position of Earth in Solar System ?
Yes. See https://www.goldennumber.net/solar-system/ for more.
The following books will be eye openers to anyone reading them:
Adri de Groot, The Secret World of Numbers. Available on http://www.Lulu.com.
Richard Heath, The Matrix of Creation. St. Dogmaels: Bluestone Press, 2002.
Robin Heath, Sun, Moon, & Earth. New York: Walker & Company/Wooden Books, 1999.
John Martineau, A Little Book of Coincidence. New York: Walker & Company/Wooden Books, 2001.
Peter Plichta, God’s Secret Formula: Deciphering the Riddle of the Universe and the Prime Number Code. Rockport, MA: Element Books, 1997.
Using the Fibonacci scale versus distance of each planet from the Sun, one must consider the weight of the matter of each in the formula. Does anyone already have this calculation?
read the books by Richard Heath and his brother Robin Heath and you will see this in far greater details explained.
What about the golden spiral formed by tracking the moon in a lunar eclipse. I have an image I can mail you to indicate what I mean
So much to say here but I have so much to do.
Egyptian hieroglyphs of the “light bulbs” pointed towards one another…
Plasma bulbs emitting waves of Golden Proportions towards a center point.
The only proportion which matter can manifest from.
The pathway back to homeostasis as well as where we came from.
Are you ready for your mind to explode? Dont go down this rabbit hole unless you can step away from reality for a month.
Here you go….. Google “Dan Winter Golden Ratio Everything” 😀
Its the secret to everything….. soon us humans will be in sync with life’s dna and this code. We are just before the edge of the next dimension. Also aliens are on earth and always have been but they are just living in another dimension
another dimension? you think?
read the books by Richard Heath and his brother Robin Heath and you will see this in far greater details explained.
https://www.amazon.com/Sun-Moon-Earth-Wooden-Books/dp/0802713815
You guys have no idea just how extensive the Φ ratio permeates the natural physical world! You’ve only scratched the surface with the mainstream information on that ratio. https://www.guideadda.com/havells-max-ro-uv-water-purifier/
Do you even know Pythagoras’ theorem ?
Hypotenuse squared equals Opposite squared plus Adjacent squared.
So if the vertical is root phi and the horizontal is one the hypotenuse is root (phi + 1 )
Yes, the Pythagorean Theorem was used to derive and test the very close golden ratio relationship in the dimensions of the Earth and Moon. Based on your comment though, I see that it could have been presently more clearly and have made some improvements. Thank you for your feedback. Skeptic or not, the math does work to within 0.009% accuracy.
Thank you for your work.
I believe all of your math is correct or at most have some minor mistakes.
So, I have one question to ask. What do the “Mainstream” scientist say about these extremly rare coincidences?
To answer your question, one must first define what a “mainstream” scientist is. Scientists have a wide variety of fields of specialty, and a rare few have deep knowledge across all. Scientists have a wide range of world views, from atheists to theists, so that too influences the way the interpret the evidence. It’s more meaningful and important for each person to look at the evidence for themselves and to come to their own conclusions.
Wow, guys, amazing to the moon and back. Likely ancient celestial navigators understood these ratios better than today. Anti Kithera Greek clockmakers must have known these mathematical, astro-earth keys of pi and the golden ratio and incorporated them into a very practical application for navigators. Thank you for sharing your expertise. I’m still trying to wrap my head around it, (golden pi pun intended).
So taking it further into circadian rhythms and lunar effects on tides, migrations and conception/birthing cycles of fish, birds, animals and humans (it’s all been researched and shown to have correlations to solar seasons and lunar phases) – -from design/creation sequence and ratios of phases recorded in Gen. 1 – would like to hear your inputs.
And in Jubilees 2 (“Little Genesis”) there is a reference to [22 heads of mankind from Adam to Jacob] and 22 kinds of work made until the 7th day…. there’s the ratio of pi 22/7. Comments? Again, thank you.
I see I need to order some of your books.
Thanks, Joan. Here’s a link to purchase them on Amazon: https://bit.ly/goldenratiobook
Thanks, Joan. Here’s a link to the book on Amazon: https://bit.ly/goldenratiobook