What makes a single number so interesting that ancient Greeks, Renaissance artists, a 17th century astronomer and a 21st century novelist all would write about it? It's a number that goes by many names. This “golden” number, 1.61803399, represented by the Greek letter Phi, is known as the Golden Ratio, Golden Number, Golden Proportion, Golden Mean, Golden Section, Divine Proportion and Divine Section. It was written about by Euclid in “Elements” around 300 B.C., by Luca Pacioli, a contemporary of Leonardo Da Vinci, in "De Divina Proportione" in 1509, by Johannes Kepler around 1600 and by Dan Brown in 2003 in his best selling novel, “The Da Vinci Code.” With the movie release of the “The Da Vinci Code”, the quest to know Phi was brought even more into the mainstream of pop culture. The allure of “The Da Vinci Code” was that it creatively integrated fiction with both fact and myth from art, history, theology and mathematics, leaving the reader never really knowing what was truth and … More on Math, Myth and Truth
Featured Articles: Math or Myth? An overview and the evidence
Golden Ratio Myth, Fact and Misunderstanding: The missing evidence
There are many misconceptions and misrepresentations about the golden ratio. Some look too fervently for patterns and say it exists where it really doesn't. Some whose goal is to debunk golden ratio myth say it doesn't exist where it really does, missing the obvious and often not stating what proportions appear instead. People on both sides often just repeat what they've heard rather than personally performing the analysis required to support their conclusions. Intelligence and education are not always factors in getting to the truth, as even Ph.D.'s in mathematics sometimes get it wrong. As the author of this site since 1997, I've changed my views and the information on this site as well. Let's look at some of the common points of confusion and debate, covering beauty, the Parthenon, the UN Secretariat Building, the Great Pyramid, Nautilus shell, use by famous artists (Da Vinci, Botticelli, Seurat, etc.) and other topics. I'll provide objective answers, with additional evidence in the … More on Math, Myth and Truth
Gary Meisner’s latest Tweets on the Golden Ratio
Here are the latest Tweets on the golden ratio, Fibonacci sequence and related topics by Gary Meisner. Gary's qualifications include: Founder and author of the website GoldenNumber.net, Developer of PhiMatrix Golden Ratio Design and Analysis software and Author of the book "The Golden Ratio - The Divine Beauty of Mathematics:" Tweets by GaryBMeisner … More on Math, Myth and Truth
Latest blog articles
The World’s Most Beautiful Buildings, According to Science and the Golden Ratio
Abstract Several recent studies have attempted to rate the beauty of objects (cars, buildings) by mimicking an analysis technique created for facial analysis. While these efforts are very creative and involved a lot of work, they fail to produce reliable results for two reasons. First is that human faces have a common set of features that can measured against a standard, while the objects of the study do not. Second is that the studies did not actually measure golden ratios, which in geometry and visual aesthetics are based on dividing a line segment at its unique golden ratio point. The studies instead calculated the ratios of all possible permutations of two line segments created by each combination of three marker points. The object whose mathematical average of all the ratios came closest to the number 1.618... (or its reciprocal 0.618...) was declared "the most beautiful according to science and the golden ratio." Since the objects identified as the "most beautiful" by the … More on this article
The Science Channel Parthenon documentary features Gary Meisner as Golden Ratio Expert
If We Built It Today - Code of the Parthenon In April 2021, the Science Channel released an intriguing new documentary in their "If We Built It Today" series. In Episode 3 of Season 2, the "Code of the Parthenon" explores the wonders and mysteries of the Parthenon of ancient Greece, and contemplates what it would take to build it today. The show features experts in architecture, engineering, history, sculpture and more. For insights into the beauty, aesthetics and design of the Parthenon, show producer Andrew Killawee turned to Gary Meisner as his Golden Ratio expert. Gary is, of course, the founder of this site at GoldenNumber.net, developer of PhiMatrix Golden Ratio Design and Analysis software and author of "The Golden Ratio - The Divine Beauty of Mathematics." Gary knows from past experience that you never know what parts of a one or two hour interview are going to end up as the few quotes or sound bites that make it to the final cut of an article or documentary. This … More on this article
Golden Ratio Interview – December 2020
As the author of this website, I'm often asked by students doing science and math projects for assistance, including answering questions when they need to interview someone on the golden ratio. Here are some questions from Elena from Austria, who was working on her pre-scientific work as one part of her final exam to finish high school, along with my responses to her. She covered a variety of interesting topics regarding appearances and applications of the golden ratio, including phyllotaxis, identifying meaningful appearances, human attractiveness, the pyramids, art and future expectations and implications. More importantly, she asked questions on how one can know whether a claimed appearance of the golden ratio has validity, and what significance we should find when the golden ratio is found so frequently in nature. Occurrences of the Golden Ratio Phyllotaxis Pineapples: It is a well-known fact in mathematics that you can find the golden ratio and the Fibonacci-sequence on … More on this article
Applications for Better Art, Design and Composition
The Golden Ratios of the Parthenon
The Parthenon has long been associated with the golden ratio. The lack of clear evidence to support this though has led some to conclude in error that this is just a myth. This article will provide the best evidence I've found to date to illustrate appearances of golden ratios in the design of the Parthenon. In my analysis, I'll use the golden ratio grids created with pixel-level accuracy by my PhiMatrix software. These include golden rectangles and/or rectangles with a dividing line at the golden ratio point of their height or width. I'll apply these to the best photos and illustrations of the Parthenon available. This requires that the images be very high resolution, and taken from directly perpendicular to the Parthenon to avoid distortions from perspective. As a quick background, the golden ratio is defined by dividing a line at the one point at which the ratio of the larger segment (a) to the small segment (b) is equal to the ratio of the line (a+b) to the larger segment (a). Note … More on Art and Design
Carwow, best-looking beautiful cars and the golden ratio.
In November 2019, Samantha James of Carwow published a very interesting article titled "Best-looking cars of the last decade." What made it more interesting yet is that their review applied golden ratio analysis techniques used for human faces to the front end view of automobiles. Headlights became eyes. Emblems became noses. Grills became mouths. Makes good sense, right? I've been showing the golden ratio in human faces since the late 1990s. London plastic surgeon Dr. Julian Silva is recognized for giving a golden ratio score of famous celebrity faces, as shown below left. Carwow used a very similar approach, as shown on the right: Carwow is UK company that helps consumers to make choosing and buying their perfect car easy and enjoyable. Stefanie Finch of their PR agency, Propellernet.co.uk, contacted me on behalf of Carwow to ask if I'd be interested in covering their story on this site. I of course said "YES!" She and the Carwow team were kind enough to provide me with the … More on Art and Design
Golden Ratio, Phi and Fibonacci Commemorative Postage Stamps
Governments around the world commemorate the Golden Ratio, Phi and Fibonacci sequence. Stamp collecting is one of the world's most popular educational hobbies, and is enjoyed by people of all ages and nationalities. The most popular stamp ever is US 1993 Elvis stamp, with over 124 million collected. So, the Golden Ratio and Fibonacci sequence may not compete with Elvis in popularity anytime soon, but they too have been recognized with commemorative stamps issued by governments around the world. In addition to adding some "phi" to "philately," they offer some interesting expressions of golden ratio concepts, as well as its application in design. Liechtenstein 2013 Commemorative Fibonacci Sequence and Phi Stamp set: The Principality of Liechtenstein, a landlocked micro-state bordered by Switzerland and Austria, issued a set of three stamps in 2013 that illustrate the Fibonacci sequence and its relationship to the golden ratio. Note that interesting presentation of concepts: The first … More on Art and Design
The Golden Ratio in Character Design, Cartoons and Caricatures
The golden ratio is Stephen Silver's secret weapon of character design. Stephen Silver is a character designer and art teacher who has designed characters for Disney Television Animation, Sony Feature Animation and Nickelodeon Animation. In this role he has designed the style of the shows such as "Kim Possible", Kevin Smith's "Clerks" the animated series, "Danny Phantom" and many others. He is also the author and artist of seven books on the art of character design, caricature, sketching and life drawing. In addition to his freelance work and lectures, he owns an art school called Silver Drawing Academy in Simi Valley, CA. He has two online character design courses online at www.schoolism.com. Those are some great credentials. And what does he say is his "secret weapon" for character design? Yes, it's the golden ratio. The golden ratio is flawless because it gives the "small, medium and large" that design is built upon. He describes the golden ratio is just perfect, flawless, … More on Art and Design
Golden ratios in Great Pyramid of Giza site topography
Overview: Analysis of the site of the Great Pyramid of Giza reveals that the positions and relative sizes of the pyramids may be based on the golden ratio. Evidence of the Golden Ratio in the Great Pyramid complex. There are many pyramid theories and questions as to who built the pyramids in ancient Egypt. It's commonly known though in Egyptology that the proportions of the Great Pyramid of Egypt are within inches of a golden ratio-based pyramid. This is discussed in detail in my article Phi, Pi and the Great Pyramid. Some say, however, that this single piece of evidence is just a simple coincidence. The primary rationale given to deny this claim is that there is no written historical evidence that the ancient Egyptians had any knowledge of the golden ratio. That's a reasonable objection, but what if the evidence showed that the application of the golden ratio at Giza was not limited to the Great Pyramid? That evidence is presented in this article. The golden ratio connection … More on Art and Design
Michelangelo and the Art of the Golden Ratio in Design and Composition
New study unveils Michelangelo's extensive use of the golden ratio in the Sistine Chapel. In 2013, I reported that Michelangelo used the golden ratio in his painting "The Creation of Adam" in the Sistine Chapel. This Divine Proportion appears at the point at which Adam's finger is touched by the finger of God, as God breathes life into Adam. In July 2015, Clinical Anatomy published an article by a team from Brazil titled "More than a neuroanatomical representation in The Creation of Adam by Michelangelo Buonarroti, a representation of the Golden Ratio." (PDF here.) The article claimed, incorrectly, that there was no previous association of Michelangelo's works with the golden ratio. It identified the very same golden ratio touch point as the one reported here two years earlier. It also claimed, however, a new finding. It claimed that the fingers touched at the golden ratio point of the length of all the paintings on the ceiling of the Sistine Chapel. My analysis of this claim … More on Art and Design
Google Logo and the Golden Ratio in Design
New Google logo design finds visual harmony using the Golden Ratio. Google's design follows in the footsteps of Leonardo da Vinci and other masters When Luca Pacioli published "The Divine Proportion" in 1509 (with illustrations by Leonardo da Vinci), he described his work on this "golden ratio" of 1.618 as a "very delicate, subtle and admirable teaching" that would "delight in diverse questions touching on a very secret science." Johannes Kepler later called it "a precious jewel" of geometry. The designers at Google have apparently found its value too, as we see when we study and appreciate the underlying design of Google's new logo, iconic G, the microphone icon and even the layout of the Google search page. This is the kind of thoughtful design work that follows in the footsteps of Leonardo, Michelangelo, Raphael, Botticelli, Seurat, Le Corbusier and other masters of design, and that would make Pacioli proud. Here's a version without the arrows for a clearer … More on Art and Design
Raphael and the Golden Ratio in Renaissance Art
Raphael was one of three Master artists of the Renaissance Raffaello Sanzio da Urbino, known as Raphael, was an Italian painter and architect of the High Renaissance and lived from 1483 to 1520. He is recognized as one of the three great masters of that period, accompanied by Michelangelo and Leonardo da Vinci. His work is admired for its form, composition, and visual achievement of the ideal of human grandeur. One of his most famous works is The School of Athens, a fresco in the Apostolic Palace in the Vatican. It captures the spirit of the Renaissance, and is revered as his masterpiece. It was painted between 1509 and 1511. The School of Athens: Inspired by a union of art and mathematics It was also in 1509 that Luca Pacioli published the book De Divina Proportione (The Divine Proportion), with illustrations by Leonardo da Vinci. MonaLisa.org reports that The School of Athens "incorporates many of the mathematical theories of Luca and Leonardo." "Civilisation" author Kenneth … More on Art and Design
Stock Market and FOREX Trading Analysis
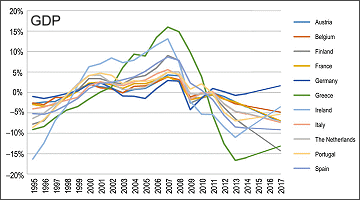
GDP growth subcycles and the Golden Ratio
In 2021, Bert de Groot, Professor of Governance and Strategic Investment Policy at Erasmus School of Economics, published a paper in “Technological Forecasting and Social Change” titled “Disentangling the enigma of multi-structured economic cycles - A new appearance of the golden ratio.” In his paper, De Groot examines the economic cycles of GDP growth in over two dozen countries. He found that their durations are grounded in golden ratio relationships. De Groot took an empirical approach to chart a pattern in the lengths of sub-cycles in GDP growth. Understanding the interrelationships between the length of economic sub-cycles then allows their cycles and their fluctuations to be detected … More on Markets/Gaming
Phi and Football Strategy’s Golden Ratio Rule
Using the Golden Ratio to win at football. The golden ratio is found in many places, but here's one you might not have expected: It can be found in football gaming strategy when making the "point after touchdown" decision as to whether to kick for 1 extra point or go for a 2 point conversion. This applies to the situation when a team is trailing by 14 points late in a football game, and then scores a touchdown to be trailing the other team by 8 points. So what should you do: Kick for 1 point after touchdown (PAT) or go for a 2 point conversion? Most football teams kick the PAT in this situation, but in fact it is (almost) always better to go for 2. The reason is related to … More on Markets/Gaming
What determines our perceptions of beauty?
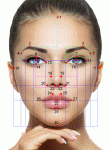
Meisner Beauty Guide for Golden Ratio Facial Analysis
Facial golden ratios are simple, clear and abundant. Since my first investigation of human facial proportions in 1997, it seemed clear that the most important features that define a human face are the simplest and most obvious: An oval head and the positions and dimensions of the eyes and the mouth. As evidence, consider the "smiley face." It expresses a variety of facial expressions with nothing more than a circular head, two eyes and a mouth line: We immediately recognize this icon as a face, but it clearly does not represent the proportions of a human face. Let's instead express these same facial markers with normal human proportions, and with the simplest possible representation. This requires a vertical oval, two lines for the eyes and a line for the mouth. The resulting face will look something more like this: This simple facial configuration is easily mapped to very natural human proportions with the use of four simple golden ratio proportions: The next important human facial … More on Beauty
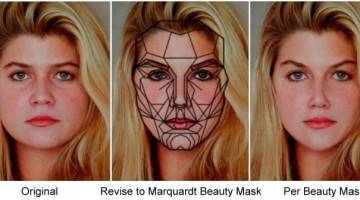
Facial Analysis and the Marquardt Beauty Mask
A template for human beauty is found in phi, the pentagon and dodecagon Dr. Stephen R. Marquardt is the world's most recognized expert on facial analysis and beauty. He has appeared in many documentaries and been referenced in countless articles, including the Beauty episode of BBC's 2001 documentary "The Face." Dr. Marquardt, also CEO of Marquardt Aesthetic Imaging, has studied human beauty for decades in his practice of oral and maxillofacial surgery, and now continues his studies full time. His work includes cross-cultural surveys on beauty, in which he found that all groups had the same perceptions of facial beauty. He also analyzed the human face from ancient times to the modern day. Through his research, he discovered that beauty is not only related to phi, but can be defined for both genders and for all races, cultures and eras with the beauty mask which he developed and patented. This mask uses the pentagon and decagon as its foundation. Both of these geometric shapes embody … More on Beauty
The Human Face and the Golden Ratio
The human face is based on Phi and Golden Ratio proportions. The human face abounds with examples of the Golden Ratio, also known as the Golden Section or Divine Proportion. We'll use a succession of golden ratios to create a golden ruler to understand design in the face: The head forms a golden rectangle with the eyes at its midpoint. The mouth and nose are each placed at golden sections of the distance between the eyes and the bottom of the chin. The beauty unfolds as you look further. Even when viewed from the side, the human head illustrates the Divine Proportion.The first golden section (blue) from the front of the head defines the position of the ear opening. The successive golden sections define the neck (yellow), the back of the eye (green) and the front of the eye and back of the nose and mouth (magenta). The dimensions of the face from top to bottom also exhibit the Divine Proportion, in the positions of the eye brow (blue), nose (yellow) and mouth … More on Beauty
Beauty, the perfect face and the Golden Ratio, featuring Florence Colgate
What determines the beauty of a perfect face? We may never answer the question "how many angels can dance on the point of a needle," but how about this one: "How many Divine proportions ratios are there in the face of an angel?" The YouTube video and information in this article may give some insight into the answer, with details on the contest, a recap of explanations of beauty that fall short and new insights and a video illustrating the impact of the golden ratio in beauty. The British contest in 2012 to find "Britain's Perfect Face" draws over 8,000 entries, and finds Florence Colgate as the winner British company Lorraine Cosmetics sponsored a contest in 2012 to find “Britain’s Perfect Face.” Billed as the "Naked Competition," and seeking the most perfect makeup-free face, contestants were required to have completely natural faces, without make-up, botox or cosmetic surgery. The competition drew entries from 8,045 contestants, who were initially screened by a panel that included … More on Beauty
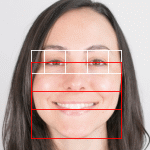
The Golden Ratio, Beauty and Design: It’s time to ‘face’ the facts.
Another attempt to debunk the Golden Ratio is fundamentally wrong. In October 2015, Dr. Keith Devlin was interviewed by science writer Julia Calderone in an article titled "The one formula that's supposed to 'prove beauty' is fundamentally wrong." Professor Devlin is a accomplished Ph.D. in mathematics at Stanford University and NPR's Math Guy. His comments have reach and impact, but his views on the golden ratio are not always accurate, complete, consistent, objective or supported by evidence. Earlier in 2015, he was featured by a leading online design magazine in an article titled "The Golden Ratio: Design’s Biggest Myth – The Golden Ratio is Total Nonsense in Design. Here’s Why." The article drew hundreds of negative responses (which were later censored and deleted by the magazine) because of its inaccuracies and misrepresentations. A highly regarded NYC designer, Darrin Crescenzi, described the article as "dangerous" and "under-informed nonsense," motivating him to write a … More on Beauty
How to take photos and measurements for facial beauty analysis and identification of golden ratio proportions
Best practice techniques for facial and beauty analysis. Numerous studies have been done to investigate the existence and/or relationship of golden ratio proportions in the human face. Surprising few get it right, so the results of many of these studies are inaccurate and misleading. There are four important keys to selecting photographs that are suitable for facial measurements. Next, it is critical to understand and measure the facial markers that commonly reflect golden ratio proportions. In this article I'll cover these key points, the common mistakes made and the best practices to yield results that are both accurate and meaningful. 1. Orientation of the head, and eliminating the impacts of perspective. As simple as it sounds, one of the most important aspects of any image used for facial analysis is that the subject be looking directly into the camera. The front of the face must be parallel to the lens of the camera. There must be no tilt of the head either up, down, left or … More on Beauty
Appearances in Life and Nature
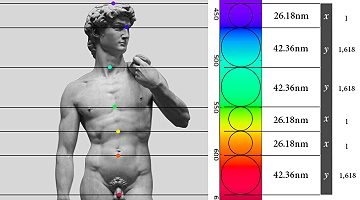
Light, the Human Body, Chakras and the Golden Ratio
Kalana Dido of France made a very insightful discovery in May 2021 that unites the visual spectrum of light, the proportions of the human body, the chakras (i.e, the centers of spiritual energy in the human body in Hindu tradition) and the Golden Ratio. This integrates four separate concepts, making it one of the more fascinating discoveries of Golden Ratio appearances I've seen in recent years. Let's explore each topic and then see how they then relate. The Visual Spectrum of Light Most people know the familiar colors of the rainbow and the visual spectrum of light as red, orange, yellow, green, blue, indigo and violet. This is often referred to by the acronym "ROYGBIV": Have you ever noticed though that the individual ROYGBIV colors we readily distinguish are not evenly dispersed across the spectrum? Some colors are tightly grouped within a small range of wavelengths and frequencies. Other colors spread across a wider band. Keep that thought. Chakras and the Human … More on Nature
Is the Nautilus shell spiral a golden spiral?
Nautilus shell spirals may have phi proportions, but not as you may have heard. The Nautilus shell if often associated with the golden ratio. There is a fair amount of confusion, misinformation and controversy though over whether the graceful spiral curve of the nautilus shell is based on this golden proportion. Some say yes, but offer no proof at all. Some show examples of spirals, but incorrectly assume that every equi-angular spiral in nature is a golden spiral. Several university math professors say no, but they only compared the nautilus spiral to the spiral created from a golden rectangle. Another university professor says no, but only measured height and width of the entire shell. Let's look at this objectively and solve this mystery and debate. The Golden Spiral constructed from a Golden Rectangle is NOT a Nautilus Spiral. A traditional Golden Spiral is formed by the nesting of Golden Rectangles with a Golden Rectangle. This resulting Golden Spiral is often associated with … More on Nature
Appearances in the Cosmos
Quantum Gravity, Reality and the Golden Ratio
What if the belief that the golden ratio is a foundational building block of the universe turned out to be true? Long thought to be the fodder of mystics and cranks, it now appears that once was thought to be myth may in fact be at the center of the math that defines reality as we know it. Quantum Gravity Research (QGR) is a research organization which states its mission as: "QGR’s mission is to discover the geometric first-principles unification of space, time, matter, energy, information … More on the Cosmos
Stars that Pulsate to the Golden Ratio
A research article called "Strange Nonchaotic Stars" published at the American Physical Society reported the discovery of a class of white-blue variable stars that pulsate in a fractal pattern at frequencies close to the golden ratio. Download the paper in PDF format here: strange-nonchaotic-stars-pulsate-golden-ratio-1501.01747v2 Pulsations described as "strange nonchaotic behavior." The discovery was reported by John F. Lindner, Vivek Kohar, Behnam Kia, Michael Hippke, John G. Learned, and … More on the Cosmos
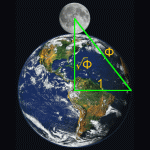
Phi and the Solar System
The dimensions of the Earth and Moon are in Phi relationship, forming a Triangle based on 1.618. The illustration shows the relative sizes of the Earth and the Moon to scale. Draw a radius of the Earth (1). Draw a line from the center point of the Earth to the center point of the Moon (square root of Phi). Draw a line to connect the two lines to form a Golden Triangle (Phi). Using dimensions from Wikipedia and geometry's classic Pythagorean Theorem, this is expressed mathematically as … More on the Cosmos
Unique Properties in Geometry
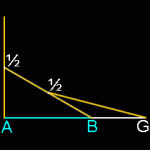
Phi and Geometry
Phi (Φ) was described by Johannes Kepler as one of the "two great treasures of geometry." (The other is the Theorem of Pythagoras.) Phi appears in many basic geometric constructions. 3 lines: Take 3 equal lines. Lay the 2nd line against the midpoint of the 1st. Lay the 3rd line against the midpoint of the 2nd. The ratio of AG to AB is Phi, the Golden Ratio. (Contributed by Jo Niemeyer) 3 sides: Triangle Insert an equilateral triangle inside a circle, add a line at the midpoint of the two sides and extend that line to the circle. The ratio of AG to AB is Phi. 4 sides: Square Insert a square inside a semi-circle. The ratio of AG to AB is Phi. 5 sides: Pentagon Insert a pentagon inside a circle. Connect three of the five points to cut one line into three sections. The ratio of AG to AB is Phi. When the basic phi relationships are used to create a right triangle, it forms the dimensions of the great pyramids of Egypt, with the geometry shown below creating an angle of 51.83 … More on Geometry
